Mech-Slobod

Результатом дії оператора градієнта на поле деякої скалярної величини є вектор, який називають градієнтом цієї величини. Можна показати, що градієнт вказує напрям

найшвидшого зростання величини скалярного поля.

Отже, до частинки, що знаходиться в потенціальному полі, з боку цього поля

прикладена сила, що дорівнює градієнту потенціальної енергії частинки в точці її знаходження, взятому зі знаком мінус.

5.2.3. Повна механічна енергія частинки

Сили, прикладені до частинки, в загальному випадку завжди можна розділити на консервативні або потенціальні та неконсервативні або сторонні. Відповідно до (5.18) сумарна робота цих сил змінює кінетичну енергію частинки:

Величина E = T +U , сума кінетичної та потенціальної енергії частинки, називається

повною механічною енергією частинки,

З означення (5.49) видно, що повна механічна енергія частинки є функцією механічного стану частинки.

Умови зміни та збереження повної механічної енергії частинки. Відповідно до рівняння (5.48) приріст повної механічної енергії частинки на елементарному переміщенні дорівнює елементарній сумарній роботі всіх сторонніх сил,

152

а на скінченному переміщенні

де A12стор є сумарна робота всіх сторонніх сил на шляху між точкою 1 і точкою 2.

Оскільки

то повна механічна енергія частинки E змінюється, якщо сумарна потужність сторонніх сил

N стор , прикладених до частинки в кожен момент часу відмінна від нуля. Якщо N стор > 0 , то

повна механічна енергія частинки E зростає, а якщо N стор < 0 , то зменшується. Відповідно,

приріст повної механічної енергії частинки на деякому шляху дорівнює алгебраїчній сумі робіт

Aстор всіх сторонніх сил, що діють на частинку на цьому шляху: якщо Aстор > 0 , то повна

механічна енергія на цьому шляху зростає, а якщо Aстор < 0 , то зменшується.

З рівнянь (5.50) та (5.52) випливає умова збереження повної механічної енергії частинки:

повна механічна енергія частинки зберігається, якщо сумарна потужність або робота всіх

сторонніх сил, що прикладені до частинки, дорівнює нулю.

Якщо сторонні сили взагалі відсутні, то їх потужність у правій частині рівняння (5.52)

завжди дорівнює нулю. Тоді справедливий закон збереження повної механічної енергії

частинки:

Повна механічна енергія частинки, на яку не діють сторонні сили, зберігається,

тобто

5.2.4. Одновимірний рух частинки в потенціальному полі

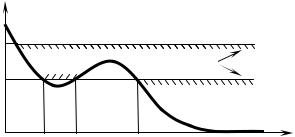
У демонстраційному досліді частинка (невелика сталева кулька) рухається по плоскій траєкторії, що лежить у вертикальній площині і проходить на різній висоті h над поверхнею демонстраційного стола (котиться вздовж направляючої, виготовленої з кутника) (Рис. 5.8).

Потенціальна енергія кульки в однорідному полі сили тяжіння є U (x) = mgh(x) , де h(x) −

висота кульки над поверхнею стола в точці з координатою x , яка відлічується вздовж поверхні

153

стола від початку направляючої, де її висота максимальна На направляючій є неглибокий мінімум на відстані порядку 1 м від початку (на Рис. 5.8 обрано різний масштаб по горизонталі

консервативної сили тяжіння кулька почне рухатись і її кінетична енергія буде зростати за рахунок роботи цієї сили, а потенціальна енергія − спадати. Оскільки опір руху кульки при її коченні є дуже малий (так званий коефіцієнт тертя кочення набагато менший за коефіцієнт тертя ковзання), а опір повітря при малих швидкостях також незначний, то на невеликих проміжках часу можна вважати, що повна механічна енергія кульки зберігається, E = const .

Тому після проходження мінімуму між точками x1 та x2 потенціальна енергія частинки

починає зростати, а кінетична − зменшуватись і, відповідно, зменшуватись швидкість. Після

проходження максимуму між точками x2 та x3 потенціальна енергія частинки знову

зменшується, а кінетична зростає, оскільки повна енергія частинки залишається сталою. Рух кульки можливий лише на тих ділянках, де кінетична енергія додатна, тобто при

оскільки швидкість має бути дійсною величиною. Ділянки, де E < U (x) є недосяжними для механічного руху. У зв’язку з цим, одновимірний рух може бути інфінітним, коли частинка прямує на нескінченність (у нашому випадку кулька може котитися по поверхні стола у напрямку необмеженого збільшення x ), або фінітним, коли частинка не виходить за межі

деякої ділянки між x1 > −∞ та x2 < ∞ , де виконується умова E ≥ U (x) . Для ходу

потенціальної енергії U (x) , зображеного на Рис. 5.8, фінітний рух може мати місце поблизу

154

мінімуму потенціальної енергії між точками x2 та x3 для значень повної механічної енергії

E2 , що є більші за величину потенціальної енергії U (xmin ) в мінімумі при xmin , x2 > xmin > x1 ,

але менші за величину потенціальної енергії U (xmax ) в максимумі при xmax , x3 > xmax > x2 ,

U (xmax ) > E2 > U (xmin ) . При таких енергіях E2 частинка може рухатись лише вперед-назад в

околі згаданого мінімуму потенціальної енергії, але не може подолати так званий

потенціальний бар’єр, утворений максимумом потенціальної енергії U (xmax ) , і перейти в

область, де можливий інфінітний рух (Рис. 5.8).

Цей дослід є демонстраційним і покликаний показати на якісному рівні основні риси одновимірного руху частинки. Якби кулька не котилася по направляючій, а ковзала по ній, то її повну механічну енергію можна було б подати як

= mυ 2 (x) +

E mgh(x) , (5.55)

2

звідки зразу видно, що швидкість кульки υ зменшується при збільшенні висоти h , що можна спостерігати, коли кулька долає потенціальний бар’єр.

Оскільки υ 2 = x2 + y2 , а похилі ділянки направляючої мають невелику крутизну, можна

Рівняння (5.54) описує так званий одновимірний рух частинки, при якому механічний стан частинки визначається лише однією змінною (координатою), що залежить від часу.

Зауважимо, що при чистому коченні однорідної кулі маси m зі швидкістю υ її кінетичну енергію можна знайти як суму кінетичної енергії її поступального руху зі швидкістю υ та кінетичної енергії її обертового руху з кутовою швидкістю ω = υ / r , де r − радіус кульки. Розрахунок показує (див. Вправу __

до Розділу 6), що кінетична енергія однорідної кулі, що котиться з швидкістю υ , є 0,9mυ 2 , а не 0,5mυ 2 , як це має місце у випадку, коли вона ковзає з тією ж швидкістю, але залишається пропорційною добутку маси на квадрат швидкості. Це означає, що рух кульки при коченні якісно залишається таким самим як і при

155

ковзанні, але відбувається дещо повільніше (в 1,34 рази), що для демонстраційного досліду навіть становить

певну перевагу.

Розглянемо приклад руху частинки в однорідному полі сили тяжіння по замкненому контуру.

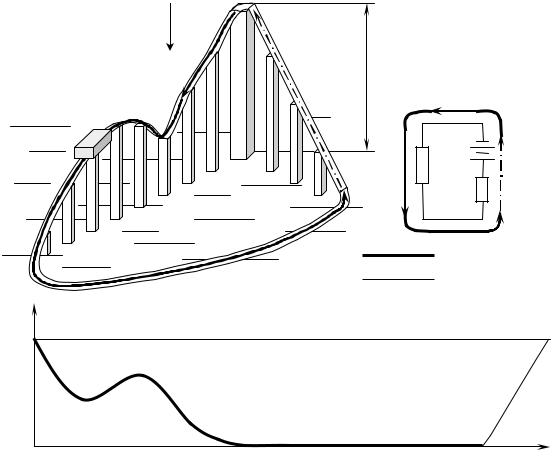
На Рис. 5.9а схематично зображено атракціон, який іноді називають «американські гірки». Нехай з вершини вежі висотою h починає рухатись по рейкам, що утворюють замкнений шлях 123451,

візок (на рисунку він схематично зображений як прямий паралелепіпед). На Рис. 5.9б показано профіль шляху візка. На ділянці шляху 1-4 потенціальна енергія візка зменшується, а кінетична збільшується за рахунок роботи консервативної сили тяжіння. На горизонтальній ділянці 4-5 візок

рухається по інерції. За відсутності дисипативних сил візок мав би досягнути точки 5 і почати підйом по похилій ділянці 51, на якій виконується робота проти консервативної сили тяжіння,

внаслідок чого зменшується кінетична енергія візка, а натомість зростає його потенціальна енергія,

яка на вершині вежі досягає свого початкового значення. В принципі, за відсутності сил опору візок міг би рухатись по замкненому рейковому шляху як завгодно довго. Але в дійсності на кожній ділянці траєкторії візок виконує роботу проти дисипативних сил (опір повітря, тертя кочення та інші). Крім того, на горизонтальній ділянці шляху 4-5 візок спеціально гальмують до повної зупинки, щоб у точці 5 приєднати до нього трос, за допомогою якого здійснюють підйом візка на вершину вежі. При цьому до візка з боку троса прикладено сторонню силу натягу, яка виконує роботу як проти консервативної сили тяжіння та дисипативних сил тертя. Отже, рух частинки (в нашому випадку візка) в потенціальному полі по замкненому контуру за наявності дисипативних сил можливий лише за рахунок сторонніх сил, які компенсують втрати кінетичної енергії частинки на роботу проти дисипативних сил. На Рис. 5.9а жирною лінією відмічено

ділянку шляху 1-5, на якій візок рухається за рахунок роботи консервативної сили Aконс , яка була виконана при зміні висоти від h до 0, а штрих-пунктирною лінією відмічено ділянку 5-1, на якій візок рухається виключно за рахунок роботи зовнішньої сторонньої недисипативної сили

Aстор недисип . При цьому від’ємна робота дисипативних сил виконується на будь-якій ділянці шляху.

Аналогічно відбувається рух електричного заряду по замкненому провідному контуру

(Рис. 5.9в). У так званій зовнішній ділянці кола рух електричного заряду, наприклад, електрона відбувається за рахунок роботи консервативних сил з боку потенціального електричного поля, яке

156

створюється в цій ділянці додатно та від’ємно зарядженими полюсами джерела електрорушійної сили (е.р.с.). Для перенесення електрона від додатно зарядженого полюсу до від’ємно

зарядженого полюсу джерела е.р.с всередині самого джерела, необхідні сторонні

(неконсервативні) сили, які будуть виконувати роботу проти сил потенціального електричного поля. Походження цих сил може бути різним: найчастіше це сили з боку вихрового електричного

(непотенціального) поля, яке виникає в електрогенераторах при змінах магнітного поля

(електромагнітна індукція), або так звані «хімічні» сили в гальванічних елементах та акумуляторах. Робота дисипативних сил, при переміщенні заряду вздовж контуру призводить до

Рис. 5.9

зовнішнього кола буквою R , а так званий внутрішній опір джерела е.р.с. буквою r . Для чіткого розуміння природи е.р.с., яку означають як фізичну величину, що у замкненому провідному контурі дорівнює роботі сторонніх сил по переміщенню одиничного заряду вздовж усього

157

контуру, уявимо, що джерело е.р.с. подібне до плоского конденсатора і складається з двох великих плоских обкладинок, з розмірами порядку розмірів стін аудиторії і з такою ж відстанню між ними.

Ми знаходимось між цими обкладинками і маємо задачу переносити на обкладинку «−»

негативні заряди, що прибувають на обкладинку «+» після їх переміщення по зовнішній ділянці контуру під дією консервативної сили з боку електростатичного потенціального поля. Ми можемо, в принципі, переносити ці заряди в руках, можемо навантажувати їх на візок і перетягувати його до обкладинки «−» тощо. Останній спосіб дуже подібний до методу піднімання

візка на вершину вежі у прикладі з американським гірками: заряди переміщуються від «+» до «−»

за рахунок роботи сторонніх сил (нашої мускульної сили, сили тяги, прикладеної до візка,

навантаженого негативними зарядами) яка йде на збільшення потенціальної енергії цих зарядів і на виконання роботи проти дисипативних сил (наприклад, сил тертя, що діють на візок). Наявність останніх на електричній схемі Рис. 5.9в уособлює внутрішній опір джерела е.р.с. r . Отже, з

точки зору механіки, немає принципової різниці між рухом візка по замкненій траєкторії у потенціальному полі сили тяжіння (Рис. 5.9а) і рухом електричного зарядка по замкненому контуру (замкненій траєкторії).

Зауважимо, що у випадку електричного кола існує можливість виключити дисипативні сили

(усунути електричний опір) і реалізувати багаторазовий обхід зарядом замкненого контуру без участі сторонніх сил, тобто здійснити тривале протікання струму по замкненому контуру, в якому відсутнє джерело е.р.с. Така можливість завдячує явищу надпровідності (зникненню електричного опору провідників при їх охолодженні до певної критичної температури) і має широке практичне застосування в так званих надпровідних соленоїдах, що широко використовуються в фізичному експерименті.

Соленоїд з матеріалу, здатного переходити в надпровідний стан, під’єднують до джерела е.р.с.,

встановлюють у ньому струм певної величини, охолоджують його нижче критичної температури,

замикають соленоїд накоротко надпровідником і від’єднують джерело е.р.с. Після цього струм може годинами циркулювати по замкненому надпровідному колу, яке складається лише з надпровідного дроту і не містить ніяких джерел е.р.с.

5.3. Закони збереження для системи частинок

Перейдемо до заключного етапу реалізації накресленого на початку цього розділу

плану: до з’ясування умов, при яких будуть зберігатися (залишатися незмінними в процесі

158

руху) введені нами адитивні величини, що характеризують механічний стан системи як цілого,

а саме :

імпульс системи частинок

i=1

5.3.1 Умови зміни та закон збереження імпульсу системи частинок

Умови зміни та збереження імпульсу системи частинок будемо шукати так само як і для однієї частинки. Візьмемо похідну за часом від імпульсу системи частинок і, з врахуванням другого закону Ньютона для кожної частинки, отримаємо

i=1

частинки системи. Але в загальному випадку i -та частинка системи може взаємодіяти як з іншими частинками системи, так і з матеріальними об’єктами, що не належать до системи частинок. Відповідно, сили, що прикладені до частинок системи, можна поділити на так звані

внутрішні, тобто сили взаємодії між частинками самої системи, і зовнішні, тобто сили взаємодії частинок системи з матеріальними об’єктами, що не належать до системи. Наприклад,

для i -тої частинки

Отже, умови зміни та збереження імпульсу системи частинок такі:

Імпульс системи частинок змінюється, якщо сума зовнішніх сил, прикладених до частинок системи відмінна від нуля;

Імпульс системи частинок зберігається (залишається сталим), якщо сума зовнішніх сил, прикладених до частинок системи дорівнює нулю.

Векторне рівняння (5.66) можна спроектувати на орти деякої системи координат. Тоді для

звідки випливає, що коли деяка компонента суми зовнішніх сил, прикладених до частинок

системи дорівнює нулю, то відповідна компонента вектору імпульсу системи частинок

зберігається.

Умова збереження імпульсу системи частинок, яка полягає у рівності нулю суми зовнішніх сил прикладених до частинок може задоволена або внаслідок взаємної компенсації зовнішніх сил або, коли зовнішні сили взагалі відсутні, як це буває у випадку так званих

замкнених (або, як іноді кажуть, ізольованих) систем частинок, що посідають особливе місце в механіці.

Систему частинок називають замкненою, якщо відсутня взаємодія частинок системи

з матеріальними об’єктами, що не належать до цієї системи.

Відсутність такої взаємодії означає, що на частинки системи не діють зовнішні сили,

Це означає, що для замкненої системи частинок сума зовнішніх сил у правій частині

рівняння (5.66) завжди і безумовно дорівнює нулю: F зовн ≡ 0 .

Закон збереження імпульсу системи частинок:

Імпульс замкненої системи частинок є величина стала,