УМК

Произведем тождественные преобразования в фигурных скобках, обозначив

Подставляя полученный результат в (1.282), получаем

0 < x < a , 0 < y < b

и двум парам граничных условий

Последние условия (1.289) обеспечивают непрерывность граничной функции в вершинах прямоугольника.

Не нарушая общности, можно предположить, что все ее значения в (1.289) равны нулю, т.к. к этому случаю можно привести любую задачу. Для этого надо представить решение в виде

D = 1 {[ϕ(a) − ϕ(0)]− [f (a) − f (0)]}.

ab

Для функции v(x, y) получим задачу Дирихле при нулевых значениях в вершинах прямоугольника. Итак, будем решать задачу (1.286) – (1.289), предполагая, что все значения в (1.289) есть нули.

Представим решение в виде

Удовлетворим теперь граничным условиям (1.294), которые содержат заданные произвольные функции

должны являться коэффициентами разложения функций соответственно f (x ) и

ϕ(x)

a

Подстановка этих значений постоянных A n и Bn в (1.299) приводит функцию u 2 (x, y) после несложных преобразований к виду

b

где

Окончательное решение задачи: u(x, y) = u1 (x, y) + u 2 (x, y).

1.39 ЗАКЛЮЧЕНИЕ

Сделаем некоторые общие замечания относительно области применения метода разделения переменных. В основе применимости метода лежит линейность как самих дифференциальных уравнений, так и краевых условий. Коэффициенты исходных дифференциальных уравнений должны быть постоянными либо представляться в виде функций, каждая из которых содержит лишь одну из переменных (такие уравнения нами были исключены из рассмотрения). Краевые условия должны быть однородными. Если в исходной задаче они неоднородны, то надо привести их к однородным. Метод Фурье использует технику разложения искомого решения по собственным функциям. Метод приводит к цели, если только удастся найти подходящую для заданных границ систему координат, допускающую разделение переменных в рассматриваемом уравнении. В случае двумерных задач граница рассматриваемой области должна состоять из координатных линий (в трехмерных задачах – из координатных плоскостей). Если используется декартова система координат, то границы области – отрезки прямых, параллельных осям координат (куски плоскостей, параллельных координатным плоскостям); при использовании полярной системы координат границы области

– дуги окружностей с центрами в полюсе и отрезки лучей, выходящих из полюса, и.т.д.

Эти обстоятельства сильно ограничивают применимость метода Фурье. Есть множество задач, где разделение переменных не удается либо потому что граница тела достаточно сложна, либо потому что коэффициенты в исходном дифференциальном уравнении не являются постоянными, либо потому что уравнение не является линейным. Поэтому разработаны и другие методы решения задач математической физики, такие, например, как метод конечных разностей, метод интегральных уравнений, метод Ритца-Галеркина, метод физического моделирования, рассмотрение которых выходит за рамки настоящего курса.

вует, и притом единственное, решение y = ϕ(x) уравнения y′ = f (x, y), опре-

деленное в некотором интервале, содержащем точку x 0 .

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т.е. в любой окрестности каждой точки (x; y) особого решения существует по крайней мере две интегральные кри-

вые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального

уравнения ни при каких значениях произвольной постоянной C ( в том числе и при C = ±∞ ).

С геометрической точки зрения особое решение есть огибающая семейства интегральных кривых (если она существует), т.е. линия, которая в каждой своей точке касается, по меньшей мере, одной интегральной кривой.

Например, общее решение уравнения y′ = ±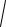1 − y2 записывается в ви-

де y = sin(x + C), − ∞ < C < ∞ . Это семейство имеет две огибающие: y = 1

и y = −1, которые будут особыми решениями данного уравнения.

2.2 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С РАЗДЕЛЕННЫМИ И РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

Дифференциальное уравнение y′ = f(x, y) называется уравнением с разделяющимися переменными, если его правая часть есть произведение двух функций, одна из которых зависит от y , а другая от x . y′ = f (x) g(y).

Предположим, что функции f (x) и g(y) непрерывны на интервале a < x < b, c < y < d и что g(y)≠ 0 .

Умножая обе части уравнения y′ = f (x) g(y) на dx и деля на g(y), за-

пишем его в виде: dy( ) = f (x)dx . g y