93

Теорема 3 (о промежуточном значении). Пусть функция

f (x) не-

прерывна на отрезке a; b и max

f (x) M ,

min

f (x) m . Тогда для лю-

x a ; b

x a ; b

бого числа c m; M существует x a; b такое, что f (x) c .

X

Y

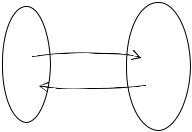
Определение 3. Пусть

дана

функция

y f (x) . Тогда обратной функцией для

f (x)

f (x)

называется функция f 1( y) : для любого

y Y

x

y

выполняется f 1( y) x , где f (x) y

(рис. 3.19).

f 1( y)

Теорема 4.

Пусть функция f

(x) опреде-

Рис. 3.19

лена и непрерывна на отрезке a; b и является

на всем этом отрезке либо возрастающей функ-

цией, либо убывающей. Тогда обратная функция x f 1( y)

будет непрерыв-

ной на отрезке c; d

, где c; d – множество значений функции

f (x) .

Доказательство.

f (x x) g(x x) f (x) g(x)

f (x) g(x)

lim

x

x 0

lim

f (x x) g(x x)

f (x) g(x) g(x x) f (x) g(x x) f (x)

x 0

x

lim

g(x x) ( f (x x)

f (x))

lim

f (x) (g(x x) g(x))

x

x 0

x 0

x

lim

f

lim

g

g(x x)

x

f (x)

x

g(x) f (x) f

(x) g (x) .

x 0

x 0

Теорема 3. Пусть

функции

f (x) ,

g(x) дифференцируемы. Тогда

функция

f (x)

будет дифференцируема (там, где она существует) и

g(x)

f (x)

f (x) g(x)

f (x) g (x)

.

g

2

(x)

Доказательство.

g(x)

f (x x)

f (x)

f (x)

lim

g(x x)

g(x)

g(x)

x 0

x

lim

g(x) f (x x) f (x) g(x x) f (x) g(x) f (x) g(x)

x 0

g(x) g(x x) x

g(x) f f (x) g

lim

f

g(x) f (x) lim

g

lim

x 0 x

x 0

x

x 0

x g(x) g(x x)

g(x) lim g(x x)

x 0

g(x) f (x) f (x) g (x)

.

g 2 (x)

19.3

Производная сложной функции

Теорема.

Пусть функция u (x)

определена в некоторой окрестно-

сти O(x0 ) и дифференцируема в точке

x0 ; функция

y f (u) определена в

точке u0 :

u0 (x0 )

некоторой окрестности O(u0 )

и дифференцируема в

yx

lim

y

y

u

lim

y

lim

u

.

x

lim

x

u

x

x 0

x 0 u

x 0

x 0

Т.к. функция u (x) дифференцируема в точке x0 ,

а, следовательно, и не-

прерывна в точке x0 , то при x 0

также и u 0 . Следовательно,

yx

lim

y

lim

u

lim

y

lim

u

yu

ux .

Замечание.

x 0

u

x 0

x

u 0

u

x 0

x

Теорема остается справедливой и в случае,

если u будет об-

ращаться в нуль.

Пример 1.

Найти производную функции y (2x2 1)3 .

Решение.

2

2

2

2

2

5

3

y

3(2x

1)

(2x

1)

4x 48x

48x

12x .

1) 3(2x

ратная функция x f 1( y) будет дифференцируема в точке y

0

:

y

0

f (x ) и

производная обратной функции:

0

f 1( y0 )

1

.

f

(x0 )

Доказательство.

Рассмотрим точку x0

и значение функции y0 f (x0 ) . Рас-

смотрим точку x из окрестности точки x0

и y f (x) . x x0

x – прираще-

ние аргумента, тогда y будет меняться:

y y0 y .

f 1 ( y0 ) lim

x

y f (x) дифференцируема она

1

непрерывна x

f 1 ( y) непрерывна

lim

y 0

y

lim x 0

x 0

y

x

y 0

1

1

.

lim

y

x

f (x0 )

x

0