4. Свойства волновой функции. Квантование

Значение уравнении Шредннгера далеко не исчерпывается тем, что с его помощью можно найти вероятность нахождения частицы в различных точках пространства. Из этого уравнения и из условий, налагаемых на волновую функцию, непосредственно вытекают правила квантования энергии. Упомянутые условия состоят в том, что волновая функция в соответствии с ее физическим смыслом должна быть однозначной, конечной и непрерывной во всей области изменении переменных х, у и z. В уравнение Шредингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнение Шредингера, имеют решения, удовлетворяющие сформулированным выше условиям (т. е. однозначные, конечные и непрерывные), не при любых значениях параметра Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями параметра, а соответствующие им решения уравнения – собственными функциями задачи.

Отметим, что волновые функции должны быть всегда «нормированы» таким образом, чтобы

. (9)

Интегрирование производится по всей области изменения переменных х, у и z. Интеграл (9) представляет собой сумму вероятностей нахождения частицы во всех возможных элементах объема, т. е. вероятность обнаружить частицу в каком-либо месте пространства. Эта вероятность есть вероятность достоверного события и, следовательно, должна быть равна единице.

5. Частица в бесконечно глубокой одномерной потенциальной яме. Прохождение частиц через потенциальный барьер

Чтобы пояснить сказанное в предыдущем параграфе, рассмотрим конкретный пример, достаточно простой для того, чтобы уравнение Шредингера можно было легко решить.

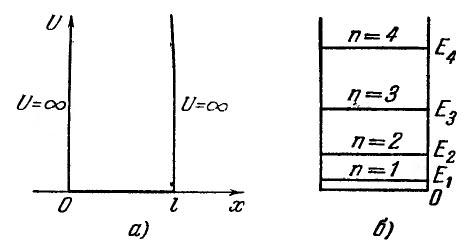
Исследуем поведение частицы в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U имеет в этом случае следующий вид (рис. 8, а): она равна нулю при 0 < х < l и обращается в бесконечность при х < 0 и х > l.

Поскольку функция зависит только от одной координатых, уравнение (4) будет иметь вид:

. (10)

За пределы потенциальной ямы частица попасть не может, поэтому вероятность обнаружить частицу, а следовательно и -функция за пределами ямы равна нулю. Далее, из условия непрерывности следует, чтодолжна быть равна нулю и на границах ямы:

и. (11)

Рис. 8.

Рис. 9.

Выражения (11) и определяют те условия, которым должны удовлетворять решения уравнения (10), имеющие физический смысл. В области, где не равна тождественно нулю, уравнение (10) принимает следующий вид:

. (12)

(U в этой области равна нулю). Введя обозначение получим уравнение, хорошо известное из теории колебаний:

. (12)

Решения такого уравнения, как известно, имеют вид:

.

Условиям (11) можно удовлетворить соответствующим выбором постоянных и. Из условия получаем, что. Далее, должно выполняться условие: ,что возможно лишь в случае, если

(n = 1, 2 3, …) (13)

(n = 0 отпадает, поскольку при этом получается тождественно равна нулю и частица нигде не находится).

Из (13) вытекает, что решения уравнения (12) будут иметь физический смысл не при всех значениях энергии Е, а лишь при значениях, удовлетворяющих соотношению:

(n = 1, 2 3, …).

Таким образом, не прибегая ни к каким дополнительным предположениям (как это пришлось сделать Бору), мы получили квантование энергии частицы и нашли собственные значения этой энергии:

(n = 1, 2 3, …). (14)

Схема энергетических уровней изображена на рис. 8, б. Произведем оценку расстояний между соседними уровнями для различных значений массы частицы т и ширины ямы l. Разность энергий двух соседних уровней равна . Если взятьт порядка массы молекулы, а l порядка 10 см (молекулы газа в сосуде), получается энергия 10^-32n эрг. Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что хотя квантование энергии в принципе будет иметь место, но на характере движения молекул сказываться не будет.

Аналогичный результат получается, если взять т порядка массы электрона при тех же размерах ямы (свободные электроны в металле). В этом случае будет иметь порядок 10^-28n эрг или 10^-16n эВ.

Однако совсем иной результат получается для электрона, если область, в пределах которой он движется, будет порядка атомных размеров (10^-8см). В этом случае будет иметь порядок 10^-10n эрг или 10²n эВ. Очевидно, что в этом случае дискретность энергетических уровней будет проявляться весьма заметным образом.

Собственными функциями, как следует из условия (13), будут

. (15)

Для нахождения коэффициента а воспользуемся условием нормировки (9), которое в данном случае запишется следующим образом:

.

На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение (равное, как известно, 1/2) на длину промежутка l. В результате получится: , откуда. Таким образом, собственные функции имеют вид:

(n = 1, 2, 3, …) (16)

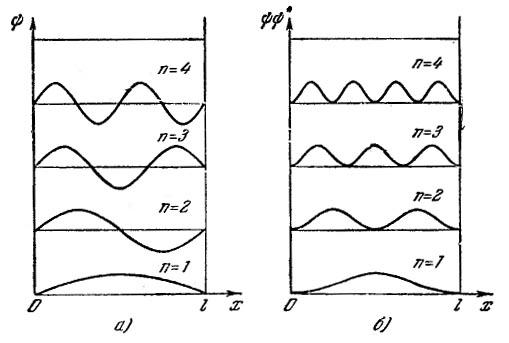
Графики функций (16) изображены на рис. 9, а. На рис. 9, б дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная . Как следует из графиков, частица в состоянии прип = 2 не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, очевидно, не совместимо с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.