Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

teoriticheskie_osnovy_elektrotekhniki_chast_1

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.02 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Следовательно, свободная составляющая напряжения на конденсаторе:

uc св = Aeρt = Ae−	t		−	t
	RC	= Ae		τ	.	(2.29)

Величина

τ = RC

называется постоянной времени. Она измеряется в секундах и характеризует скорость протекания переходного процесса. Считается, что переходный процесс заканчивается через t = (4 −5)τ .

Переходное напряжение на конденсаторе равно сумме принужденного и свободного напряжений:

		−			t
uc = uc пр + Ae		−
uc = uc пр + Ae				τ .		(2.30)
Принужденное напряжение						в цепи
(рисунок 2.12) равно ЭДС:
uc пр = E.
Tогда
	−		t
u = E +	−					(2.31)
u = E +	Ae	τ .				(2.31)
c

Постоянную интегрирования А найдем из начальных условий.

Пусть конденсатор был предварительно заряжен до напряжения U co . В мо-

мент включения (t = 0 )
uc =Uсо	(2.32)
Подставим (2.32) в (2.31) при t = 0 :

Uco = E + A,

откуда

A =Uco − E.

Следовательно, переходное напряжение на конденсаторе

− t

uc = E +(Uco − E)e τ . (2.33)

Если конденсатор не был заряжен до коммутации (U co = 0 ), то

				−	t

u	= E	1	−e		τ		(2.34)
u	= E	1	−e		τ	.	(2.34)
c

Ток в цепи с конденсатором:

	duc		E −Uco	e−	t
i = C		=			τ	. (2.35)
	dt
			R
			61

U i

E− UC 0

UC0			i


0			t

Рисунок

2 13

Графики изменения напряжения (2.33) и тока (2.35) приведены на рисунке

2.13.

Зарядный ток в начальный момент подключения конденсатора к источнику (при t = 0 ) увеличивается скачком, затем постепенно уменьшается. Конденсатор не оказывает сопротивления току в начальный момент времени, и ток ограничен только активным сопротивлением цепи R.

Напряжение на конденсаторе согласно второму закону коммутации не может измениться скачком. Оно увеличивается постепенно. Переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается через t = (4 −5)τ .

2.11 ПРОЦЕСС РАЗРЯДА КОНДЕНСАТОРА

Предполагается,

что

конденсатор

был заряжен до на-

пряжения U co . При

UC0

замыкании

цепи

C–

(рисунок 2.14) начи-

нается

разряд кон-

денсатора.

Рисунок 2.14

Замыкание

цепи

равносильно

приня-

тию

в уравнении

(2.33) ЭДС, равной нулю.

Подставим в (2.33) и (2.35) E = 0 :

−

;

(2.36)

U co

e−

i = −

τ .

(2.37)

Знак минус показывает, что ток направлен противоположно по отношению к тому току, который был при заряде конденсатора.

U
	UC
0	t
	i

Графики изменения напряжения и тока приведены на рисунке 2.15. Ток в цепи в начальный момент времени (при t = 0 ) изменяется скачком, затем плавно уменьшается. Напряжение скачком не изменяется.

Так же как и в предыдущем случае, переходный процесс можно считать законченным через t = (4 −5)τ . К этому времени конденсатор разрядится на 98,2–99,3%.

закону коммутации не может прерваться мгновенно. В начальный момент времени ток i остается таким же, каким он был перед коммутацией. Но теперь он замыкается по новому пути – через резистор R1 ( в замкнутом контуре R1, L, R). При этом ток через R1, который был до коммутации, изменился скачком. Он принял противоположное направление в соответствии с направлением тока i через индуктивность.

Уравнение напряжений для цепи (рисунок 2.16) после коммутации:

(R +R ) i +L	di	= 0	(2.39)

1	dt

или в алгебраической форме:

(R1 +R ) i +L ρ i = 0.

Так как в цепи нет ЭДС, то уравнение (2.39) – однородное. Имеется только свободная составляющая тока.

Характеристическое уравнение:

(R1 +R )+L ρ = 0.

Корень уравнения:

2.12 РАЗМЫКАНИЕ ЦЕПИ С

ρ = −

R1 +R

ИНДУКТИВНОСТЬЮ

При размыкании электрической це-

Решением

однородного

уравнения

является показательная функция:

пи, обладающей индуктивностью, между

контактами выключателя возникает элек-

i = Ae ρt = Ae −

трическая дуга (искра), а на отдельных уча-

, . (2.40)

стках цепи могут появляться напряжения,

где

τ =

во много раз превышающие установившие-

ся значения. Такие напряжения называются

перенапряжениями. Они могут быть на-

Постоянную интегрирования А на-

столько большими, что вызовут пробой

ходим из начальных условий. В начальный

изоляции, повреждение измерительной ап-

момент времени (при

t = 0 ) ток через ин-

паратуры и т.п.

дуктивность

сохраняет свое

значение

Рассмотрим

процесс

отключения

(2.38):

цепи с индуктивностью от источника по-

i = I0

стоянной ЭДС (рисунок 2.16).

В ветви с индуктивностью до раз-

Подставим это значение в уравнение (2.40)

мыкания цепи был установившийся ток

при t = 0 :

i = I0 =

(2.38)

= A.

При

Тогда переходный ток через индуктивность

размыкании

согласно формуле (2.40):

цепи

ток че-

−

рез индуктив-

τ .

i =

= I 0e

(2.41)

ность

соглас-

но

первому

При изменении тока возникает ЭДС

самоиндукции:

Рисунок 2.16

= −L

ветвь с резистором R1 (что соответствует

R1 = ∞), то согласно формуле (2.43)

учетом

тока

(2.41)

значения

τ (2.40):

= −L

−

R + R

− R1 +R

или

Рисунок 2.19

Рисунок 2.20

= E (R + R)e− τ .

(2.42)

eL (0) → ∞

Ток в цепи после коммутации (после

и перенапряжение, а следовательно, и на-

размыкания) поддерживается за счет ЭДС

пряжение

на выключателе

должно быть

самоиндукции:

равно бесконечности. Но физически этого

i =

не может быть. В действительности под

R1 +R .

действием

возрастающего

напряжения

Значение ЭДС самоиндукции в пер-

произойдет пробой промежутка между кон-

вый момент после размыкания цепи (при

тактами выключателя, и в цепь будет

t = 0 ):

включено

сопротивление

электрической

(0) =

R1 + R E.

(2.43)

дуги.

практике вместо

резистора R1

На

Оно больше ЭДС источника E во столько

(рисунок 2.16) включают выпрямительный

раз, во сколько увеличилось сопротивление

диод VD (рисунок 2.18). При размыкании

цепи, то есть в

(R +R ) R раз. Это явление

цепи ток i через индуктивность не преры-

вается, так как замыкается через диод в

называется перенапряжением.

E i

контуре L, R, VD.

2.13 НЕСИНУСОИДАЛЬНЫЕ

ТОКИ И ПРИЧИНЫ ИХ

ВОЗНИКНОВЕНИЯ

Синусоидальные

и косинусоидаль-

ные функции в общем случае называются

Рисунок 2.17

гармоническими функциями или просто

гармониками.

Графики изменения тока и ЭДС са-

Гармоническая

(синусоидальная)

моиндукции представлены на рисунке 2.17.

форма токов и напряжений в электротехни-

ЭДС самоиндукции в начальный момент

ке является основной. Она наиболее выгод-

времени делает скачок. Ток же в индуктив-

на в технико–экономическом отношении по

ности согласно первому закону коммута-

сравнению с негармонической формой. Од-

ции не может изменяться скачком. Он из-

нако тенденция развития электротехники

меняется

по-

такова, что заметное распространение по-

степенно

от

лучают и цепи с негармоническими токами

начального

и напряжениями. Это цепи различных элек-

значения I0.

тромагнитных и электронных устройств.

Если

Несинусоидальность

появляется

цепь (рисунок

тех цепях, в состав которых входят нели-

2.16) не будет

нейные элементы.

содержать

Рисунок 2.18

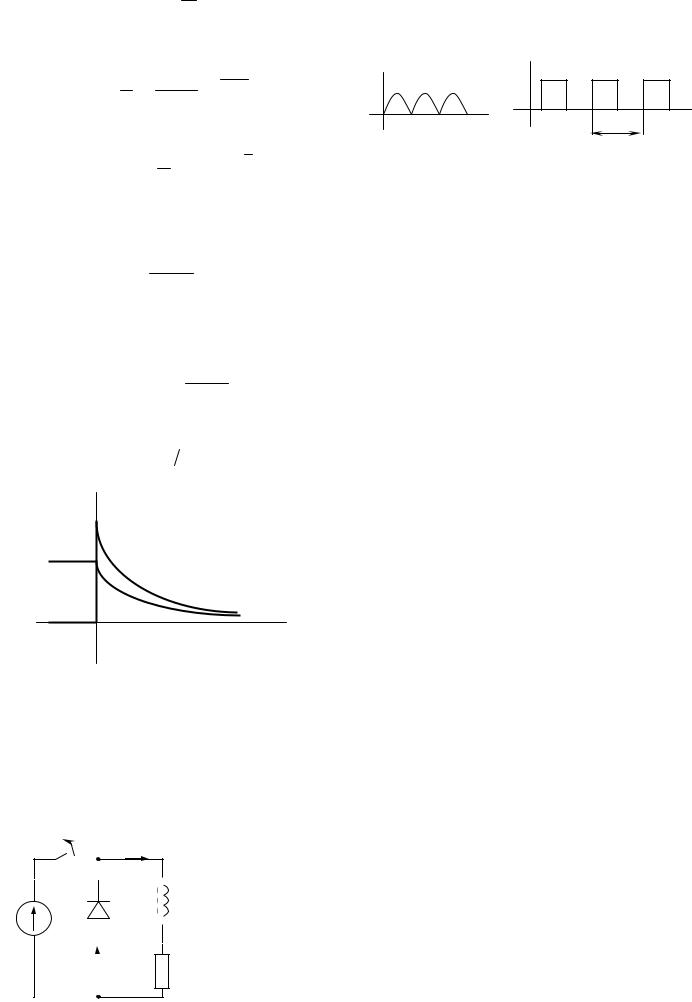
Наибольшее распространение негармонические токи и напряжения получили в электронике. Электронные устройства (силовые преобразователи электроэнергии и информационные устройства) по принципу своего действия создают негармонические токи и напряжения.

В качестве примера на рисунке 2.19 показана несинусоидальная форма выпрямленного напряжения однофазного выпрямителя, преобразующего синусоидальный ток в постоянный, а на рисунке 2.20 – несинусоидальная форма напряжения, применяемая в информационных электронных устройствах.

2.14 РАЗЛОЖЕНИЕ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ В РЯД ФУРЬЕ

Для расчета негармонических токов и напряжений нужно знать способы их математического описания.

Периодическая несинусоидальная функция u(t) может быть представлена в

виде гармонического ряда Фурье: u(t)=U 0 +U1m sin(ωt +ϕ1)+

+U2m sin(2ωt +ϕ2 )+

+... +Uκm sin(κωt +ϕκ )+... = (2.44)

∞

U0 + ∑Uκm sin(κωt +ϕκ ),

κ=1

где к = 1,2,3…,

U0 – постоянная составляющая; U1m ,U2m ...Uκm – амплитуды пер-

вой, второй, к –ой гармоники; ϕ1,ϕ2 ...ϕκ - начальные фазы.

Синус суммы двух углов в уравнении (2.44) преобразуется по известной тригонометрической формуле:

Uκm sin(κωt +ϕκ )=Uκm sinκωt cosϕκ +

+Uκm cosκωt sinϕκ .
Обозначим:
Aκm =Uκm cosϕκ ,					(2.45)
B	=U	κm	sinϕ	κ.
κm		κm		κ.

С учетом этого получим преобразованную

формулу (2.44):

u(t)=U0 + ∑∞ (Aκm sinκωt + Bκm cosκωt),

κ=1

(2.46)

где коэффициенты ряда Фурье находят по формулам:

Aκm = 2 ∫u(t)sinκωt dt, (2.47) T 0

Bκm = 2 ∫u(t)cosκωt dt. (2.48) T 0

Угловая частота несинусоидальной функции:

ω =2πf =	2π	,	(2.49)
	T

где Т – период несинусоидальной функции.

Частота к – ой гармоники равна κω . При к=1 будет частота первой гармоники, при к=2 – частота второй гармоники и т.д.

Вычислив коэффициенты (2.47) и (2.48), можно перейти к формуле (2.44), в которой на основании соотношений (2.45):

U	κm	= A2		+B2		,	(2.50)
		κm			κm
ϕκ		= arctg	Bκm		.		(2.51)

			Aκm

Постоянная составляющая ряда является средним значением функции за период:

U 0 =	1	T u(t)dt.	(2.52)
U 0 =	T	T u(t)dt.	(2.52)
	T	∫
		0

Таким образом, несинусоидальная периодическая функция может быть представлена в виде суммы гармоник.

2.15 ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯНЕСИНУСОИДАЛЬН ЫХ ТОКОВ

Действующее значение несинусоидального тока определяется на основании известной из теории синусоидального тока формулы:

	1	T
I =	1	∫i2dt .
	T	0
		0

Подставим в эту формулу выражение несинусоидальной функции i в виде ряда Фуре и проведем необходимые математические преобразования. В результате получим следующую формулу для действующего значения несинусоидального тока:

	I =	I02 + I12 +... + Iκ2 +...,			(2.53)
где	I0 – постоянная составляющая гар-
монического ряда;
	Iκ	– действующее значение к – ой
гармоники тока:
		Iκ =	Iκm	,
		Iκ =	2	,
			2
	Iκm	– амплитуда к –ой гармоники

тока.

Подобным образом определяется действующее значение несинусоидального напряжения:

U = U 02 +U12 +... +Uκ2 +...,			(2.54)
где
Uκ =	Uκm	.
Uκ =	2	.
	2

Средняя за период (активная) мощность цепи несинусоидального тока равна сумме средних мощностей гармоник:

P =U0I0 +U1I1 cosϕ1	+...	(2.55)
... +Uκ Iκ cosϕκ +...		(2.55)
... +Uκ Iκ cosϕκ +...

Существует понятие эквивалентной синусоиды. Оно возникло в связи с тем, что иногда в приближенных расчетах при отсутствии постоянных составляющих несинусоидальный ток заменяют эквивалентным синусоидальным током. При этом действующее значение эквивалентного синусоидального тока принимают равным действующему значению заменяемого несинусоидального тока:

I экв = I , U экв =U ,

где I и U соответствуют значениям (2.53) и (2.54) при I0 = 0, U0 = 0.

Угол сдвига фаз между эквивалентными синусоидами тока и напряжения определяется на основании формулы:

где P – сумма активных мощностей гармоник (2.55);

UI = S – полная мощность.

2.16 РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ С НЕСИНУСОИДАЛЬНОЙ ЭДС

Для расчета линейной электрической цепи с несинусоидальной ЭДС применяют метод наложения. Он заключается в том, что после разложения заданной ЭДС в ряд Фурье задачу решают для каждой гармоники в отдельности по принципу независимости действия гармоник в линейных электрических цепях. Считают, что каждая гармоника напряжения создает только свою гармонику тока и не имеет никакого отношения к другим гармоникам. Задачи для отдельных гармоник решают однотипно. Затем найденные мгновенные значения отдельных гармоник токов складывают.

Например, требуется найти ток в цепи (рисунок 2.21) при заданных значениях параметров R, L, C. Напряжение задано в виде несинусоидальной функции

u(t)=U m1 sin(ωt +ϕu1 )+U m3 sin(3ωt +ϕu3 ).

Схема данной цепи (рисунок 2.21) разбивается на две подсхемы. В первой из

i			i1			i3
	R		R				R
U(t)	L	U1	XL1	+		U3	XL3
				+
	C		XC1				XC3
Рисунок 2.21		Рисунок 2.22			Рисунок 2.23

них (рисунок 2.22) действует первая гармоника заданного напряжения

u1 =U m1 sin(ωt +ϕu1 ),

во второй (рисунок 2.23) – третья гармоника:

u3 =U m3 sin(3ωt +ϕu3 ),

Сопротивление для к – ой гармоники тока рассчитывают для частоты κω :

cosϕэ =	P	,	(2.56)	Z κ = R 2 +X κ2 , ϕκ	= arctg	X κ	,
	UI

						R
			65

=U1e jϕu1 .

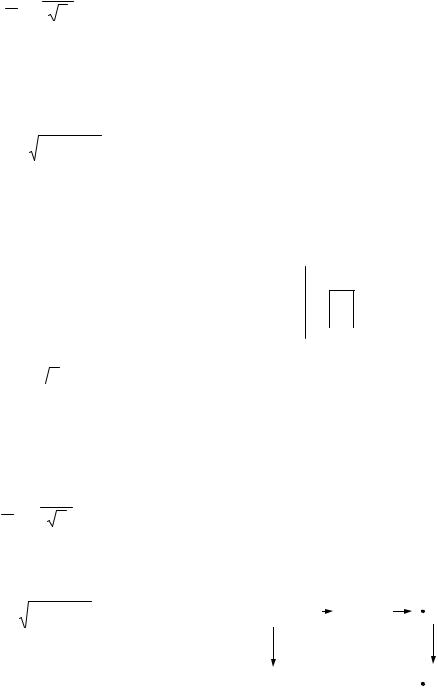
где	Xκ = X Lκ − XCκ ,			i = i1 +i3	= I m sin(ωt +ϕu −ϕ1)+
					1	1
	X L κ =κωL, X Cκ =	1	.	+ I m3 sin(3ωt +ϕu3		−ϕ3 ).
	X L κ =κωL, X Cκ =		.	+ I m3 sin(3ωt +ϕu3		−ϕ3 ).
		κωC

Первая гармоника тока i1 определяется следующим образом.

Записываем первую гармонику заданного напряжения в комплексной форме:

U1 = U m21 e jϕu1

Комплексное сопротивление для первой гармоники тока находим для частоты ω :

= Z e jϕ1 , ϕ

= arctg

Z1 = R 2 +X12 ,

x1 =ωL −

ωC

Комплексное значение первой гар-

моники тока:

1 =

U e jϕu1

= I e

j (ϕu −ϕ1 )

1 .

Z e jϕ1

От комплексного значения I1 переходим к

мгновенному значению первой гармоники тока:

i1 = I m1 sin(ωt +ϕu1 −ϕ1),

где I m1 = 2I1.

Третья гармоника тока i3 определя-

ется как и первая гармоника, но для частоты 3ω .

Напряжение

U 3

U m

jϕu

=U3e

jϕu

3 .

Сопротивление:

Z 3 = Z3e

jϕ

= arctg

Z 3 = R 2 +X 32 ,

= 3ωL −

3ωC

Комплексное значение третьей гар-

моники тока:

I 3 =

3 =

e jϕu3

= I

j (ϕu

−ϕ

)

Z 3

Z3e jϕ 3

Мгновенное значение третьей гармоники тока:

i3 = I m3 sin(3ωt +ϕu3 −ϕ3 ),
Ток в цепи:	66
	66

2.17НЕПЕРИОДИЧЕСКИЕ ТОКИ

ИНАПРЯЖЕНИЯ

До сих пор мы рассматривали периодические функции (синусоидальные и несинусоидальные токи и напряжения). Периодическими называют функции, которые удовлетворяют условию периодичности. К ним относятся гармонические функции и периодические последовательности импульсов различной формы. Предполагается, что они не имеют ни начала, ни конца во времени.

Если функции не отвечают условию периодичности, то они называются непериодическими. Обычно они ограничены во времени. К ним относятся одиночные импульсы или группы импульсов различной

формы, или отрез-

Uки периодических функций. В качестве примера непе-

			риодической
0	t		риодической
Рисунок 2.24		функции на рисун-
Рисунок 2.24		ке	2.24. представ-
		лен	одиночный

прямоугольный импульс напряжения.

Для математического описания непериодических функций применяется преобразование Фурье (см. главу 4).

2.18 УРАВНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА

Четырехполюсник – это устройство

между источником и приемником					электро-
		I1	I2		энергии
		I1	I2		энергии
					(рисунок
					2.25).
	U1		U2	Zн

					Имеет


				две пары
				две пары
					выводов
	Рисунок 2.25				выводов
	Рисунок 2.25				(четыре

полюса). Входные выводы – со стороны источника, выходные выводы – со стороны нагрузки.

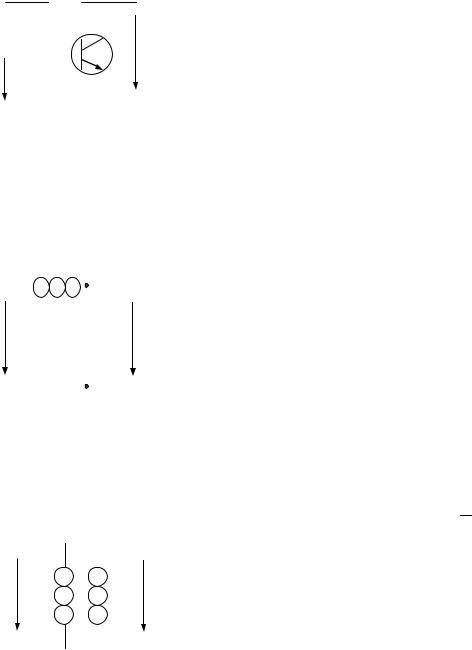
U1, I1 – входное напряжение и вход-

образной, П–образной или Г–образной схе-

ной ток;

ме замещения.

U2 , I2 –

выходное

напряжение и

В Т–образной схеме (рисунок 2.29)

три резистора соединены звездой. Для этой

выходной ток.

схемы может быть составлена следующая

Положительные

направления

на-

пряжений и токов показаны на рисунке

система уравнений:

2.25.

I 1

= I 2 + I 3 ,

Теория

четырехполюсника

применяется,

U 1

= Z 1 I 1 + Z 2 I 2

(2.57)

+U 2 ,

когда нужно знать токи и напряжения на

Z 3 I 3 = Z 2 I 2 +

2 .

выводах,

а не внутри самого

четырехпо-

Систему уравнений (2.57) преобра-

люсника.

зуют так, чтобы получить уравнения вида:

четырехполюсникам

относятся,

например,

электрон-

= AU 2 + BI 2 ,

(2.58)

I1 = CU 2 + DI

ный усилитель (ри-

сунок 2.26), электри-

где

ческий фильтр (ри-

A =1+

, B = Z1 + Z 2 +

сунок

2.27),

транс-

форматор

(рисунок

(2.59)

C = 1

2.28)

другие

уст-

, D =1+ Z 2 .

ройства,

которые

Z 3

Рисунок 2.26

включены в электри-

А, В, С, D – комплексные коэффици-

ческую цепь как пе-

енты. Их определяют опытным или расчет-

редаточное звено с двумя парами выводов

ным путем. Они связаны соотношением

между источником и приемником электро-

АD − ВС =1.

(2.60)

энергии. Простейшим четырехполюсником

По коэффициентам А, В, С, D можно

является двухпроводная линия,

соединяю-

определить

Z ,

щая источник и приемник электроэнергии.

Z 1 =

A −1

Z 2

D −1

Z 3

(2.61)

Четырехпо-

люсники

могут

быть

Если

А = D ,

то

четырехполюсник

линейные,

нелиней-

симметричен. В нем

ные, пассивные, ак-

тивные.

активным

Z 1 = Z 2 .

относятся

четырехпо-

Для П–образной схемы (рисунок

Рисунок 2.27

люсники, которые со-

2.30) подобным образом получают те же

держат

внутри

себя

уравнения, что и для Т–образной схемы, но

источники

коэффициенты будут иметь другие значе-

электроэнергии. Если внутри четырехпо-

ния:

= AU

+ BI

люсника нет источников, то его называют

пассивным.

I1 = CU

2 + DI 2 ,

Активный

четырехполюсник

пока-

где

зан

на

рисунке

2.26,

пассивные – на ри-

A =1+

, B = Z 4 ,

U2 сунках 2.27 и 2.28.

Z 6

(2.62)

Любой

пас-

Z 4 + Z 5 + Z 6

Z 4

C =

, D

=1+

сивный

Z 5 Z 6

Z 5

люсник,

сопротивле-

Рисунок 2.28

ния

которого

янны,

можно

путем

преобразования

схемы

привести

Т–67

Комплексные коэффициенты А, В, С, D здесь также связаны между собой соотношением (2.60).

Zн

Z2 Рисунок

2.30

Zн

Если

A = D ,

то

четырехполюс-

ник симметричен и

Рисунок 2.29

Z 5 = Z 6.

По коэффициентам А, В, С, D можно

определить сопротивления:

Z 4

= B, Z 5 =

, Z 6

(2.63)

D −1

А −1

Κu (ω), Κi (ω) – амплитудно– частотные характеристики;

ϕu (ω), ϕi (ω) – фазочастотные ха-

рактеристики.

Эти характеристики применяются при анализе работы электронных и автоматических устройств.

2.20 ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ

Электрический фильтр – это четырехполюсник, назначение которого состоит в том, чтобы пропускать токи одних частот

изадерживать токи других частот.

Взависимости от пропускаемого спектра частот различают:

–фильтры нижних частот (низкочастотные) – пропускают токи нижних частот

(рисунок 2.31);

2.19 ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЧЕТЫРЕХПОЛЮСНИКА

Отношение выходной величины ко входной называют передаточной функцией (или коэффициентом передачи) четырехполюсника.

Передаточная функция по напряже-

нию:

+B I 2

(2.64)

Z нI 2

Z н

AZ нI 2 +B I 2

AZ н +B

Рисунок 2.31

– фильтры верхних частот (высокочастотные) – пропускают токи верхних частот (рисунок 2.32);

Передаточная функция по току:

I 2

+ DI 2

(2.65)

I 2

СZ н I 2 + DI 2

СZ н + D

Κu и Κi – комплексные величины.

Впоказательной форме они имеют вид:

Κu = Κue jϕu , Κi = Κie jϕi ,

где Κu , Κi – модули;

ϕu , ϕi – фазы передаточных функ-

ций.

Зависимости амплитуд и фаз от частоты называются частотными характеристиками: 68

Рисунок 2.32

Рисунок 2.33

Рисунок 2.34

– полосовые фильтры – без большого ослабления пропускают токи узкой полосы частот (рисунок

2.33); заграж-

дающие фильтры – сильно ослабляют (не пропускают) токи определенной поло-

сы частот (рисунок 2.34).

ТРЕХФАЗНЫЕ ЦЕПИ

Действие фильтров объясняется тем,

Программа работы. Измерить и вы-

что на нижних частотах индуктивные со-

числить

линейные и

фазные величины и

противления малы, а емкостные – велики;

на верхних частотах наоборот – индуктив-

ные сопротивления велики, а емкостные –

малы. Поэтому, например, в фильтре ниж-

них частот токи нижних частот без большо-

го ослабления проходят через индуктив-

ность в сопротивление нагрузки Z н, лишь

в малой части ответвляясь в конденсатор

Рисунок 2.38

0	f0	f	0	f0	f
Рисунок 2.35			Рисунок 2.36

(рисунок 2.31).

В полосовых и заграждающих фильтрах используются резонансы напряжений и токов для отдельных гармоник. Например, чтобы пропустить только одну ν –ю гармонику тока и не пропускать все другие гармоники, применяют полосовой фильтр, в котором участки LC (рисунок 2.33) настраивают на резонанс для ν –ой гармоники. Настройка проводится, например, путем изменения емкости C, чтобы на резонансной частоте получить максимум тока на участке с последовательно соединенными L и C (резонанс напряжений) и минимум тока на участке с параллельно соединенными L и С (резонанс токов).

Резонансные характеристики для участков с последовательным и параллельным соединением L и C приведены на ри-

сунках 2.35 и 2.36.

соотношения между ними при симметричной и несимметричной нагрузке фаз. Сделать выводы относительно роли нулевого провода. По результатам измерений заполнить таблицы 2.1. и 2.2. для соединения фаз звездой (рисунок 2.37) и треугольником (рисунок 2.38). Построить векторные диаграммы на комплексной плоскости.

Таблица 2.1.

U A U B UC U AB U BC UCA I A I B IC I N P

Таблица 2.2.

U AB U BC UCA I AB I BC ICA I A I B IC P

2.22 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

•Задача 2.1 Вычислить линейные и фазные токи и начертить векторную диаграмму для трехфазной цепи (рисунок

2.39).

2.21 ЛАБОРАТОРНАЯ РАБОТА 2.1					Параметры цепи:
					R1 = 22 Ом, R2 =19 Ом, ХС =11 Ом,
	V			V	R3 =19 Ом, ХL =11 Ом.
					Система линейных напряжений
A					Система линейных напряжений
A					симметрична:
B			A		симметрична:
					U л =U AB =U BC =UCA = 220 B.



C					Решение.
					69


N	Рисунок
N

		2.37

Комплексные сопротивления приемников электроэнергии:

Z AB = R1 = 22 Ом,

Z BC = R2 − jX C =19 − j11 Ом, Z CA = R3 + jX L =19 + j11 Ом.

Запишем комплексные значения линейных напряжений. Так как начальная фаза не задана то для напряжения U AB примем её равной нулю:

I AB

I A

I BC

I B

ICA R3

X L

Рисунок 2.39

U AB =U ABe j0 =U л = 220 В.

Тогда

= 220(cos1200 − j sin1200 )=

BС =U лe− j1200

−

− j

= −110 − j190

В.

= 220

CA =U лe− j2400 =U лe j1200 =

= 220(cos1200 + j sin1200 )=

−

+ j

= −110 + j190 В.

= 220

Фазные токи:

I AB =

220

=10 A,

Z AB

BC =

−110 − j190

= − j10

Z BC

19 − j11

I CA =

−110 + j190

= j10 A.

Z CA

19 + j11

Линейные токи:

I A = I AB − I CA =10 − j10 A,

I B = I BC − I AB = − j10 −10 A,

I C = I CA − I BC = j10 −(− j10)= j20 A.

Сумма линейных токов в трехпроводной трехфазной цепи равна нулю:

I A + I B + I C = I AB −I CA + I BC −

−I AB + I CA −I BC = 0. 70

Проверим это:

I A + I B + I C = (10 − j10)+ +(− j10 −10)+ j20 = 0.

Векторная диаграмма токов и напряжений показана на рисунке 2.40. Масштаб:

UCA	ICA
UCA
	UAB	IAB
				+
				+
IB			-ICA

UBC IBC

-IАВ

-j

Рисунок 2.40

mu =20 ммB , mi = 0,5 ммA .

•Задача 2.2 Определить ток, актив-

i				ную мощность и
				полную	мощ-
				полную	мощ-
				ность цепи (рису-
	R
	R	L	C
U			C	нок 2.41).
U				нок 2.41).
				Параметры
Рисунок 2.41				цепи:
Рисунок 2.41				R =10 Ом,

L = 0,05 Гн, С = 22,5 мкФ,

u =180sinωt +60sin 3ωt +40sin(5ωt +180 )B.

Частота первой гармоники f = 50 Гц . Решение.

Комплексное сопротивление для первой гармоники тока:

X L1 =ωL = 2πfL = 2 3,14 50 0,05 =15,7 Ом.

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019104.96 Кб2Tehnologiya-transportnyh-processov.doc
#
21.11.2019107.52 Кб2Teil Passau aus Кравченко.doc
#
10.09.2019163.33 Кб2Tema16(konsolid).doc
#
14.02.20152.1 Mб74Teoria2.doc
#
14.02.2015989.2 Кб23teoriticheskie_osnovy_elektrotekhniki_chast2.pdf
#
14.02.20151.02 Mб22teoriticheskie_osnovy_elektrotekhniki_chast_1.pdf
#
14.02.20152.94 Mб11teoriya-Avtokad-2013.pdf
#
12.03.20164.75 Mб195terehova_vupap.pdf
#
14.02.2015275.46 Кб174Termodinamika_metodichka.doc
#
11.11.2019926.72 Кб88test фарм.doc
#
14.02.2015131.58 Кб151Testy_k_zachet2012.doc