teoriticheskie_osnovy_elektrotekhniki_chast_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

i = I m sin(ωt +ϕu +900 ) ,

где Im =ω C Ucm =

Величина X C

называется

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.02 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

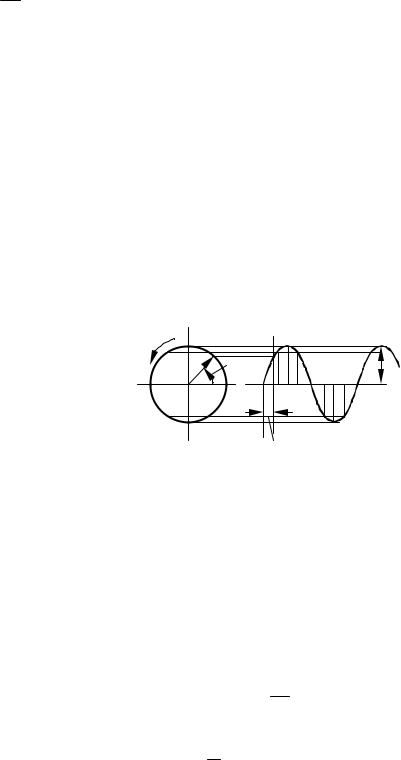
На рисунке 1.49 показано электро-					– Основные потребители электро-
				энергии – электрические двигатели пере-
магнитное устройство с двумя обмотками				менного тока также являются более пред-
(трансформатор), принцип действия кото-				почтительными, чем двигатели постоянно-
рого основан на использовании явления				го тока.
взаимной индукции. Его электрическая					– Постоянный ток проще получать
схема приведена на рисунке 1.50.				путем преобразования (выпрямления) пе-
ЭДС взаимной индукции наводится				ременного тока, чем с помощью генерато-
во вторичной обмотке при изменении тока				ров постоянного тока.
в первичной обмотке:					Синусоидальный ток является част-
	e = −M di1 ,		(1.49)	ным случаем переменного тока.
	2	dt			Переменным называют ток, величи-
где M – взаимная индуктивность обмо-				на и направление которого периодически
ток;				изменяются.
i1 – ток в первичной обмотке;					Главное		преимущество	синусои-
e – ЭДС взаимной индукции, наве-				дального тока перед переменным током
2				любой другой формы состоит в том, что
денная во вторичной обмотке.				потери мощности в цепи при синусоидаль-
Если	имеется взаимная индукция,
				ном токе оказываются наименьшими.
то говорят,	что обмотки	индуктивно или			1.26 ИЗОБРАЖЕНИЕ
магнитно связаны. Связь осуществляется
					СИНУСОИДАЛЬНЫХ
посредством магнитного потока Ф. В уст-
				ФУНКЦИЙ ВРАЩАЮЩИМИСЯ
ройстве на рисунке 1.49 магнитный поток
Ф, созданный током i1 ,		пронизывает обе			ВЕКТОРАМИ
					Любая		синусоидальная	функция
обмотки и называется магнитным потоком
				может	быть	представлена на		плоскости
взаимной индукции.				вращающимся вектором.
Взаимная индуктивность, как и ин-
дуктивность, измеряется в генри (Гн).				ω	+		i

В отличие от собственной индук-					Im
						ϕi
тивности L взаимная индуктивность M обо-								Im
значает не	какой–либо	самостоятельный		+j			0	ωt
элемент электрической цепи, а лишь маг-

нитную связь между индуктивными эле-							ϕi
ментами.	1.25 ПРИЧИНЫ
							Рисунок 1.51
ПРИМЕНЕНИЯ

СИНУСОИДАЛЬНОГО ТОКА					На рисунке 1.51 показан вращаю-
Синусоидальный ток получил рас-
				щийся вектор тока. Положительное направ-
пространение после того, как М.О. Доливо				ление вращения принято против хода часо-
– Добровольский изобрел систему трехфаз-				вой стрелки. Вектор вращается с постоян-
ного тока. В качестве формы тока он реко-				ной угловой скоростью ω = const. За вре-
мендовал синусоиду.				мя, равное периоду T, вектор поворачивает-
Синусоидальный ток имеет сле-
				ся на 2π рад. Следовательно, его угловая
дующие преимущества перед постоянным				скорость:
током.							ω = 2π =2πf ,	(1.50)
– Для производства электроэнергии
используются генераторы переменного то-							T
				где	T – период (с);
ка, которые	в экономическом		отношении
выгоднее генераторов постоянного тока.					1
					f =T	– частота тока (Гц).
			21

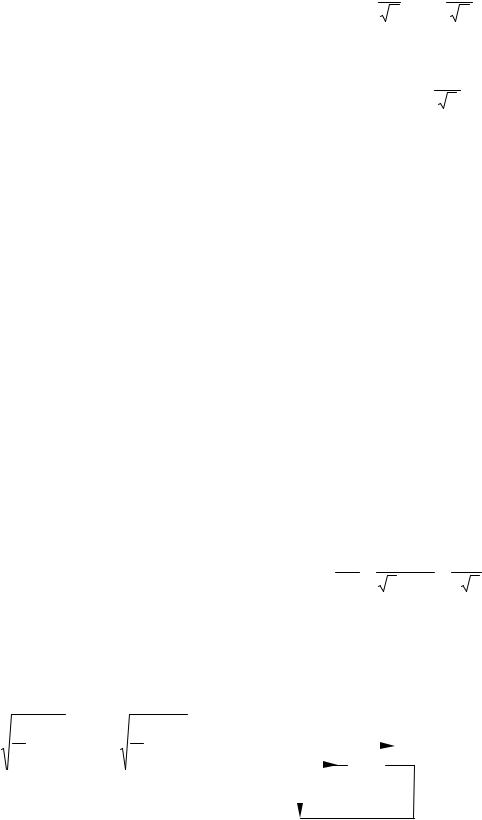
Угловую скорость вектора ω назы-

образования, то можно получить следую-

вают угловой частотой.

щие соотношения

между

действующими

В начальный момент времени (t =0)

значениями и амплитудами:

вектор расположен под углом ϕi

к положи-

I =

I m ,

U =U m

(1.53)

тельному направлению оси абсцисс. Угол

ϕi , определяющий значение тока в началь-

Такое же соотношение можно вы-

ный момент времени, называют начальным

вести и для ЭДС:

фазовым углом или просто начальной фа-

E =

(1.54)

зой.

Индексами i, e, u

будем обозначать

1.28 СРЕДНИЕ ЗНАЧЕНИЯ

начальные фазы тока (ϕi ), ЭДС (ϕe ), на-

ТОКА И НАПРЯЖЕНИЯ

пряжения (ϕu ).

Под средним значением синусои-

Проекции вращающегося вектора на

дальной функции понимают среднее её

ось ординат выражают мгновенные значе-

значение за половину периода.

ния синусоидального тока:

Для тока

i = I m sinωt = I m sinα

i = I m sin(ωt +ϕi ),

(1.51)

где

i – мгновенное значение тока;

среднее значение:

I m

– амплитуда тока (модуль вра-

I ср =

∫I m sinαdα =

I m .

(1.55)

щающегося вектора);

ϕi

– начальная фаза.

Такие же соотношения существуют

В нашей стране и большинстве дру-

и для средних значений синусоидальных

гих стран частота промышленного тока

напряжений и ЭДС:

равна 50 Гц. В США принята частота 60 Гц.

1.27 ДЕЙСТВУЮЩИЕ

U ср ==

U m ,

Eср ==

(1.56)

ЗНАЧЕНИЯ ТОКА И

Отношение действующего значения

НАПРЯЖЕНИЯ

к среднему значению называют коэффици-

Номинальные величины токов и на-

ентом формы кривой. Для синусоиды ко-

пряжений

электротехнических

устройств

эффициент формы имеет следующее значе-

выражаются не амплитудами, а действую-

ние:

щими значениями. Все расчеты также про-

I m π

2 ≈1,11 . (1.57)

водятся с действующими значениями.

Кф = I ср

2 2I m

= 2

Электроизмерительные

приборы

электро-

магнитной и электродинамической систем

1.29 ТОК И НАПРЯЖЕНИЕ В

показывают действующие значения.

ЦЕПИ С АКТИВНЫМ

Действующее значение – это сред-

нее квадратичное значение за период тока,

СОПРОТИВЛЕНИЕМ

напряжения, ЭДС:

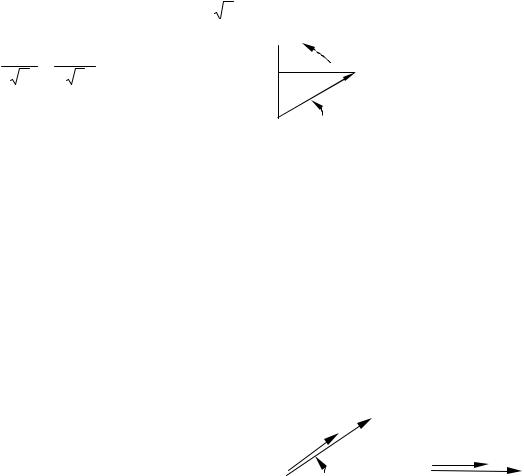
На рисунке 1.52 представлена элек-

1 T

трическая цепь сину-

соидального

тока с

I =

∫i

dt , U =

∫u

(1.52)

активным сопротив-

лением

Положи-

где

I, U –

действующие значения тока,

тельные направления

напряжения;

тока

напряжения

i, u – мгновенные значения тока, на-

показаны стрелками.

пряжения.

Рисунок 1.52

Мгновенное

Если в (1.52) подставить формулы

значение тока:

мгновенных значений тока и напряжения

i = I m sin(ωt +ϕi ) .

вида (1.51) и выполнить необходимые пре-

Мгновенное				значение		напряжения
на резисторе:
uR = R i = RI m sin(ωt +ϕi ) .							(1.58)
Произведение			R I m является			амплитудой
напряжения:
		U Rm = R I m .
Разделим амплитуду напряжения на							2 и
получим действующее значение:
U R =	U Rm	=	R I m		= RI ,	(1.59)
	2			2

где U R и I – действующие значения на-
пряжения и тока.							0
Из (1.58) следует, что напряжение
на резисторе имеет ту же начальную фа-
зу, что и ток:
			ϕu =ϕi .				(1.60)

В таком случае говорят, что напряжение и ток совпадают по фазе.

1.30 ВЕКТОРНАЯ ДИАГРАММА

Синусоидальные величины можно графически изображать или синусоидами, или вращающимися векторами. В дальнейшем будем пользоваться только векторными диаграммами. Их преимущество заключается в том, что графические операции с векторами (графическое изображение векторов, их сложение или вычитание) гораздо проще и быстрее, чем те же действия при графическом изображении синусоид.

На векторной диаграмме изображают векторы в начальный момент времени. Вращение векторов происходит с одной и той же угловой скоростью, и, следовательно, их взаимное расположение остается неизменным.

Начало отсчета времени можно выбрать произвольно, то есть один из векторов можно направить произвольно. Тогда остальные векторы будут располагаться относительно первого вектора.

Длина вектора в масштабе представляет амплитуду синусоиды. Угол, образованный вектором с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе. Скорость вращения вектора равна угловой час-

тоте. Мгновенные значения синусоидальной величины (тока или напряжения) выражаются проекциями вращающегося вектора на ось ординат.

Векторная диаграмма строится следующим образом. Ток i = I m sin(ωt +ϕi )

изображается в начальный момент времени (t = 0) вектором,

ωрасположенным под

i	Im	углом ϕi	к положи-
	ϕi	тельному	направле-
	ϕi	нию оси абсцисс
		(рисунок	1.53).
	Рисунок 1.53	(рисунок	1.53).
	Рисунок 1.53	Длина	вектора в

масштабе равна амплитуде тока Im. При вращении вектора в положительном направлении (против направления движения часовой стрелки) с угловой скоростью ω проекции его на ось ординат выражают мгновенные значения тока i.

В связи с тем, что все расчеты проводятся с действующими значениями, на векторных диаграммах будем изображать не амплитуды тока и напряжения, а их действующие значения.

UR	I
UR		U R
	ϕi =ϕu	U R	I
Рисунок 1.54		Рисунок 1.55

С учетом изложенного для цепи с активным сопротивлением (рисунок 1.52) векторная диаграмма имеет вид, приведенный на рисунке 1.54.

Обычно оси координат не изображают. Вектор тока располагают произвольно, например, горизонтально (рисунок 1.55). Вектор напряжения при равенстве начальных фаз ϕu =ϕi пойдет параллельно

вектору тока.

Разность начальных фаз называют фазовым сдвигом. В цепи с активным со-

противлением фазовый сдвиг	между
напряжением и током равен нулю:
ϕ =ϕu −ϕi = 0 .	(1.61)

1.31 ИНДУКТИВНОЕ

СОПРОТИВЛЕНИЕ

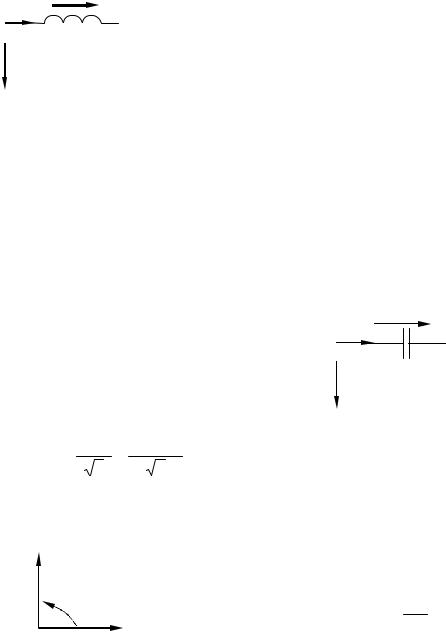
Электрическая цепь с индуктивным

U L

элементом показана

на

рисунке 1.56.

При

синусои-

дальном токе в цепи

i = I m sin(ωt +ϕi )

напряжение

на

индук-

Рисунок 1.56

тивном элементе в соот-

ветствии с (1.48):

= L

sin(ωt +ϕi ) =ωLI m cos(ωt +ϕi )

или после преобразования:

uL =U Lm sin(ωt +ϕi + 900 ) ,

(1.62)

где U Lm =ωLI m = X L I m .

Величина

X L называется индуктив-

ным сопротивлением (или реактивным со-

противлением индуктивного элемента) :

X L =ω L .

(1.63)

Индуктивное сопротивление

X L из-

меряется в омах (Ом).

Действующее значение напряжения

на индуктивном элементе:

U L =

U Lm

X L

I m

= X L I .

(1.64)

Начальная фаза напряжения соглас-

но (1.62):

ϕu =ϕi +900 ,

(1.65)

U L

то

есть

фазовый

сдвиг между

током

+ 90 0

напряжением

на

индуктивном

эле-

Рисунок 1.57

менте равен 900:

ϕ =ϕu −ϕi = 900 .

Векторная диаграмма для цепи с индуктивностью представлена на рисунке 1.57. Так как положительное направление вращения векторов принято против хода часовой стрелки, то угол + 900 на векторной диаграмме откладывается в этом направлении. Как видно из векторной диаграммы, ток отстает по фазе от напряжения на 900.

Действие индуктивного элемента в цепи синусоидального тока объясняется явлением самоиндукции.

Таким образом, цепь с индуктивностью обладает индуктивным сопротивлением, величина которого пропорциональна частоте тока. При этом индуктивный элемент вызывает отставание тока относительно напряжения на 900.

При постоянном токе индуктивное сопротивление равно нулю (так как ω = 0 ). Поэтому электротехнические устройства с индуктивными элементами, рассчитанные для работы при переменном токе, нельзя включать в сеть постоянного тока, так как при X L = 0 ток значительно увеличится по сравнению с номинальной величиной.

1.32 ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ

Электрическая цепь с ёмкостным элементом (конден- i UC сатором) представлена на рисунке

	C	1.58. Ток в цепи с
	C	конденсатором со-
U		конденсатором со-
U		гласно (1.42) возни-
		гласно (1.42) возни-
		кает при изменении
Рисунок 1.58		кает при изменении
Рисунок 1.58		напряжения:
		i = C	duc	.
		i = C		.
			dt

Напряжение на конденсаторе изменяется по синусоидальному закону:

uc =U cm sin(ωt +ϕu ) .

Сучетом этого ток в цепи с конден-

сатором:

i = C dudtc =ω CU cm cos(ωt +ϕu )

или после преобразования:

ным сопротивлением (или реактивным сопротивлением емкостного элемента):

X C =	1	.	(1.68)

	ωC
Емкостное сопротивление			X C из-

меряется в омах (Ом).

Действующее значение напряжения на основании (1.67):

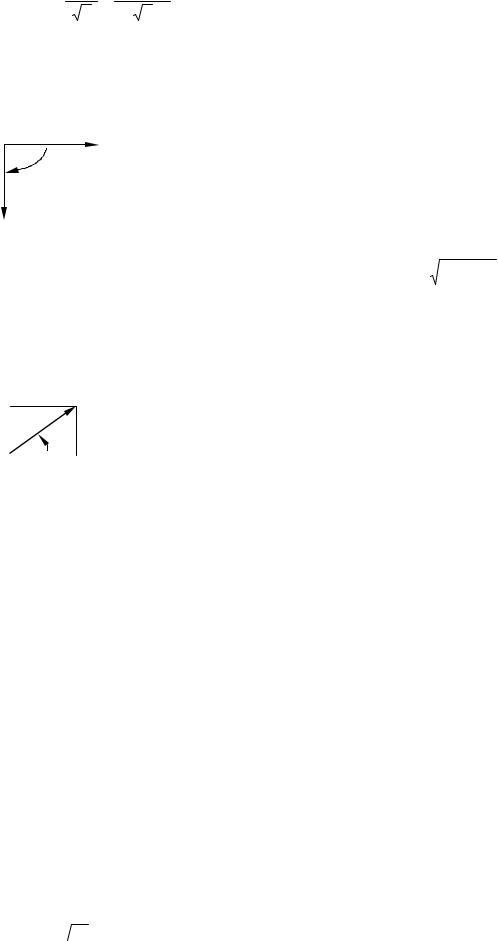
U C =	U cm	=	X C I m	= X C I .	(1.69)
	2		2

Начальная фаза тока согласно (1.66):
	ϕi	=ϕu +900 ,			(1.70)
то есть фазовый сдвиг между током					и на-
пряжением на конденсаторе равен – 900:
	I		ϕ =ϕu −ϕi = −900 .
−900			Векторная диаграмма
			представлена на рисун-

UC		ке 1.59. В цепи с иде-
UC		альным конденсатором
		альным конденсатором
	Рисунок 1.59	напряжение отстает по
	Рисунок 1.59	фазе от тока на 900.
		фазе от тока на 900.

1.33 ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ ДЛЯ

РАСЧЕТА ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА


+j			Тригонометрическая
+j	А		форма	расчета			очень
A2	А		неудобна. Поэтому для
A2			неудобна. Поэтому для
	ϕ		расчета		цепей		сину-
		+	соидального			тока при-
- 0	A1	+	меняют		так	называе-
-j			мый	символический
-j			метод. Векторы напря-
			метод. Векторы напря-
Рисунок 1.60			жения	и	тока		изобра-
Рисунок 1.60			жают на		комплексной
			жают на		комплексной

плоскости и записывают в виде комплексных чисел.

На рисунке 1.60 представлена комплексная плоскость. Ось абсцисс называют осью действительных величин (или чисел), а ось ординат – осью мнимых величин.

Составляющую вектора по мнимой оси выделяют посредством множителя j.

	Для вектора, модуль которого равен
А, можно записать:
	A = A1 + jA2 ,	(1.71.)
где	A –комплексная величина (обозна-

чается чертой снизу);

A1 – действительная часть комплексной величины;

jA2 – мнимая часть комплексной величины.

j = −1 – мнимая единица:

j 2 = −1, j3 = − j, j 4 =1,	1	= − j.
j 2 = −1, j3 = − j, j 4 =1,	j	= − j.
	j
Подста-

вимA1 = A cosϕ, A2 = A sinϕ в формулу

(1.71):

A = A cosϕ + jA sinϕ .	(1.72)
На основании формулы Эйлера
cosϕ + j sinϕ = e jϕ	(1.73)

комплексная величина (1.72) записывается в виде:

A = A(cosϕ + j sinϕ) = Ae jϕ , (1.74)

где А– модуль комплексной величины.

A = A2 + A2		,	(1.75)
1	2
ϕ – аргумент комплексной величины
ϕ = arctg	A2	.	(1.76)
ϕ = arctg	A	.	(1.76)
	A
	1

Множитель e jϕ в формуле (1.74) называют оператором поворота. Он показывает, что вектор повернут относительно положительного направления дейст– вительной оси на угол ϕ . Угол ϕ считается положительным при повороте вектора против направления движения часовой стрелки и отрицательным при повороте в обратную

сторону. Например, для ϕ = 900 :

e j900 = cos900 + j sin 900 = 0 + j1 = j .

Подобным образом:

e− j900 = − j ; e j0 =1; e j1800 = −1.

Таким образом, комплексная величена имеет три формы записи, которые называются следующим образом:

1)алгебраическая (1.71);

2)тригонометрическая (1.72);

3)показательная (1.74).

1.34КОМПЛЕКСНЫЕ ЗНАЧЕНИЯ ТОКА И

НАПРЯЖЕНИЯ В ЦЕПИ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ

Цепь с активным сопротивлением рассмотрена в п. 1.29. Схема цепи и векторная диаграмма на комплексной плоскости представлена на рисунках 1.61 и 1.62.

I	UR
I
	+	j	I
	R		I
	R		U R
U			U R
U			ϕu =ϕi
		0	ϕu =ϕi
		0		+
Рисунок 1.61		Рисунок 1.62		+
Рисунок 1.61		Рисунок 1.62

Ток и напряжение в цепи с активным сопротивлением совпадают по фазе:

ϕ =ϕu −ϕi = 0 .

Комплексное действующее значение

напряжения на активном сопротивлении в

показательной форме:

	U	R =U Re jϕu ,	(1.77)

где UR – действующее значение напряжения;

ϕu – начальная фаза напряжения.

Так как в цепи с активным сопротивлением в соответствии с формулами

(1.59) и (1.60)

UR = RI ,

ϕu =ϕi ,

то формула (1.77) запишется в виде

					U	R = RIe jϕi ,
или						R = RIe jϕi ,
или
							U	R = R I ,	(1.78)
где		U						R = R I ,	(1.78)
		U	R	–	комплексное				действующее
			R	–	комплексное				действующее
значение напряжения;
		I		–	комплексное				действующее
	значение тока:

I = Ie jϕi ,

I– действующее значение тока;

ϕi – начальная фаза тока.

1.35 КОМПЛЕКСНЫЕ ЗНАЧЕНИЯ ТОКА И

НАПРЯЖЕНИЯ В ЦЕПИ С ИНДУКТИВНЫМ СОПРОТИВЛЕНИЕМ

Цепь с индуктивным сопротивлением рассмотрена в п.1.31. Схема цепи и векторная диаграмма на комплексной плоскости представлены на рисунках 1.63 и 1.64.

Фазовый сдвиг между током и напряжением на индуктивном сопротивлении равен

ϕ =ϕu −ϕi = 900 ,

то есть вектор напряжения на комплексной плоскости повернут относительно вектора тока на 900 в положительном направлении (против направления движения часовой стрелки).

Комплексное действующее значение напряжения на индуктивном сопротивлении в показательной форме записи:

	U	L =U Le jϕu .	(1.79)

Так как в соответствии с формулами (1.64) и (1.65) в цепи с индуктивным сопротивлением

UL = X L I ,

ϕu =ϕi +900 ,

то формула (1.79) запишется в виде:

U L = X L Ie j( ϕi +900 ) = X L Ie jϕi e j 900

или

U L = jX L I ,

(1.80)

где I = Ie jϕi , e j900 = j .

						1.36 КОМПЛЕКСНЫЕ
						ЗНАЧЕНИЯ ТОКА И
						НАПРЯЖЕНИЯ В ЦЕПИ С
						ЕМКОСТНЫМ
I	UL					СОПРОТИВЛЕНИЕМ
	UL
		U L + j
	X L	U L + j			I	Цепь с емкостным сопротивлением рас-
U			+900			смотрена в п. 1.32. Схема цепи и векторная
U			+900	ϕ		26
			0	i		26
		-	0			+
		-				+
	Рисунок 1.63	Рисунок 1.64

	UC		+ j	I
	UC
I
I				ϕi


	C				+
	C			-900
U		0
U		0
			− j	UC
			− j	UC
Рисунок 1.65			Рисунок 1.66

диаграмма на комплексной плоскости представлены на рисунках 1.65 и 1.66.

Фазовый сдвиг между током и напряжением на емкостном сопротивлении равен

U = Z I .			(1.85)

Уравнение (1.85) выражает закон Ома для участка цепи в комплексной форме.

1.38 КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ ЦЕПИ ПРИ

ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ

UR	UL	UC
I
R	L	C
		C

ϕ =ϕu −ϕi = −900 ,

то есть вектор напряжения на комплексной

Рисунок 1.67

плоскости повернут относительно вектора

Для электрической цепи на рисунке

тока на 900 в отрицательном направлении.

1.67 по второму закону Кирхгофа:

Комплексное

действующее значе-

U =U R +U L +U C .

(1.86)

ние напряжения на емкостном сопротивле-

Подставим

формулу (1.86)

ком-

нии в показательной форме:

плексные значения напряжений на элемен-

C =UC jϕu .

(1.81)

тах цепи:

R = R I ,

Так как в соответствии с формулами

(1.69) и (1.70) в цепи с емкостным сопро-

U L = jX L I ,

тивлением

UC = X C I ,

C = −jX C I .

Тогда уравнение напряжений запи-

ϕu =ϕi −900 ,

шется в виде:

то формула (1.81.) запишется в виде:

= R I + jX L I − jX C I

C = X C Ie

( ϕ

−900 )

= X C Ie

jϕ

i e

− j900

или

= [R + j(X L −X C )]I = Z I ,

(1.87)

или

U C = − jX C I ,

(1.82)

где

– комплексное сопротивление

e− j900

цепи:

где I = Ie jϕi

= − j .

Z = R + j(X L −X C ).

(1.88)

1.37 ЗАКОНЫ КИРХГОФА В

Величина

КОМПЛЕКСНОЙ ФОРМЕ

X = X L −X C

Первый закон Кирхгофа:

называется реактивным сопротивлением.

Формула (1.88) представляет алгеб-

∑I n =0 .

(1.83)

раическую форму записи комплексного со-

n=1

противления.

Второй закон Кирхгофа:

Запишем Z

в показательной форме.

∑Ек =

∑Z n I n ,

(1.84)

В соответствии с уравнением (1.87):

где

E и I

к=1

n=1

Z =

jϕu

j(ϕu −ϕi )

(1.89)

– комплексные действующие

Ie jϕi

значения ЭДС и тока;

или

Z – комплексное сопротивление.

Z = Ze jϕ ,

(1.90)

Падение напряжения Z

I в (1.84)

где Z – модуль комплексного сопротив-

можно заменить напряжением U :

ления:

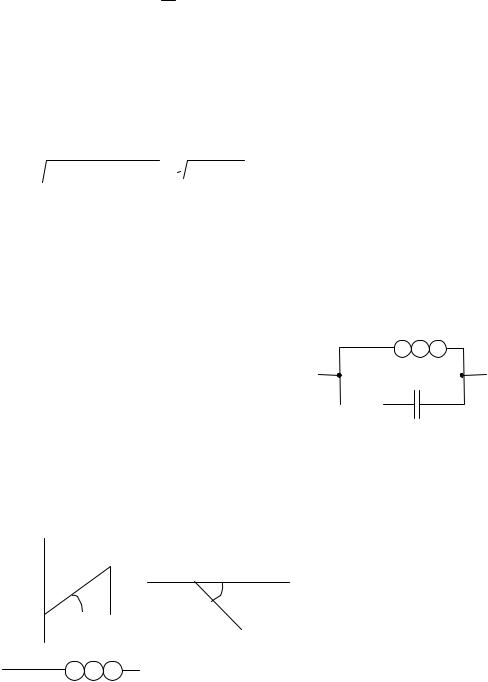
Z=UI ;

ϕ– аргумент:

ϕ=ϕu −ϕi .

Аргумент ϕ равен фазовому сдвигу между током и напряжением.

На основании (1.88) модуль и аргумент комплексного сопротивления:

В случае, когда преобладает X C над X L , реактивное сопротивление цепи будет иметь емкостный характер. Комплексное сопротивление примет вид:

Z = R − jX C = Ze− jϕ .

(1.95)

Сопротивлению (1.95) соответствует треугольник сопротивлений на рисунке 1.69.

Z = R2 + (X L − X C )2 = R2 + X 2 , (1.91)

ϕ = arctg	X	= arccos	R	.	(1.92)
	R
			Z

1.39 ТРЕУГОЛЬНИК СОПРОТИВЛЕНИЙ

По формуле Эйлера (1.73) перейдем к тригонометрической форме записи Z :

Z = Ze jϕ = Z cosϕ + jZ sinϕ . (1.93)

Здесь Z cosϕ = R – активное сопротивление;

Z sinϕ = x – реактивное сопротив-

ление.

С учетом этого сопротивление Z можно представить на комплексной плоскости с помощью треугольника сопротивлений (рисунки 1.68 и 1.69).

+ j

X L

− j

X C

X L

Рисунок 1.68

Рисунок 1.69

Если в комплексном сопротивлении

Z = R + j(X L −X C )

преобладает

X L над X C , то это значит,

что реактивное сопротивление цепи имеет индуктивный характер. Комплексное сопротивление примет вид:

Z = R + jX L = Ze jϕ .

(1.94)

Сопротивлению (1.94) соответствует треугольник сопротивлений на рисунке 1.68.

1.40 КОМПЛЕКСНАЯ ПРОВОДИМОСТЬ

Комплексная проводимость – это величина, обратная комплексному сопротивлению:

y =

(1.94)

Единицей

измерения комплексной прово-

димости

служит

X L

или

сименс

Ом

(См).

На

рисунке

Рисунок 1.70

1.70

представлена

электрическая

цепь с индуктивной ( R1,X L )

и емкостной

( R2 ,X C ) параллельными ветвями.

Комплексная

проводимость

индук-

тивной ветви:

(1.95)

Z 1

R1 + jX L

Мнимость в знаменателе устраняют умножением числителя и знаменателя на сопряженную величину.

Две комплексные величины называются сопряженными, если имеют одинаковые модули и равные по величине, но противоположные по знаку аргументы.

Сопряженный комплекс отмечают звездочкой.

Если

Z1 = Z1e jϕ1 = R1 + jX L ,

то сопряженная величина

Z*1 = Z1e− jϕ1 = R1 − jX L .

Произведение сопряженных величин равно квадрату модуля:

	Z		*		= Z	e jϕ1 Z	e− jϕ1	= Z 2	= R2	+ X 2 .
	Z	1	Z	1	= Z	e jϕ1 Z	e− jϕ1	= Z 2	= R2	+ X 2 .
28		1		1	1	1		1	1	L
28

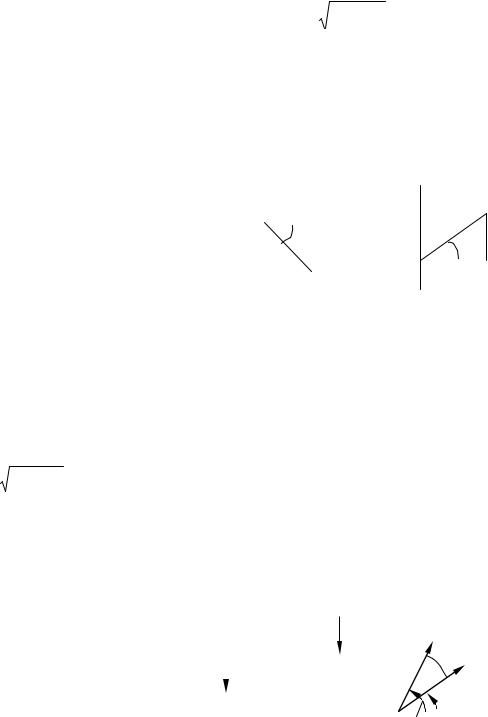
С учетом этого комплексная проводимость индуктивной ветви:

R1 − jX L

R1 + jX L

+ jX L

− jX L

R1 − jX L

R2 + X 2

y	2 = y2e jϕ2 ,	(1.105)
	2 = y2e jϕ2 ,

где y2 – модуль комплексной проводимости емкостной ветви;

ϕ2 – аргумент:

y	2	=	g2	+b2	,	(1.106)
	2		2	C

или

= g

− j b

ϕ2 = arctg

= arccos

(1.107)

(1.96)

Комплексные проводимости индук-

где

g1 – активная проводимость;

тивной и емкостной ветвей могут быть

– реактивная индуктивная прово-

представлены

с помощью треугольников

димость:

проводимостей (рисунки 1.71 и 1.72).

(1.97)

+ j

X L

(1.98)

ϕ2

R 2 +X 2

Z12

− j

В показательной форме:

= y

e− jϕ1 ,

(1.99)

Рисунок 1.71

Рисунок 1.72

где

– модуль комплексной проводи-

Эквивалентная комплексная прово-

мости;

ϕ – аргумент (фазовый сдвиг меж-

димость цепи на рисунке 1.70 равна сумме

комплексных

проводимостей ветвей

ду напряжением и током, равный разности

начальных фаз напряжения и тока в индук-

иy

тивной ветви):

э =

1 +

2 .

+b2

(1.100)

1.41 КОМПЛЕКСНАЯ

ϕ1 = arctg

= arccos

(1.101)

МОЩНОСТЬ

Определим мощность, поступаю-

Комплексная проводимость емкост-

щую в электрическую цепь (рисунок 1.73)

ной ветви рисунок (1.70) отличается от

при синусоидальных величинах тока

и на-

комплексной

проводимости

индуктивной

пряжения.

ветви (1.96) знаком:

= g2 + jbС ,

(1.102)

R2 − jX C

где

g2 – активная проводимость;

ϕi

bС

– реактивная емкостная прово-

ϕu

димость:

Рисунок 1.73

Рисунок 1.74

(1.103)

Комплексная мощность цепи определяется

2 +X C2

Z 22

через сопряженное комплексное

значение

тока:

X C

(1.104)

2 +X C2

Z 22

S =

I ,

(1.108)

В показательной форме:	где согласно рисунку 1.74
В показательной форме:
	29

U =Ue

jϕu

, I = Ie

jϕ

i ,

= Ie

− jϕ

i .

С учетом этих значений

=Ue jϕu Ie− jϕi =UIe jϕ , (1.109)

S =U I

где ϕ =ϕu −ϕi .

Выражение комплексной мощности (1.109) на основании формулы Эйлера запишем в виде:

S =UIe jϕ =UI cosϕ + jUI sinϕ

или
S = P + jQ ,	(1.110)
где действительная часть равна
P =UI cosϕ ,	(1.111)
а мнимая часть –
Q =UI sinϕ ,	(1.112)

Мощность P называется активной мощностью. Она называется также средней мощностью, так как представляет собой среднее значение мгновенной мощности

p = ui

за период:
					1 T
				P =		∫uidt =UI cosϕ
				P =	T	∫uidt =UI cosϕ
+ j					T	0
+ j						,
	S	Q		где		u =U m sinωt ,
	ϕ	Q		i = I m sin(ωt −ϕ) .

0	P		+
0	P		+				Мощность
							Мощность
Рисунок 1.75				Q (1.112) называется
Рисунок 1.75				реактивной			мощно-
				реактивной			мощно-
				стью.
	Треугольник мощностей						на ком-

плексной плоскости представлен на рисун-

ке 1.75.

Модуль комплексной мощности

Q =UI sinϕ – реактивная мощность; единица измерения вольт–ампер реактивный (ВАр).

Комплексная мощность выражается через комплексное сопротивление (рисунок 1.73) следующим образом:

комплексную мощность выражают формулой:

S = Z I 2 .

(1.114)

Подставим значение Z

Z= R + j(X L −X C )

вформулу комплексной мощности (1.114):

S =(R + jX L − jXC ) I 2 = =P + jQL − jQC =P + jQ,

где P = RI 2 – активная мощность, (Вт); QL = X L I 2 – реактивная индуктив-

ная мощность, (ВАр);

QC = X C I 2 – реактивная емкостная

мощность, (ВАр); Реактивная мощность:

Q=QL −QC .

1.42КОЭФФИЦИЕНТ

МОЩНОСТИ

Величина cosϕ , представляющая отношение активной мощности к полной, называется коэффициентом мощности. В соответствии с формулой (1.111) коэффициент мощности:

cosϕ =	P	=		P	.	(1.115)
	S
			UI

S =UI = P 2 +Q2 .

(1.113)

называется полной мощностью.

Таким образом, имеются три вида мощности цепи синусоидального тока:

S =UI – полная мощность; единица измерения вольт–ампер(ВА) или кило- вольт–ампер(кВА);

P =UI cosϕ – активная мощность; единица измерения ватт (Вт) или киловатт

(кВт);	30

Если заданы параметры цепи, то коэффициент мощности определяют на основании треугольника сопротивлений, который подобен треугольнику мощностей:

cosϕ =	R	.	(1.116)
	Z
В практической		электротехнике

стремятся к тому, чтобы cosϕ был по возможности больше. Как видно из формулы

P =UI cosϕ

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019104.96 Кб2Tehnologiya-transportnyh-processov.doc
#
21.11.2019107.52 Кб2Teil Passau aus Кравченко.doc
#
10.09.2019163.33 Кб2Tema16(konsolid).doc
#
14.02.20152.1 Mб74Teoria2.doc
#
14.02.2015989.2 Кб23teoriticheskie_osnovy_elektrotekhniki_chast2.pdf
#
14.02.20151.02 Mб22teoriticheskie_osnovy_elektrotekhniki_chast_1.pdf
#
14.02.20152.94 Mб11teoriya-Avtokad-2013.pdf
#
12.03.20164.75 Mб195terehova_vupap.pdf
#
14.02.2015275.46 Кб174Termodinamika_metodichka.doc
#
11.11.2019926.72 Кб88test фарм.doc
#
14.02.2015131.58 Кб151Testy_k_zachet2012.doc