
- •Министерство образования и науки российской федерации
- •Часть 1. Гамма-, бета- и пси-функции
- •390005, Рязань, ул. Гагарина, 59/1.
- •Предисловие
- •§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
- •Определение и простейшие свойства гамма-функции в комплексной области
- •Рассмотрим замкнутую область(см. Рис. 1.1).
- •Дальнейшие свойства гамма-функции
- •Примеры
- •Примеры на применение формулы
- •Другое интегральное представление гамма-функции и следствия из него
- •§ 2. Бета-функция Эйлера (Эйлеров интеграл 1 рода)
- •2.1. Определение и связь с гамма-функцией
- •2.2. Свойства бета–функции
- •2.3. Некоторые обозначения и символы
- •§ 3. Гамма-функция в вещественной области
- •Функциональная характеристика гамма-функции
- •3.2. График функции
- •3.3. График функции
- •4.2. Функция прии ее график
- •4.3. Дальнейшие свойства пси-функции
- •4.4. Вычисление преобразования Лапласа некоторых элементарных функций
- •4.4.1. Преобразование Лапласа функции
- •4.4.2. Преобразование Лапласа функции
3.2. График функции
Напомним, что при
![]() гамма-функция определяется формулой
гамма-функция определяется формулой![]() ;
при этом
;
при этом![]() .
Следовательно, в силу теоремы Ролля
.
Следовательно, в силу теоремы Ролля![]() Но
Но
![]()
 ,
,
![]() ,
,
следовательно,
![]() возрастает и при
возрастает и при![]()
![]() ,
а при
,
а при![]()
![]() ,
так что в точке
,
так что в точке![]() налицо минимум (см. рис. 3.1). Вычисления,
которые мы не приводим, дает
налицо минимум (см. рис. 3.1). Вычисления,
которые мы не приводим, дает![]()
Отметим еще, что
так как при
![]()
![]() ,
то функция
,
то функция![]() выпукла вниз на
выпукла вниз на![]() .
.
Далее,
![]()
![]() ,
,![]()
![]() ;
при
;
при
![]()
![]() ,
т.е.
,
т.е.
![]() при
при
![]() ;
;
![]()
Изучим теперь
![]() при
при![]() .
.
Пусть вначале
![]() .
Тогда
.
Тогда![]()
![]()
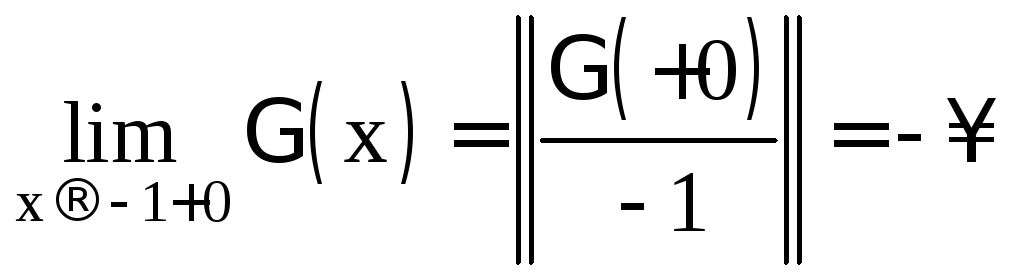 .
.
Для исследования
функции
![]() на выпуклость и вогнутость определим
знак
на выпуклость и вогнутость определим
знак![]() при
при![]() .
.
Продифференцировав формулу понижения
![]() :
:
![]() ,
,
поделим
![]() левую
часть на
левую
часть на![]() ,
а правую - на
,
а правую - на![]() :
:
![]() .
.
Дифференцируем еще раз:
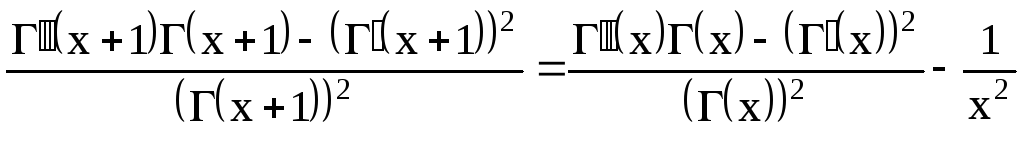 .
.
Но по доказанному выше в п. 3.1 при
![]() ,
,
следовательно,
![]() при
при![]() .
.
Применяя это
рассуждение последовательно несколько
раз, заключаем, что на каждом отрезке
вида
![]()
![]() ,
т.е.
,
т.е.![]() имеет знак
имеет знак![]() :
если
:
если![]() ,
то
,
то![]() если
если![]() ,
то
,
то![]() В частности, на каждом отрезке вида
В частности, на каждом отрезке вида![]() имеется единственная стационарная
точка
имеется единственная стационарная
точка![]() ,
причем при
,
причем при
![]() .
.
График гамма-функции приведен на рис. 3.2 жирной линией.
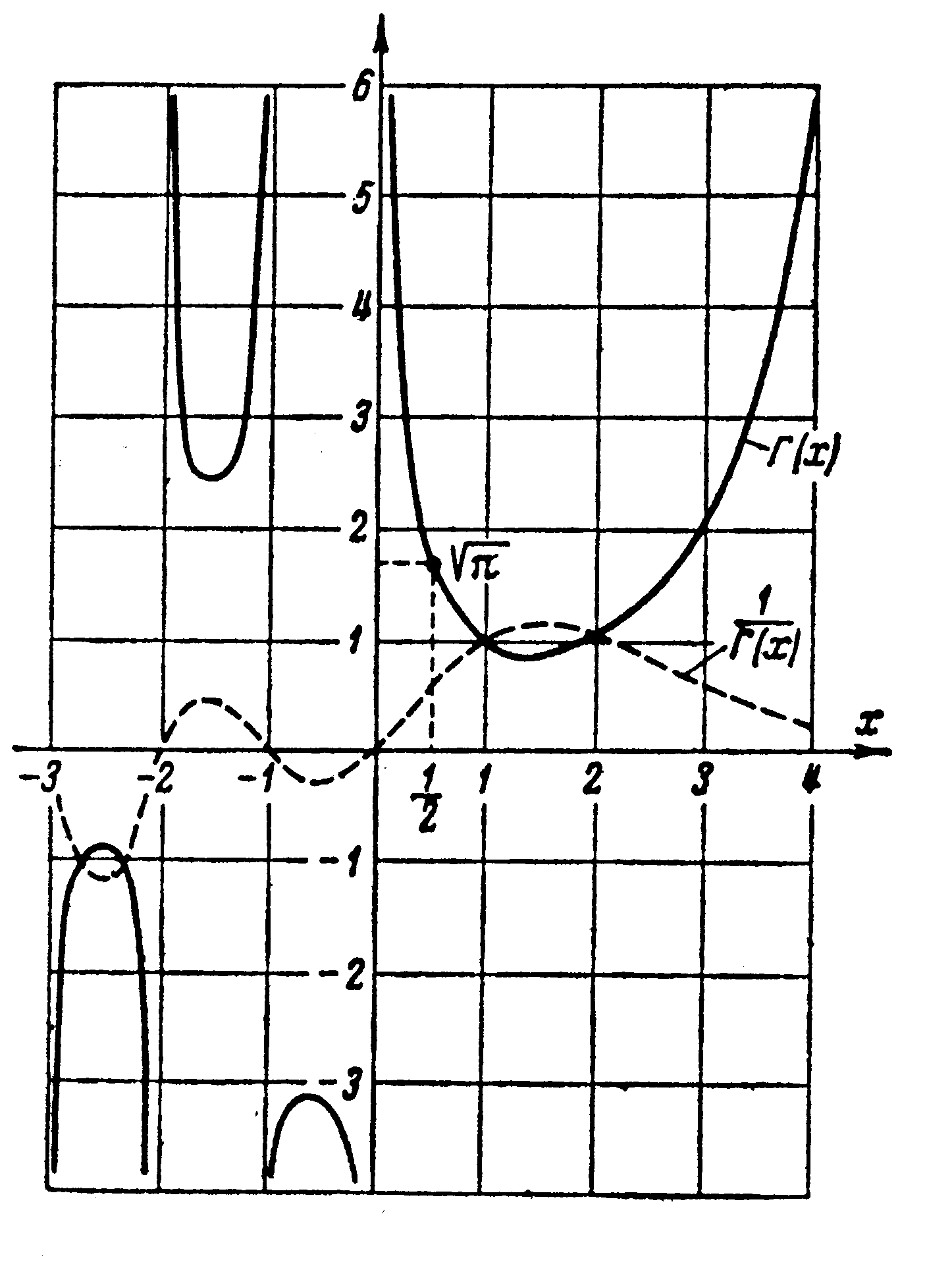
Рис. 3.2
3.3. График функции
Эта функция
определена
![]() ;
в точках
;
в точках![]() доопределим
ее естественным образом – по непрерывности.
При этом в окрестности нуля имеем:
доопределим
ее естественным образом – по непрерывности.
При этом в окрестности нуля имеем:
![]()
В окрестности
![]() :
:![]()
В окрестности
![]() :
:![]()
![]()
![]() .
.
Далее,
![]() ,
следовательно, функция
,
следовательно, функция![]() возрастает там, где
возрастает там, где![]() убывает, и наоборот.
убывает, и наоборот.
График функции
![]() приведен на рис. 3.2 пунктирной линией.
приведен на рис. 3.2 пунктирной линией.
3.4. Пример
![]() .
.
Решение.
![]()
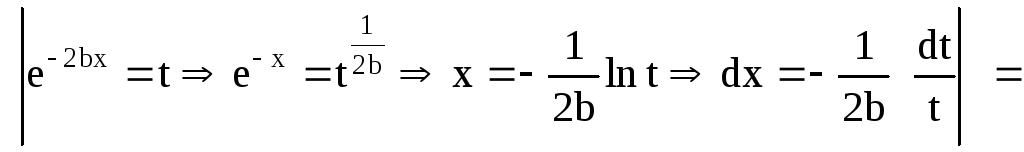
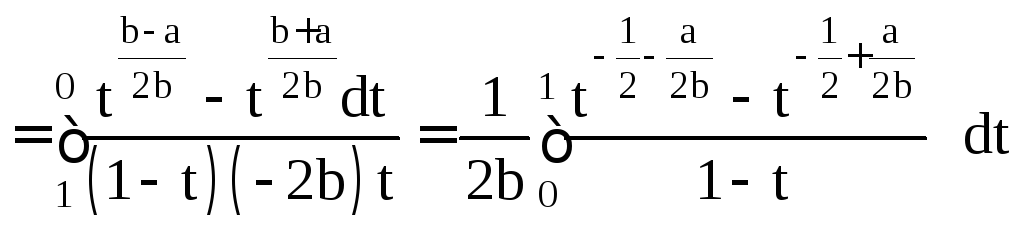 .
.
Обозначим
![]() .
Тогда
.
Тогда![]() ;
при этом
;
при этом![]() .
В этих обозначениях
.
В этих обозначениях
![]()
![]()
![]()
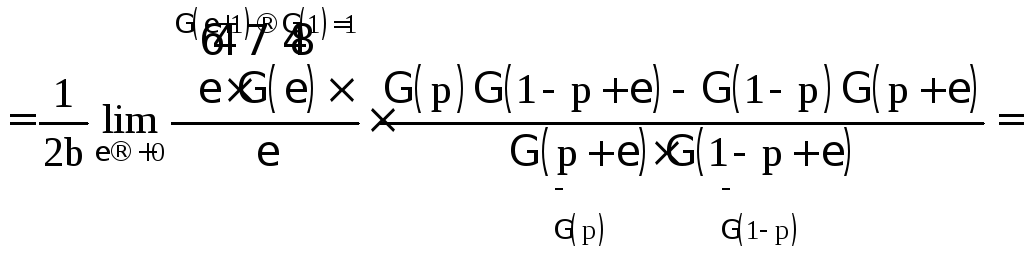
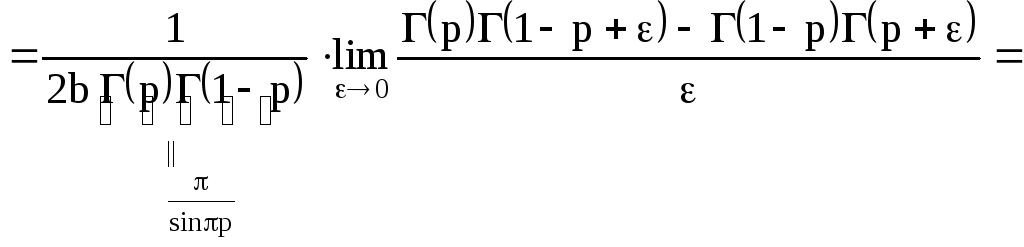
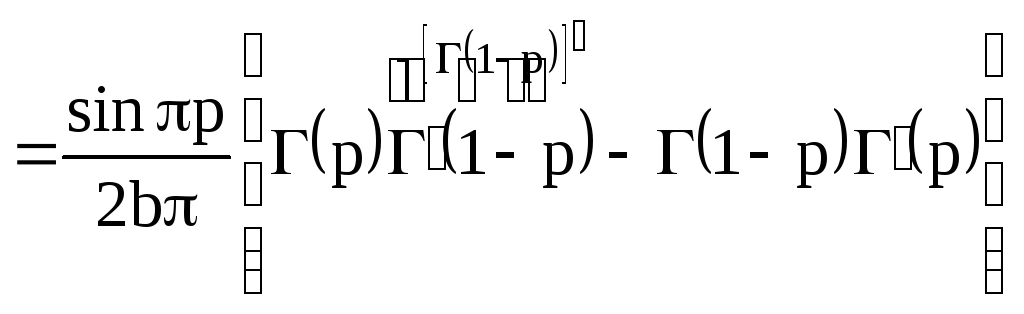 =
=
![]()
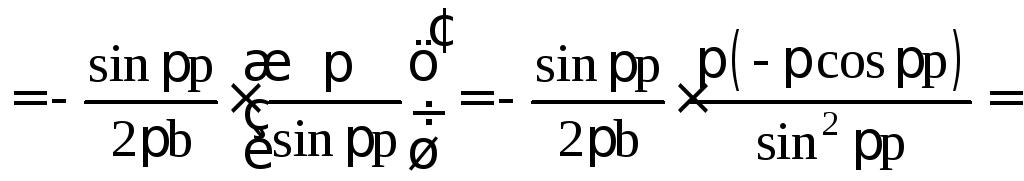
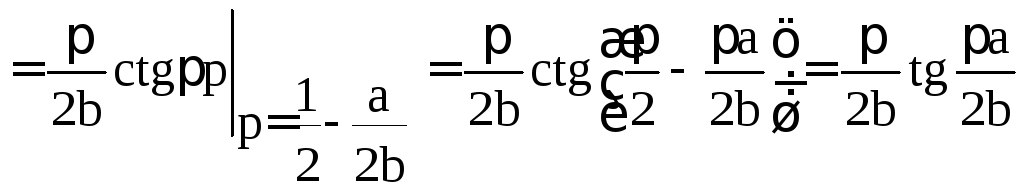 .
.
§ 4. Пси-функция
4.1. Определение и простейшие свойства
Пси-функция
![]() определяется как логарифмическая
производная Г-функции:
определяется как логарифмическая
производная Г-функции:
![]() .
.
Непосредственно
из определения следует, что функция
![]() аналитична
при
аналитична
при
![]() ,
а так как
,
а так как
![]() то
в окрестности
точки
то
в окрестности
точки
![]()
![]() ,
где
,
где
![]() - аналитическая в окрестности точки
- аналитическая в окрестности точки![]() функция. Отсюда
функция. Отсюда
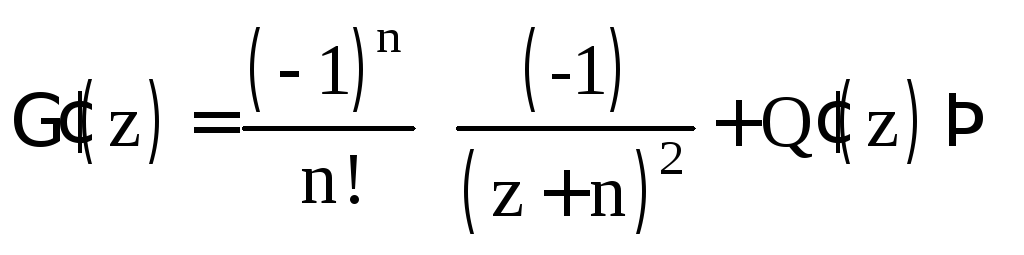

![]()
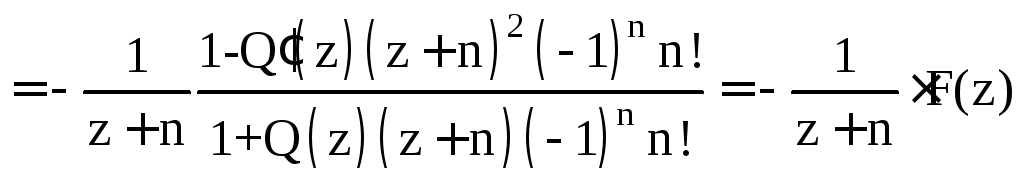 ,
,
где
![]() - аналитическая в окрестности точки
- аналитическая в окрестности точки![]() функция. Следовательно,
функция. Следовательно,
![]() -полюс 1
порядка.
-полюс 1
порядка.
Тем самым доказано
Свойство 4.1.
![]()
Свойство 4.2 (рекуррентная формула):
![]() .
.
Доказательство.
![]()
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Свойство 4.3 (формула симметрии):
![]() .
.
Доказательство.
Из формулы симметрии для гамма-функции
выразим
![]() .
Тогда
.
Тогда
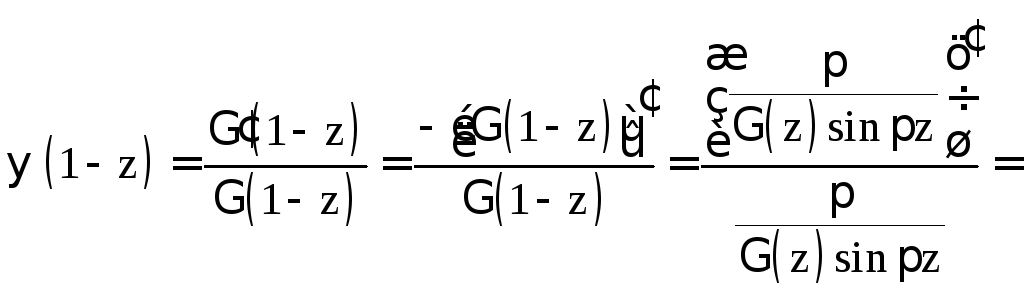
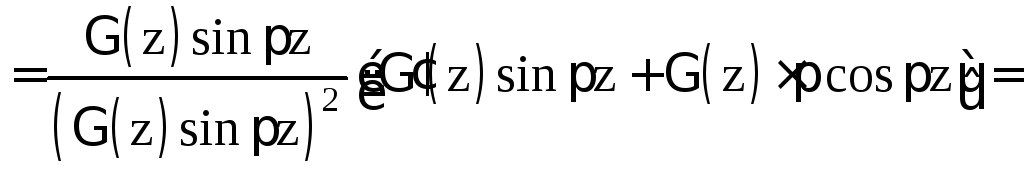
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Свойство 4.4 (формула удвоения):
![]() .
.
Доказательство.
Из формулы удвоения для гамма-функции
выразим
![]() .
Тогда
.
Тогда
![]()
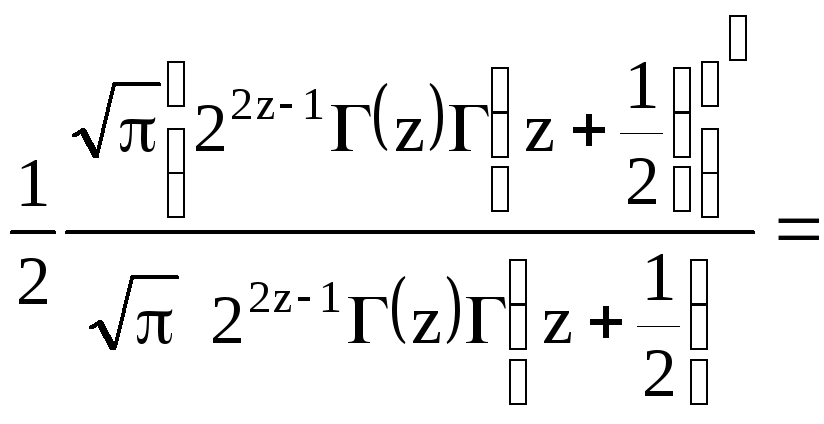
![]() ,
,
ч.т.д.
Аналогично![]() с помощью общей формулы умножения для
гамма-функции доказывается, что
с помощью общей формулы умножения для
гамма-функции доказывается, что
![]()
Замечание.
![]() имеет другое название – дигамма-функция;
в этой терминологии ее производная
имеет другое название – дигамма-функция;
в этой терминологии ее производная![]() -
тригамма-функция;
-
тригамма-функция;![]() - тетрагамма-функция;
- тетрагамма-функция;![]() - пентагамма-функция и т.д.
- пентагамма-функция и т.д.
4.2. Функция прии ее график
По определению
при
![]() .
.
Из свойств гамма-функции следует, что
![]()
![]()
![]() при
при
![]() .
.
Величина
![]() называется константой Эйлера-Маскерони
и обозначается
называется константой Эйлера-Маскерони
и обозначается![]() .
Тем самым
.
Тем самым
![]() .
.
Вычисления, которые мы не приводим, показывают, что
![]()
Далее,
 .
.
Отсюда следует,
что
![]() возрастает на
возрастает на![]() и на
и на![]() .
При этом
.
При этом
![]()
![]() .
.
Тем самым
![]()
![]() при
при![]() ,
а так как
,
а так как![]() в силу монотонности пси-функции выполнено:
в силу монотонности пси-функции выполнено:![]() ,
то
,
то![]() при
при![]() .
.
Далее, так как
![]() - полюс 1 порядка с вычетом (-1), то в
окрестности точки
- полюс 1 порядка с вычетом (-1), то в
окрестности точки![]()
![]() и при
и при![]()
![]() .
.
График пси-функции изображен на рис. 4.1.
Рис.
4.1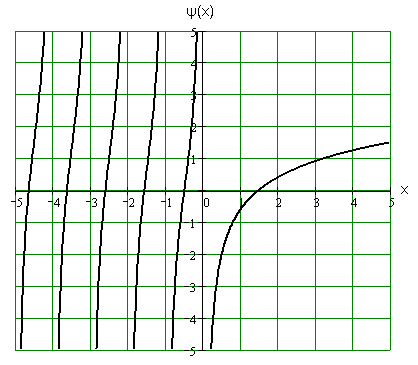
То, что
![]() при
при![]() ,
будет показано чуть ниже.
,
будет показано чуть ниже.
4.3. Дальнейшие свойства пси-функции
4.3.1. Докажем формулу
![]() .
.
Доказательство.
Известно, что точка
![]() -
полюс 1 порядка для
-
полюс 1 порядка для![]() с вычетом
с вычетом![]() т.е. в окрестности точки
т.е. в окрестности точки![]()
![]() некоторая
аналитическая функция. Следовательно,
функция
некоторая
аналитическая функция. Следовательно,
функция![]() аналитична на всей комплексной плоскости
С.
аналитична на всей комплексной плоскости
С.
Можно доказать,
что
![]()
![]() Но
Но
![]() ч.т.д.
ч.т.д.
Следствие.
![]() ,
,
где
![]() -
обобщенная дзета-функция, которая при
-
обобщенная дзета-функция, которая при![]() превращается в обычную дзета-функцию
Римана
превращается в обычную дзета-функцию
Римана![]() :
:![]() .
.
В частности,
![]() ;
;
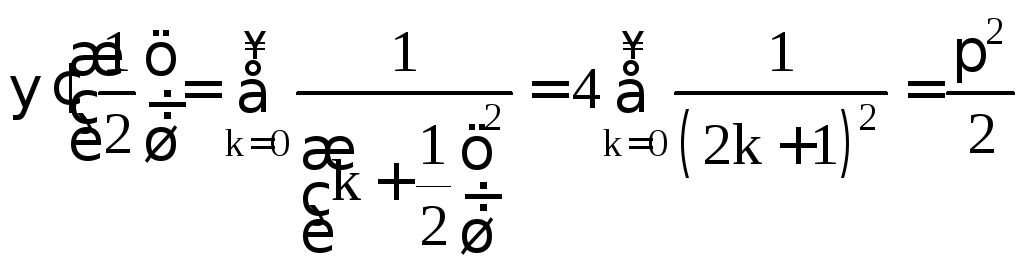 .
.
Далее,
![]()
![]() при
при
![]()
В частности,
![]() и т.д.
и т.д.
4.3.2. Выпишем далее
несколько первых коэффициентов разложения
функции
![]() в ряд по степеням
в ряд по степеням![]() :
:
![]() .
.
Но
![]() ,
,![]() ;
вычислим
;
вычислим![]() .
Имеем:
.
Имеем:
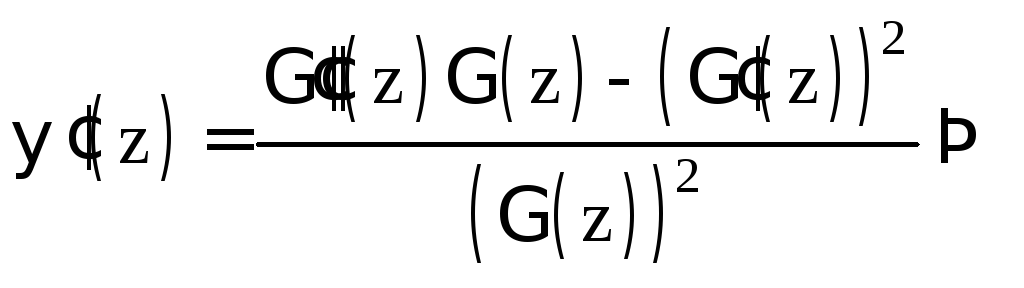
![]() .
.
Заодно найдено
значение интеграла, представляющего
![]() :
:
![]() .
.
4.3.3. Опираясь на выведенные выше в п. 1.2 формулы
понижения:
![]() ,
(4.1)
,
(4.1)
дополнения:
![]() , (4.2)
, (4.2)
и удвоения:
![]() , (4.3)
, (4.3)
а также полученные численные значения
![]() ,
(4.4)
,
(4.4)
вычислим значения пси-функции еще в некоторых точках.
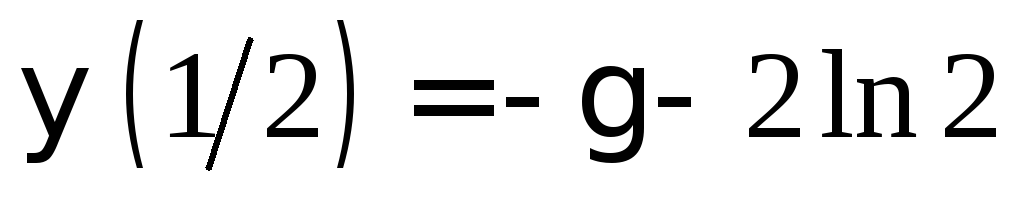 .
.
Действительно,
возьмем в (3)
![]()
![]()
![]() .
.
Следствие.
![]() .
.
Действительно,
взяв в (2)
![]() ,
получаем:
,
получаем:
![]()
Взяв в (3)
![]() ,
получаем:
,
получаем:
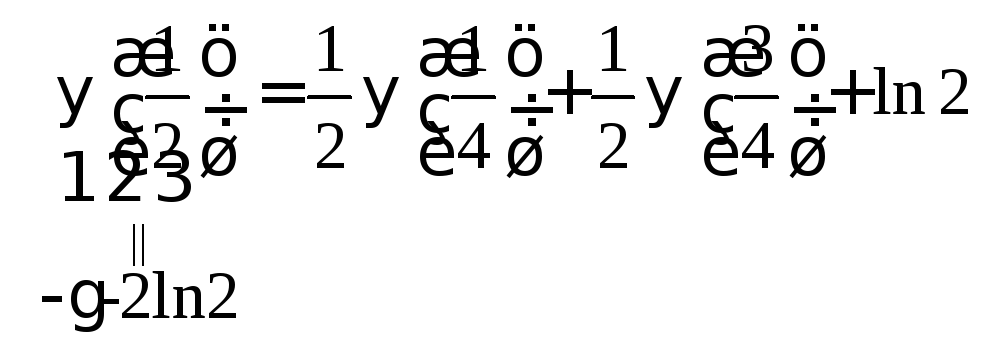
Таким образом,
задача свелась к нахождению неизвестных
![]() и
и![]() из системы
из системы
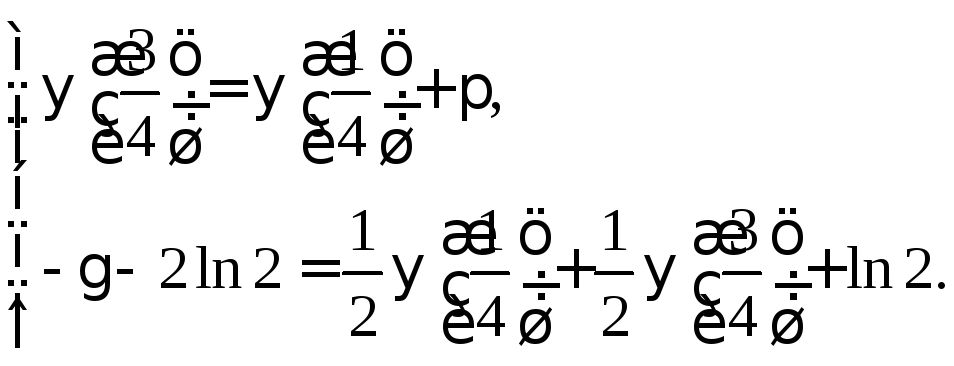
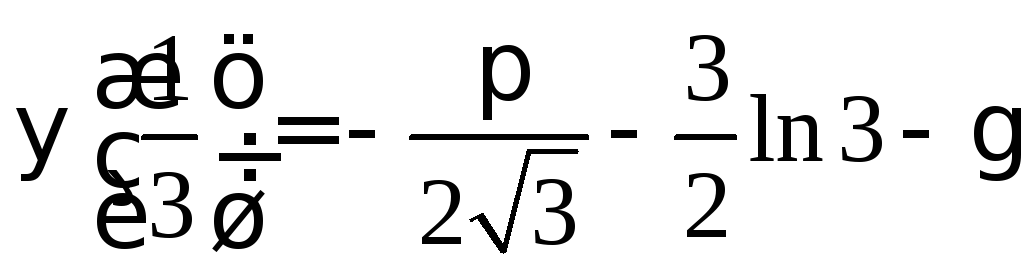 ;
;
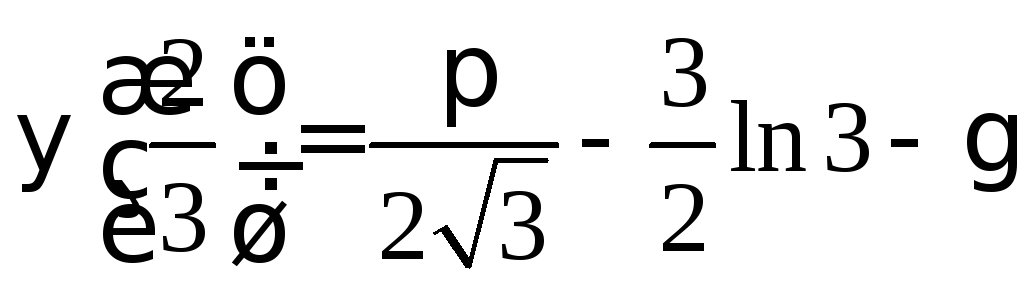
Для доказательства воспользуемся формулой утроения
![]()
Взяв здесь
![]() ,
получаем
,
получаем

![]()
Взяв в (2)
![]() ,
получаем:
,
получаем:
![]()
![]()
![]()
![]()
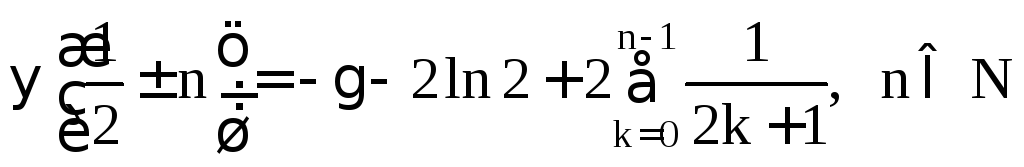 .
.
Доказательство. Согласно формуле понижения (1) имеем:
![]()
![]()
![]()
![]() ,
,
ч.т.д.
Значение
![]() найдем отсюда с использованием формулы
дополнения (2):
найдем отсюда с использованием формулы
дополнения (2):
![]()
![]()
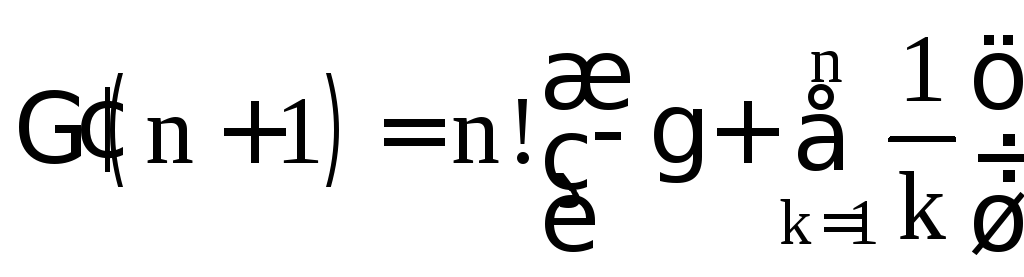 .
.
Доказательство. По определению
 ,
ч.т.д.
,
ч.т.д.
