- •Министерство образования и науки российской федерации
- •Часть 1. Гамма-, бета- и пси-функции
- •390005, Рязань, ул. Гагарина, 59/1.
- •Предисловие
- •§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
- •Определение и простейшие свойства гамма-функции в комплексной области
- •Рассмотрим замкнутую область(см. Рис. 1.1).
- •Дальнейшие свойства гамма-функции
- •Примеры
- •Примеры на применение формулы
- •Другое интегральное представление гамма-функции и следствия из него
- •§ 2. Бета-функция Эйлера (Эйлеров интеграл 1 рода)
- •2.1. Определение и связь с гамма-функцией
- •2.2. Свойства бета–функции
- •2.3. Некоторые обозначения и символы
- •§ 3. Гамма-функция в вещественной области
- •Функциональная характеристика гамма-функции
- •3.2. График функции
- •3.3. График функции
- •4.2. Функция прии ее график
- •4.3. Дальнейшие свойства пси-функции
- •4.4. Вычисление преобразования Лапласа некоторых элементарных функций
- •4.4.1. Преобразование Лапласа функции
- •4.4.2. Преобразование Лапласа функции
§ 1. Гамма-функция Эйлера (Эйлеров интеграл 2 рода)
Определение и простейшие свойства гамма-функции в комплексной области
При
![]() рассмотрим функцию
рассмотрим функцию
![]() ,
(1.1)
,
(1.1)
где
![]()
![]()
Свойство 1.1.
Функция
![]() определена и непрерывна в области
определена и непрерывна в области![]() (в
правой полуплоскости).
(в
правой полуплоскости).
Доказательство. Оценим подынтегральную функцию в (1) по модулю:
![]()
![]()
Рассмотрим замкнутую область(см. Рис. 1.1).
Пусть
![]() .
.
При
![]()
![]()
при
![]()
![]() .
.
Отсюда
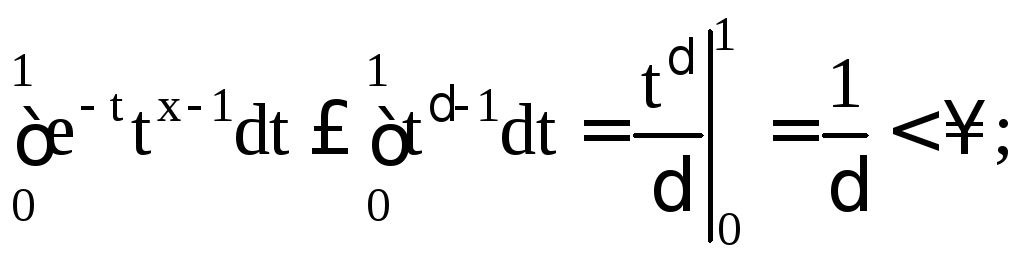 для
доказательства сходимости второго
интеграла применим интегрирование по
частям:
для
доказательства сходимости второго
интеграла применим интегрирование по
частям:
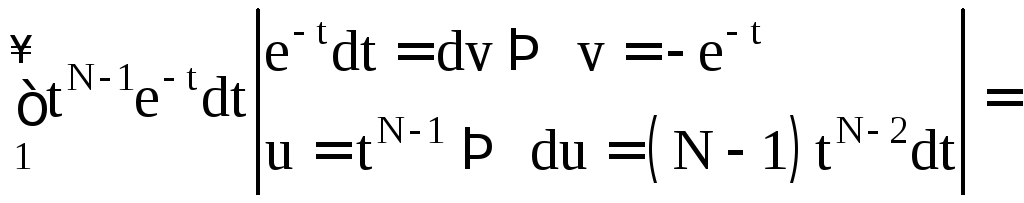
![]()
![]() .
.
Будем продолжать
интегрирование по частям до тех пор,
пока показатель степени не уменьшится
до величины
![]() ,
,![]() .
Тогда
.
Тогда
![]()
![]() .
.
Таким образом,
функция
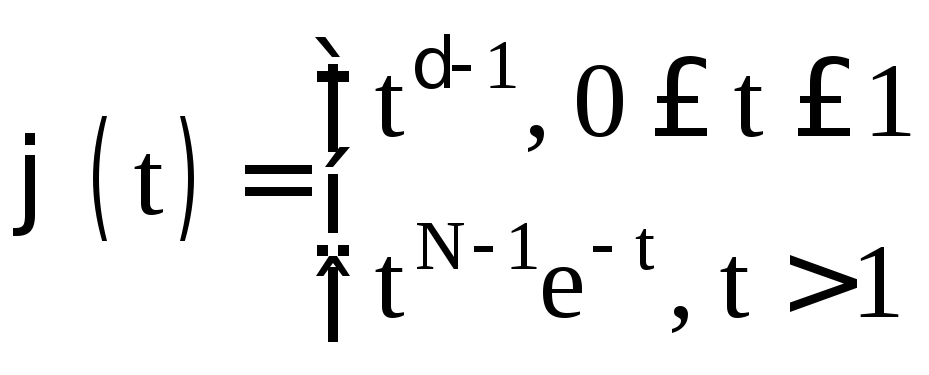 является мажорантой для
является мажорантой для![]() на
на![]() .
Поскольку интеграл
.
Поскольку интеграл![]() то интеграл
то интеграл![]() сходится равномерно относительно
сходится равномерно относительно![]() ,
следовательно, функция
,
следовательно, функция![]() определена и непрерывна в области
определена и непрерывна в области![]() и в силу произвольности
и в силу произвольности![]() и
и![]() - в области
- в области![]() ч.т.д.
ч.т.д.
Свойство 1.2.
Функция
![]() аналитична в области
аналитична в области![]() ,
причем
,
причем
![]() .
(1.2)
.
(1.2)
Доказательство.
![]()
![]() .
.
Пусть
![]() .
.
При
![]()
![]()
при
![]()
![]() интеграл
интеграл![]() сходится (см. доказательство свойства
1.1).
сходится (см. доказательство свойства
1.1).
Докажем, что
сходится интеграл
![]() .
Интегрируя по частям, получаем:
.
Интегрируя по частям, получаем:
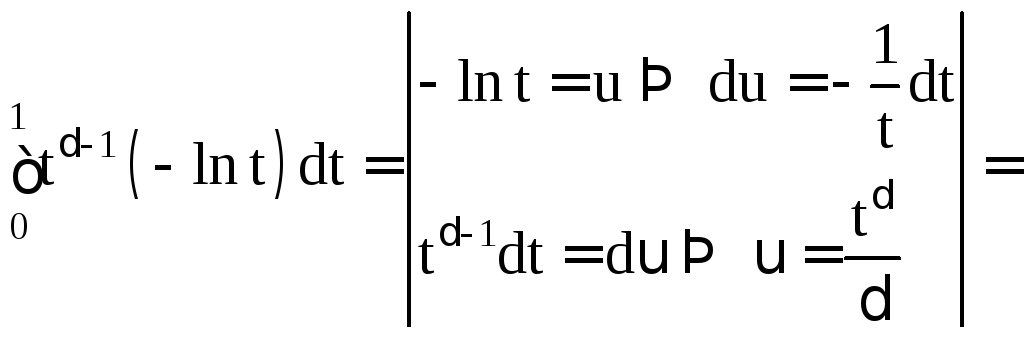
 .
.
Тем самым функция
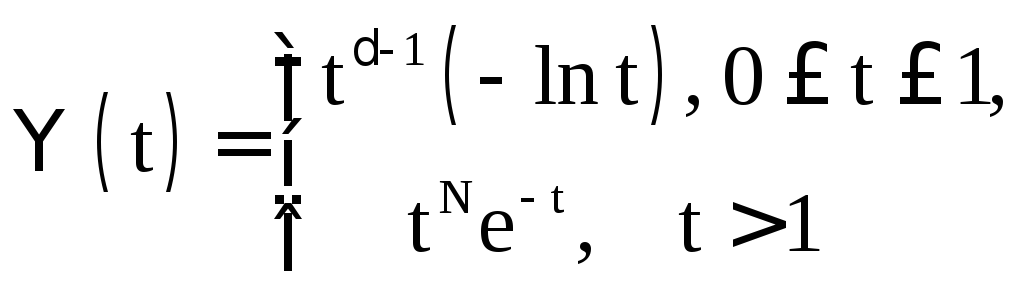 является интегрируемой мажорантой для
интеграла в правой части (2), поэтому он
сходится равномерно по
является интегрируемой мажорантой для
интеграла в правой части (2), поэтому он
сходится равномерно по
![]() ,
правило Лейбница дифференцирования
интеграла по параметру применимо, и
формула (2) доказана.
,
правило Лейбница дифференцирования
интеграла по параметру применимо, и
формула (2) доказана.
Свойство 1.3.
![]() из области
из области![]() выполняется тождество
выполняется тождество
![]()
(формула понижения; рекуррентная формула).
Доказательство. Интегрируя по частям, получаем:
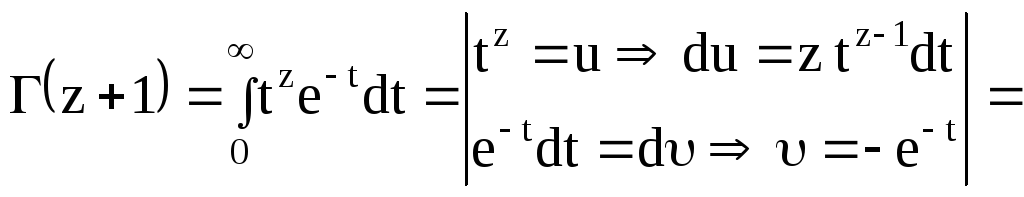
![]() ,
,
причем внеинтегральное
слагаемое обращается в ноль, так как
при
![]() при
при![]() .
Тем самым
.
Тем самым
![]() ч.т.д.
ч.т.д.
Следствие 1.
![]() .
.
Отсюда по
рекуррентной формуле получаем
![]()
![]()
![]() и т.д. В общем случае
и т.д. В общем случае
![]()
![]()
Задача.
Вычислить значения
![]()
![]() и
и![]() непосредственно.
непосредственно.
С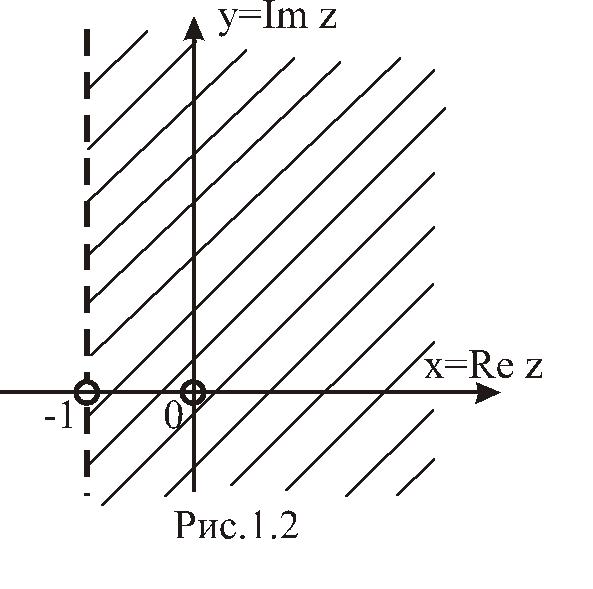 ледствие
2. Из формулы
понижения следует, что
ледствие
2. Из формулы
понижения следует, что
![]() , (1.3)
, (1.3)
при этом левая
часть (3) определена при
![]() ,
а правая – при
,
а правая – при![]() ,
т.е. при
,
т.е. при
![]() (см. рис. 1.2). Тем
самым формула (3) позволяет продолжить
функцию
(см. рис. 1.2). Тем
самым формула (3) позволяет продолжить
функцию
![]() как аналитическую в полуплоскость
как аналитическую в полуплоскость![]() ;
при этом
;
при этом![]() ,
,
т.е. точка
![]() - полюс, а так как
- полюс, а так как
![]() ,
,
то
![]() - полюс 1 порядка, т.е. в окрестности нуля
- полюс 1 порядка, т.е. в окрестности нуля
![]() ,
,
причем вычет
![]() .
.
А налогично
налогично
![]()
![]()
![]()
и функция
![]() продолжается как аналитическая в
полуплоскость
продолжается как аналитическая в
полуплоскость (см. рис. 1.3) и т.д.
(см. рис. 1.3) и т.д.
Тем самым справедливо следующее утверждение.
С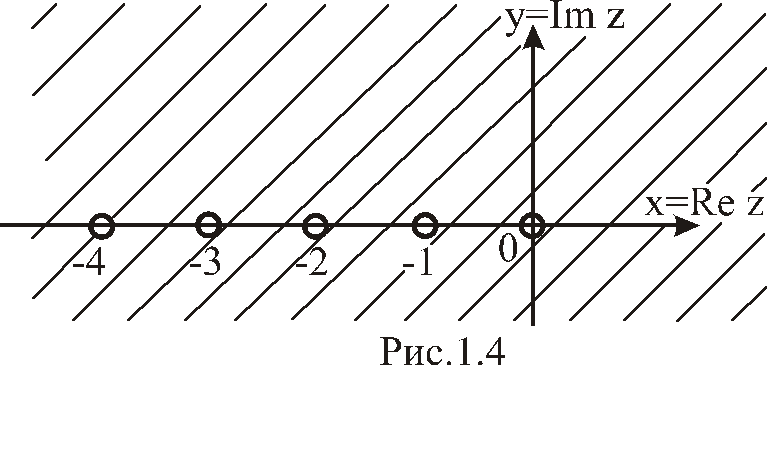 войство
1.4. Функцию
войство
1.4. Функцию
![]() можно аналитически продолжить на всю
плоскость переменной
можно аналитически продолжить на всю
плоскость переменной![]() ,
кроме точек
,
кроме точек![]() (см. рис. 1.4), в которых
(см. рис. 1.4), в которых![]() имеет полюса первого порядка с вычетами
имеет полюса первого порядка с вычетами
![]() .
.
Доказательство.
Применяя формулу понижения
![]() раз, получаем:
раз, получаем:
![]()
![]()
Правая часть определена при
![]()
при этом![]() и
и
![]()
 ,
ч.т.д.
,
ч.т.д.
Свойство 1.5.
![]()
![]()
Доказательство.
При
![]()
![]()
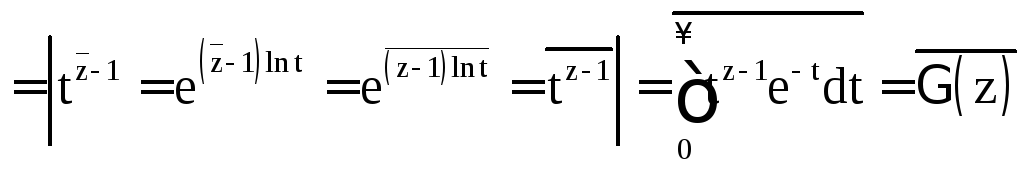 ;
;
при
![]() эта формула справедлива в силу
аналитического продолжения, а при
эта формула справедлива в силу
аналитического продолжения, а при![]()
Наглядное
представление о поведении гамма-функции
дает ее рельеф, т.е. график функции
![]() ,
приведенный на рис. 1.5. Ярко выраженные
пики над точками
,
приведенный на рис. 1.5. Ярко выраженные
пики над точками![]() соответствуют
полюсам. Два семейства линий на поверхности
представляют собой семейства линий
равного модуля и равного аргумента;
цифровые отметки на них указывают
значение модуля и аргумента (последние
– в градусах).
соответствуют
полюсам. Два семейства линий на поверхности
представляют собой семейства линий
равного модуля и равного аргумента;
цифровые отметки на них указывают
значение модуля и аргумента (последние
– в градусах).
Р ис.
1.5
ис.
1.5
Дальнейшие свойства гамма-функции
Выведем далее одну
формулу, которая понадобится нам в
дальнейшем. Для этого при
![]() рассмотрим произведение
рассмотрим произведение
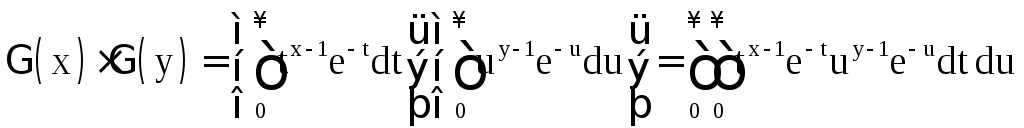
и сделаем в получившемся двойном интеграле замену переменных
![]()
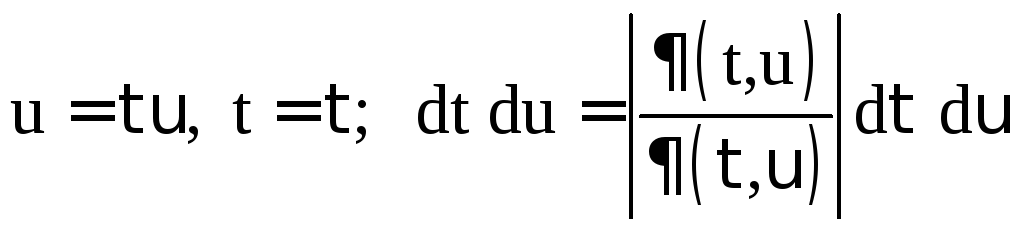 .
.
Якобиан этой замены
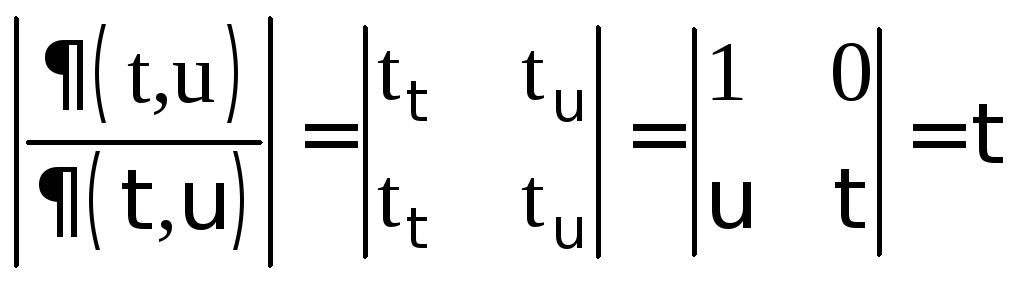 ,
,
следовательно,
![]()
 .
.
![]() Сделаем
во внутреннем интеграле замену переменной
Сделаем
во внутреннем интеграле замену переменной
![]()

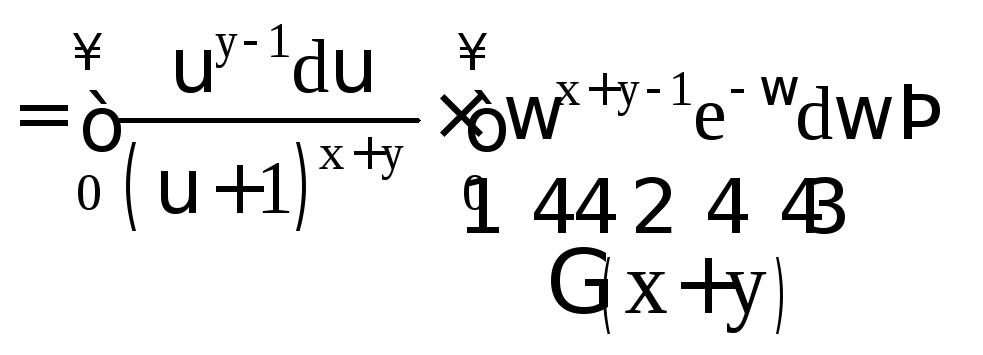
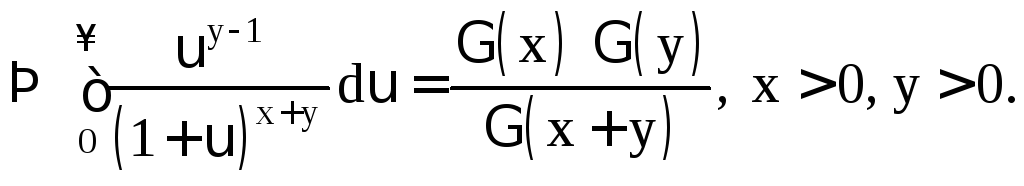 (1.4)
(1.4)
Взяв, в частности,
![]() получим
получим
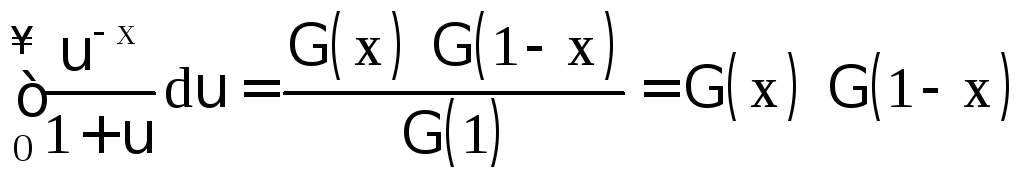 .
.
В курсе ТФКП с помощью вычетов доказывается, что при
![]()
![]() .
.
Тем самым установлено,
что при
![]()
![]()
Отсюда с помощью
аналитического продолжения заключаем,
что
![]() .
.
Покажем, что эта
формула справедлива
![]() .
Действительно, при
.
Действительно, при![]() правая часть превращается в
правая часть превращается в![]() ,
а левая принимает вид
,
а левая принимает вид![]()
Если
![]() ,
то
,
то![]() ;
если же
;
если же![]() ,
то
,
то![]() .
В обоих случаях произведение
.
В обоих случаях произведение![]() также
обращается в
также
обращается в![]() .
.
Таким образом, доказано следующее утверждение.
Свойство 1.6.
![]() (1.5)
(1.5)
(формула дополнения; формула симметрии).
Следствие.
При
![]() произведение
произведение![]() выражается через элементарные функции.
выражается через элементарные функции.
Доказательство. Пусть вначале
![]()
![]()
![]()
![]()
Для остальных n доказательство аналогично.
Свойство 1.7.
![]() не имеет нулей:
не имеет нулей:![]()
Доказательство
проведем методом «от противного». Пусть
![]() При этом
При этом![]() ,
так как
,
так как![]() ;
а также
;
а также![]() ,
так как
,
так как![]() .
Тем самым
.
Тем самым![]()
![]() .
.
Но согласно формуле дополнения
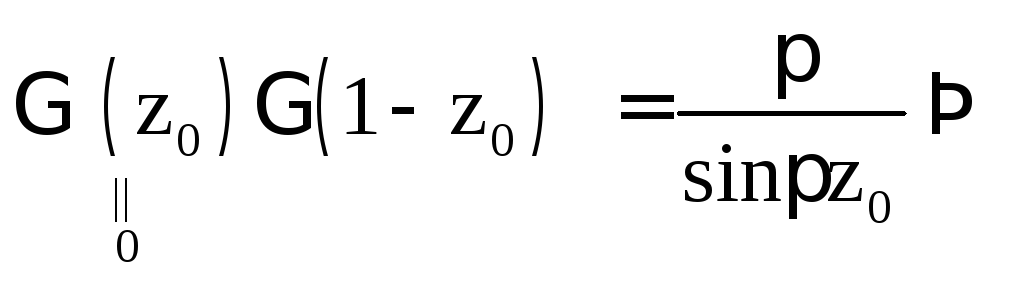
![]() т.е.
т.е.
![]()
![]() - противоречие.
- противоречие.
Следствие.
Функция
![]() - аналитическая в С.
- аналитическая в С.
На рис. 1.6. приведен
ее рельеф, т.е. график функции
![]() .
.
Р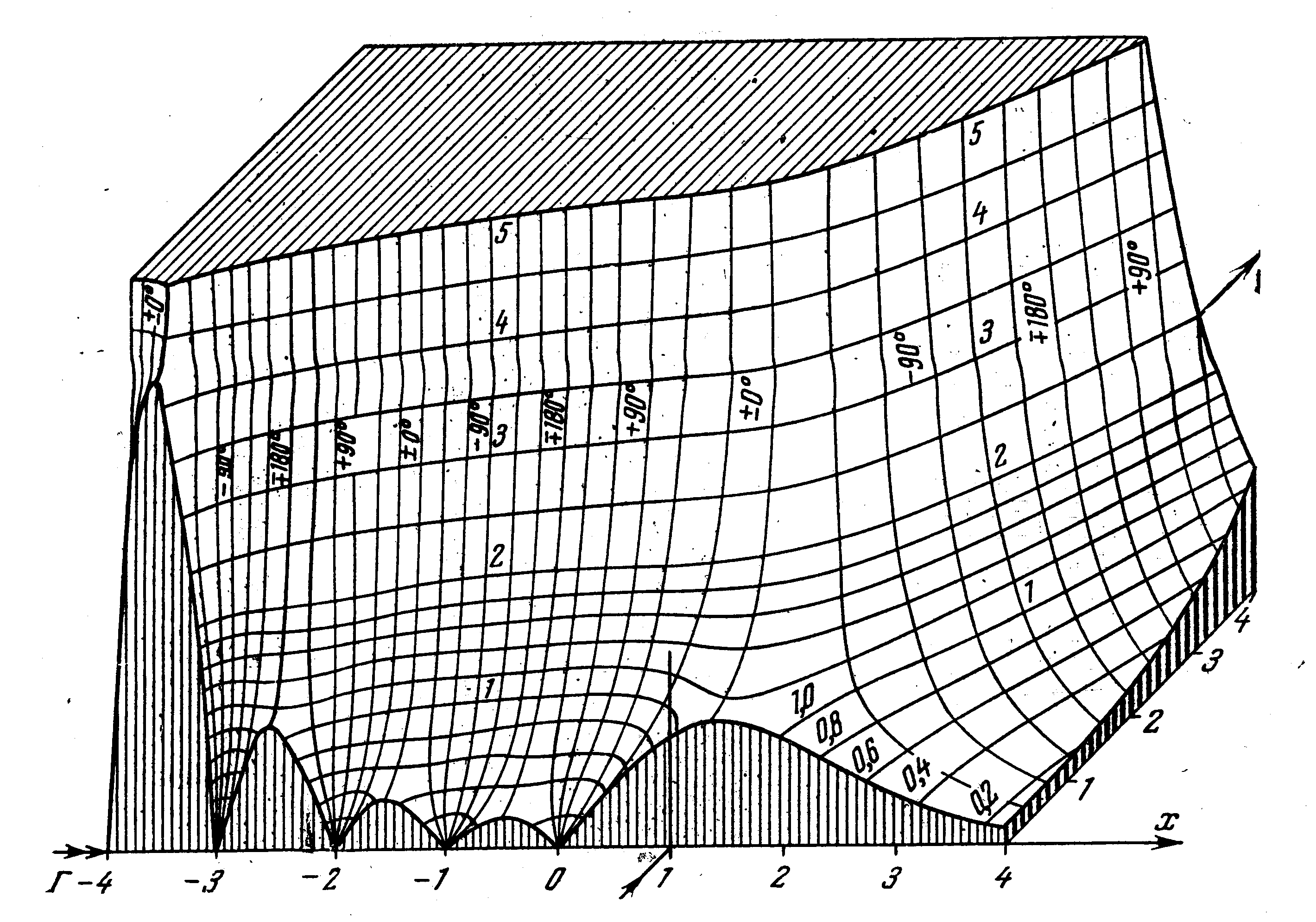 ис.
1.6
ис.
1.6
Свойство 8.
Значения
![]() в некоторых точках
в некоторых точках
Напомним, что при
![]() гамма-функция задается интегралом
гамма-функция задается интегралом![]() причем при
причем при![]() выше, исходя из определения найдено,
что
выше, исходя из определения найдено,
что![]() .
.
Вычислим далее
![]() .
.
Исходя из определения, эту величину найти не удается, так как уже значение
![]()
представляется
неберущимся интегралом. Однако ее можно
вычислить по свойствам. Так, взяв в
формуле дополнения
![]() получаем
получаем

![]() Далее,
с помощью формулы понижения получаем
Далее,
с помощью формулы понижения получаем
![]()
![]() и т.д.
и т.д.
В общем случае при
![]()
![]()
![]() .
.
Запишем это выражение через обычные факториалы:
![]()
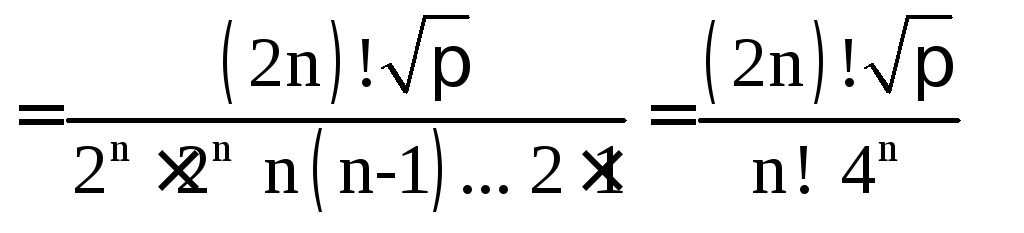 .
.
Таким образом, получаем, что
![]()
![]() .
(1.6)
.
(1.6)
Найдем далее
![]() .
.
Подставив в формулу
дополнения
![]()
![]() и пользуясь (6), получаем:
и пользуясь (6), получаем:
![]()