2.3. Некоторые обозначения и символы
.
В этих обозначениях
В § 1 было доказано, что
.
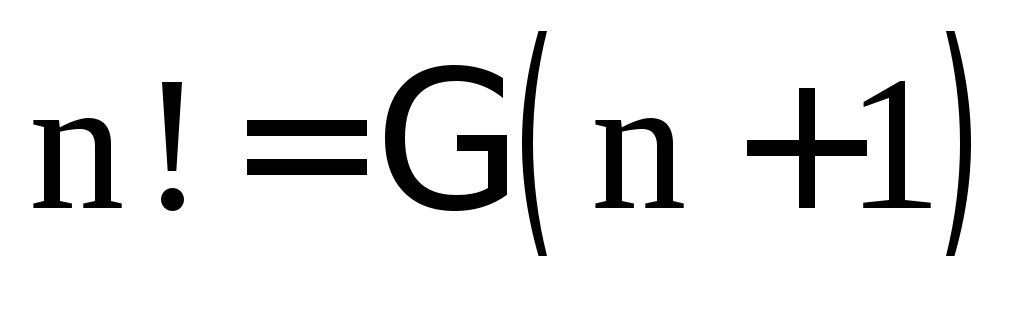Иногда наряду с гамма-функцией
рассматривают близкую к ней
.
Так как при этом
,
то именно
-функцию
естественно считать продолжением
факториала в комплексную область.
можно определить
величину
,
которую естественно считать продолжением
биномиальных коэффициентов в комплексную
область.
Для
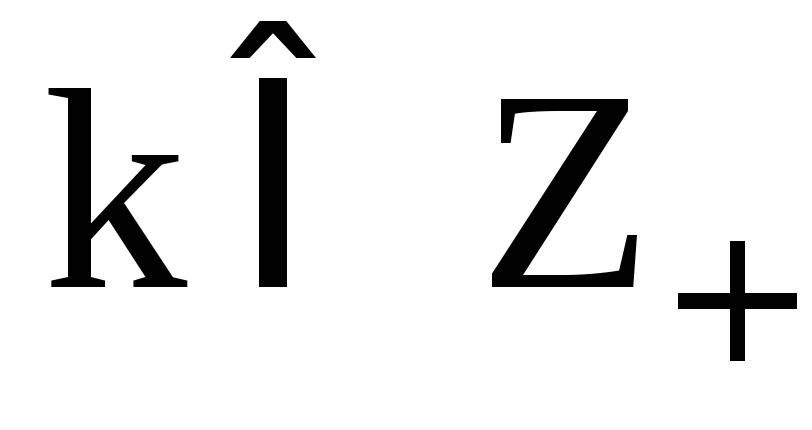символ Похгаммера
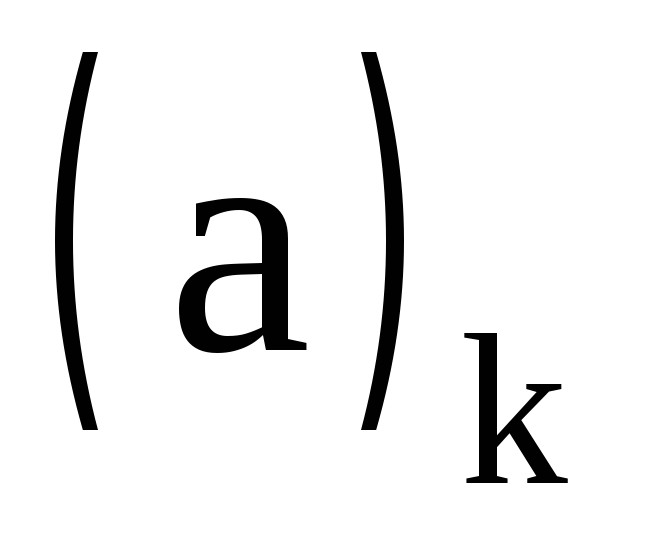определяется следующим образом:
;
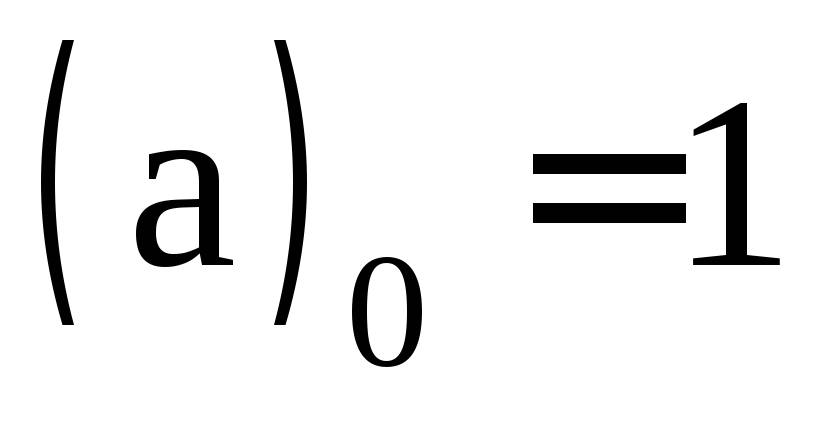при
.
Последняя формула,
во-первых, позволяет для всех
записать символ Похгаммера единообразно
и, во-вторых, естественным образом
продолжить его в комплексную область
формулой
.
Символ Похгаммера позволяет компактно записывать некоторые формулы, например, бином Ньютона:
.
§ 3. Гамма-функция в вещественной области
Функциональная характеристика гамма-функции
Многие функции однозначно определяются своими характерными свойствами. Например, хорошо известны функциональные уравнения, однозначно определяющие элементарные функции.
Теорема 1.
Если
и
то
.
Теорема 2.
Если
,
и
то
Теорема 3.
Если
и
то
.
Теорема 4.
Если
,
и
то
.
Теорема 5.
Если
,
и
то
или
.
Возникает естественный вопрос: нельзя ли и гамма-функцию однозначно определить какими-либо ее свойствами?
Мы знаем, что
функция
непрерывна вместе со своей производной
для положительных значений аргумента.
Кроме того, она удовлетворяет следующим
функциональным уравнениям:
,
(3.1)
,
(3.2)
.
(3)
Утверждается, что
эти свойства в совокупности вполне
характеризуют функцию
(так что каждая функция, обладающая
этими свойствами, тождественна с
).
Заметим, что одних
свойств (1) и (2) для этого недостаточно,
так как, наряду с
,
ими обладает и функция
(при
).
Точно так же недостаточно и свойств (2) и (3), ибо они принадлежат и функции
(при
).
Наконец, свойства
(1) и (3) явно оставляют произвольными
значения функции
для
.
Иначе обстоит дело, если налицо все три
свойства. Впрочем, свойство (3) можно
заменить более слабым требованием,
чтобы функция
при
не обращалась в ноль, что как раз и
вытекает из (3). А именно, справедливо
следующее утверждение.
Теорема
3.1. Если
функция
,
отлична от нуля и удовлетворяет
соотношениям (1) и (2):
и
то
.
Можно дать более простую характеристику гамма-функции, используя лишь одно функциональное уравнение (1), но налагая на функцию еще и требование логарифмической выпуклости.
Напомним, что
положительная функция
,
заданная на интервале
,
называется логарифмически выпуклой на
этом промежутке, если ее логарифм
оказывается выпуклой функцией.
Так как
,
то из логарифмической выпуклости функции
вытекает ее выпуклость; обратное
заключение, вообще говоря, неверно.
Таким образом, логарифмически выпуклые
функции составляют лишь часть всего
класса выпуклых функций.
Для функции
имеем:
.
Докажем, что при
справедливо неравенство
.
(3.4)
Действительно,
при
имеем:
.
Отсюда
и (4) превращается в
.
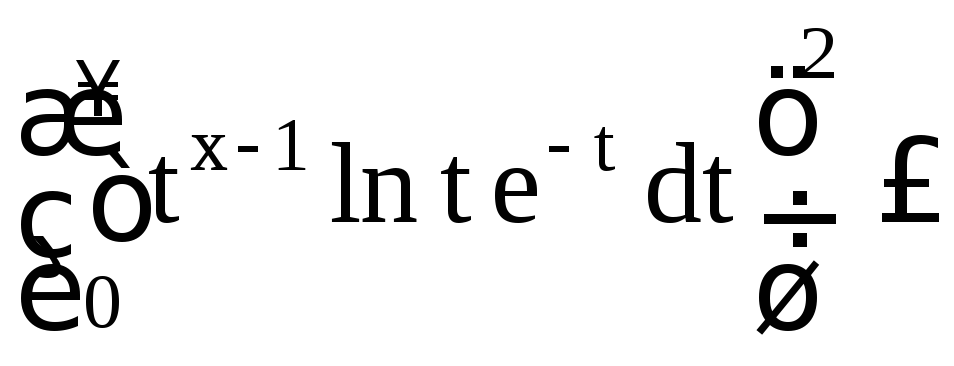
(3.5)
Возьмем в неравенстве Коши-Буняковского
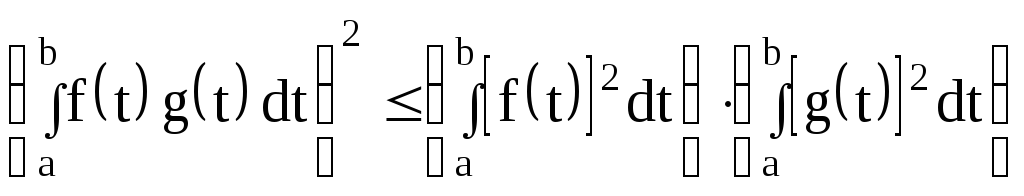(3.6)
.
Тогда
и (5) вытекает из
(6) при
и
.
Тем самым для
функции
при
справедливо неравенство
,
т.е.
выпукла вниз и
логарифмически выпукла.
Вот этим-то
свойством, совместно с уравнением (1),
функция
и определяется с точностью до постоянного
множителя.
Теорема 3.2. Если
при
и
I.
,
II.
логарифмически выпукла,
III.
,
то
.