из электронной библиотеки / 364183257333934.pdf

Функции, их свойства и графики Понятие функции. Область определения функции. Область значения

функции. Основные свойства функций. Графики элементарных функций. Преобразование графиков.

Цель: формирование умений обобщать, сравнивать, строить графики, исследовать функции.

Функция – математическое понятие, отражающее связь между элементами множеств. Более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины.

Обычно рассматриваются числовые функции, которые ставят одни числа в соответствие другим. Такие функции обладают рядом отличительных свойств и удобно представляются на рисунках в виде графиков или в виде таблиц (примером такой таблицы может быть таблица логарифмов).

Свойства:

1)Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения

41

выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называетсяпериодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции, можно исследовать функцию и по свойствам функции сможете построить график функции.

Практическая работа. Показательная функция (экспонента), ее свойства и график. Логарифмическая функция, ее свойства и график.

Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат. Свойства и графики функций y=sinx и y=cosx

Решение задач: свойства функций y=sinx, y=cosx Свойства и графики функций y=tgx и y=ctgx

Задания для самостоятельной работы. Подготовить сообщения по темам: История возникновения логарифма

Тригонометрические функции. История возникновения.

Раздел 4. Начала математического анализа

Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.

Понятие о непрерывности функции. Приращение функции. Понятие о производной. Правила дифференцирования. Производная сложной функции. Применение производной к исследованию функции.

Наибольшее и наименьшее значение функции Интегрирование как операция, обратная дифференцированию.

Вычисление интеграла

42

Цель: формирование первичных навыков дифференциального и интегрального исчислений. Сформировать умения применять производную к исследованию функции.

Практическая работа.

1.Используя правила дифференцирования, найти производную функций:

Y=5x2; y=3x7; y=3x4*z5; y= ; y= ; y=2cosx; y=sin25x

2.Найдите критические точки функций:

а) f(x)= 4 - 2x + 7x2 б) f(x)= 4x - x3/3

3.На рисунке изображен график функции у = f (х), определенной на интервале (−6; 8). Определите:

1.Количество целых точек, в которых производная функции отрицательна;

2.Количество точек, в которых касательная к графику функции параллельна прямой у = 2;

3.Количество точек, в которых производная равна нулю;

Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (−6; –3), (0; 4,2), (6,9; 8). В них содержатся целые точки −5, −4, 1, 2, 3, 4, и 7. Получили 7 точек.

2.Прямая y = 2 параллельная оси ох. Касательная будет параллельна прямой y = 2 только в точках экстремума (в точках, где график меняет своё поведение с возрастания на убывание или наоборот). Таких точек четыре: –3; 0; 4,2; 6,9

3.Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Определите количество целых точек, в которых производная функции положительна.

4.Схема исследования функции. Найти область определения функции.

Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.

Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.

Найти производную функции и ее критические точки.

43

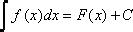
Найти промежутки монотонности и экстремумы функции.

Построить график функции, используя полученные результаты исследования. Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].

Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;

Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) Из найденных значений выбрать наибольшее и наименьшее.

Исследовать функцию

(х)= x4-2х2

Практическая работа. Интегрирование как операция, обратная дифференцированию. Вычисление интеграла.

Выше мы рассмотрели основную задачу дифференциального исчисления - нахождение производной для любой заданной дифференцируемой функции. Обратной к этой задаче является основная задача интегрального исчисления - задача восстановления функции по ее заданной производной. Такие задачи называются обратными друг к другу или взаимообратнымиИнтегрирование вводится как операция, обратная дифференцированию, но в отличие от последней приводит к неоднозначному результату: все непрерывные функции имеют бесконечно много первообразных. Следует усвоить основные методы интегрирования: метод разложения, метод замены переменной и интегрирования по частям. Среди многочисленных приложений определенного интеграла выделим классическую задачу о вычислении площади плоской фигуры.

Функция F(x) называется первообразной функции f(x) на интервале если F(x) дифференцируема на (a,b) и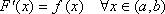

Множество всех первообразных функции f(x) на (a,b) называется неопределенным интегралом от функции f(x) на этом интервале и обозначается

Теорема. Если F(x) - первообразная f(x) на промежутке X, то любая другая ее первообразная на этом промежутке может быть записана в виде F(x)+C то есть она отличается от F(x) на постоянное слагаемое; их графики параллельны.

Неопределенным интегралом от функции f(x) называется совокупность всех первообразных f(x) . Обозначается неопределенный интеграл в виде .

Здесь функция f(x) называется подынтегральной функцией; переменная x - интегральная переменная (переменная интегрирования), f(x),dx - подынтегральное выражение, f(x) - подынтегральная функция.

Пользуясь знанием производной функции F(x), можно находить ряд несложных интегралов.

Для вычисления неопределенного интеграла мы должны, если это возможно, привести его к табличным интегралам. Рассмотрим основные приемы интегрирования.

Метод разложения.

44

Метод подстановки (метод введения новой переменной)

Данный метод состоит в том, что в интеграле 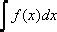, нахождение которого затруднительно, вводят новую переменную t, связанную с переменной x соотношением

где 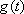– непрерывная строго монотонная функция, имеющая непрерывную производную на некотором интервале изменения , после чего получают

Метод интегрирования по частям. Пусть и – непрерывно дифференцируемые функции аргумента . На основании формулы дифференциала произведения имеем

Отсюда

Раздел 5. Геометрия. Прямые и плоскости в пространстве. Взаимное расположение прямых и плоскостей. Параллельность прямых и

плоскостей. Углы между прямыми и плоскостями.

Координаты и векторы. Координаты и векторы в пространстве. Скалярное произведение векторов. Перпендикулярность прямых и плоскостей. Многогранники. Параллелепипеды и призмы. Пирамиды. Круглые тела.

Цель: изучить основные базовые геометрические понятия, необходимые для осуществления профессиональной деятельности. http://www.mathprofi.ru/skaljarnoe_proizvedenie_vektorov.html

Алгебра и начала анализа:учеб. Для 10-11 кл общеобразоват.учреждений. / А.Н. Колмогоров и др.; под ред. А.Н. Колмогорова.–М.:Просвещение,2003. – 384 с.

Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:

45

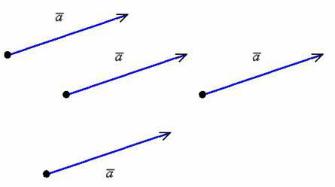
В данном случае началом отрезка является точка , концом отрезка – точка . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи. Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.

!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: , но допустима и запись , которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе. В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: , подразумевая тем самым, что это вектор.

То была стилистика, а сейчас о способах записи векторов:

1) Векторы можно записать двумя большими латинскими буквами:

и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

2) Векторы также записывают маленькими латинскими буквами:

В частности, наш вектор можно для краткости переобозначить маленькой латинской буквой .

Длиной или модулем ненулевого вектора называется длина отрезка . Длина нулевого вектора равна нулю. Логично.

Длина вектора обозначается знаком модуля: , Как находить длину вектора мы узнаем (или повторим, для кого как) чуть

позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки:

46

Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте вектор произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё математически корректно – вектор можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)

Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения вектора имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия.

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.

Действия с векторами. Коллинеарность векторов В школьном курсе геометрии рассматривается ряд действий и правил с

векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников Рассмотрим два произвольных ненулевых вектора и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :

47

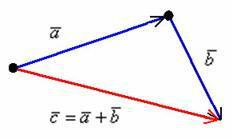
Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего пути с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число Сначала о коллинеарности векторов. Два вектора называются

коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком

противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка: Разбираемся более детально:

48

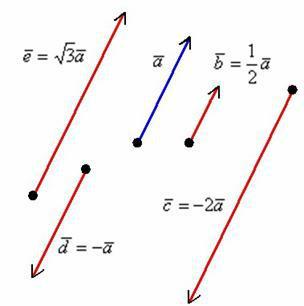
1)Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.

2)Длина. Если множитель заключен в пределах или , то длина вектора уменьшается. Так, длина вектора в два раза меньше длины вектора . Если множитель по модулю больше единицы, то длина вектора увеличивается в раз.

3)Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, . Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4)Векторы сонаправлены. Векторы и также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Координаты вектора на плоскости и в пространстве

49

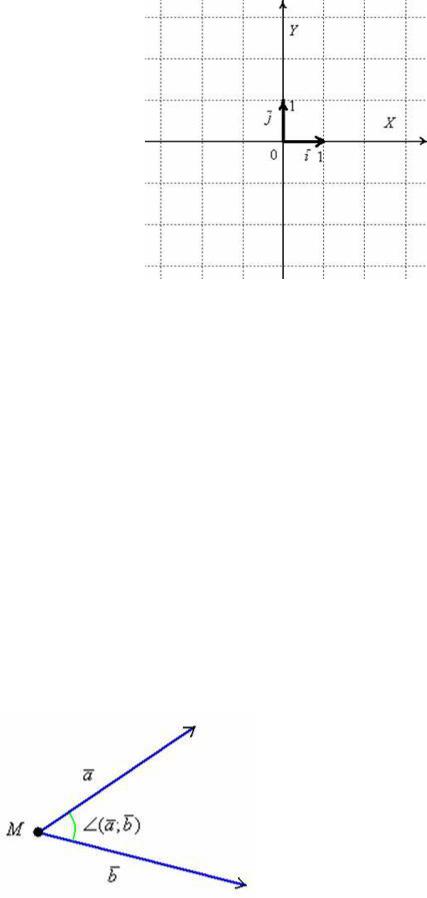
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим

Рекомендую потихоньку привыкать к терминам: вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.

Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: .

Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.

Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.

Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: . Координатные векторы нельзя переставлять местами.

Понятие скалярного произведения

50