из электронной библиотеки / 364183257333934.pdf

Пусть A – множество студентов исторического факультета, B – множество студентов второго курса. Тогда, A ∩ B – множество студентов второго курса, учащихся на историческом факультете.

Подумай! A ∩ U = A, A ∩ A = A

Объединением A и B называется множество C, состоящее из всех элементов A и всех элементов B.

Обозначение: C = A B. Знак называется знаком объединения множеств.

Разностью A и B называется множество C,

U состоящее из всех элементов, принадлежащих множеству А и не принадлежащих множеству B.

Обозначение: C = A \ B

Разность между универсальным множеством и множеством A называется дополнением к

множеству A. Обозначение: Ā=U \ A.

Следовательно, A ∩ Ā = Ø; A Ā = U. Задача.

Разбиение множества на классы. Классификация

В процессе изучения предметов и явлений окружающего мира мы постоянно сталкиваемся с классификацией. Классификация широко используется в биологии, химии, математике, языке и многих других науках. Она облегчает процесс усвоения знаний.

Классификация в любой области человеческой деятельности связана с разбиением множества на подмножества (классы). Например, классификация частей речи, членов предложения, чисел, геометрических фигур и так далее.

Полученные подмножества должны обладать некоторыми свойствами:

1)они не должны быть пустыми;

2)не должны содержать общих элементов;

3)объединение всех подмножеств должно равняться самому множеству.

31

Определение: Классификацией или разбиением множества на классы называется представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств.

Для примера рассмотрим классификацию с помощью двух свойств.

Пусть U – множество студентов института, свойство α - «быть отличником», свойство β - «быть спортсменом». С помощью указанных свойств можно выделить следующие подмножества:

А– множество отличников;

–множество не отличников; В – множество спортсменов;

–множество не спортсменов.

Множество U в этом случае оказывается разбитым на следующие четыре класса (подмножества):

I – множество отличников-спортсменов;

II – множество отличников - не спортсменов;

III – множество не отличников - спортсменов; IV – множество не отличников - не спортсменов;

Можно доказать, что если n – число свойств, то максимальное число классов в разбиении равно 2n.

Число элементов объединения и разности двух конечных множеств

Пусть A и B – конечные множества. Число элементов множества A условимся обозначать символом m(A) и называть численностью множества A.

Определим численность объединения множеств A и B.

Если множества A и B не пересекаются, то m(A B) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.

Если множества A и B пересекаются, то в сумме m(A) + m(B) число элементов пересечения A B содержится дважды: один раз в m(A),а другой – в m(B). Поэтому, чтобы найти численность объединения m(A B) , нужно из указанной суммы вычесть m(A B). Таким образом:

m(A B) = m(A) + m(B) - m(A B)

Определим теперь численность разности множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и

поэтому m(A\B) = m(A).

Если множества A и B пересекаются (см. рис. 1б), то m(A\B) = m(A) - m(A B).

Если В А (см. рис. 1в), то A B = B, и, следовательно, m(A\B) = m(A) -

m(B).

Задания к практической работе «множества и операции над ними»

1.Запишите множество четных и нечетных чисел с помощью характеристического свойства.

2.Приведите пример пустого множества на множестве студентов.

3.Назовите несколько элементов из разностей Z \ N, Q \ R.

32

4.3. Пусть U={1,2,…9}, A = {1,2,3,4,5}. Найти X, если известно, что

a.X \ A = {6,7}, A ∩ X={1,3,5};

b.A X = {1,2,3,4,5,6,7,8}, A \ X = {1,4,5};

c.A X = {1,2,3,4,5,6,7}, A∩X= {1,2}.

5.В группе из 100 туристов 70 человек знают английский язык, 45 знают французский язык и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?

6.Из 40 студенток 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько студенток умеют плавать и играть в шахматы?

7.20 мальчиков поехали на пикник. При этом 5 из них обгорели, 8 были сильно покусаны комарами, а 10 остались всем довольны. Сколько обгоревших мальчиков не было покусано комарами? Сколько покусанных комарами мальчиков также и обгорели? (Сформулируйте эту задачу как лингвистическую, например: анализ наличия 2 предлогов в предложениях; и в общем виде, используя понятия: множество, подмножества и их элементы)

8.В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет, В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?

9.Пусть R – множество букв современного русского алфавита,

A – подмножество R, состоящее из букв, составляющих слово аксиома, B – подмножество R, состоящее из букв, составляющих слово скорость, C – подмножество R, состоящее из букв, составляющих слово паспорт.

10.Задать способом перечисления следующие множества и найти количество их элементов:

а) A B б) B C в) C \ A г) A B C

11.Исследуется текст из 100 предложений. В каждом из 100 предложений имеется либо местоимение «я», либо местоимение «ты», либо оба местоимения. Всего в тексте встретилось 60 местоимений «я» и 50 местоимений «ты». Сколько предложений содержат и местоимение «я» и местоимение «ты»? Сколько предложений содержат местоимение «я» и не содержат местоимения «ты»?

12. Из 35 сотрудников фирмы «Толмач», каждый из которых владеет хотя бы одним иностранным языком, 25 человек знают английский язык, 15 человек – греческий язык, 20 человек – французский язык, 15 человек знают английский и французский языки, 6 – греческий и французский языки и 10 – греческий и английский языки. Сколько сотрудников фирмы знают:

а) все 3 языка?

б) только греческий и французский языки (т.е. знают греческий и французский языки, но не знают английского языка)?

33

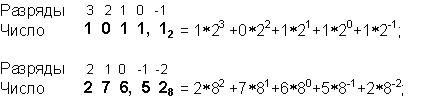
Задания для самостоятельной работы: подготовить сообщения по темам:

Георг Кантор – основатель теории множеств

Системы счисления. Представление чисел в позиционных системах счисления. Машинные системы счисления

Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).

Существуют позиционные и непозиционные системы счисления.

Внепозиционных системах вес цифры (т.е. тот вклад, который она вносит

взначение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

Впозиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

an-1 q n-1 + a n-2 q n-2+ ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,

где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

двоичная (используются цифры 0, 1); восьмеричная (используются цифры 0, 1, ..., 7);

34

шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

представление информации посредством только двух состояний надежно и помехоустойчиво;

возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов,

необходимых для записи чисел.

Двоичная система, удобная для компьютеров, для человека неудобна изза ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2).

Алфавит и арифметика в двоичной системе счисления Алфавит и арифметика в восьмеричной системе счисления

Алфавит и арифметика в шестнадцатеричной системе счисления Алгоритмы перевода чисел из десятичной СС в машинные ( 2 алгоритма) Алгоритмы перевода чисел из машинных СС в десятичную.

Практическая работа

Цель: отработка умений производить арифметические операции в машинных системах счисления. перевода чисел в различных системах счисления

Вычислить: (задания по карточкам)

E2D816+2CA316 EA3516-FC816

35

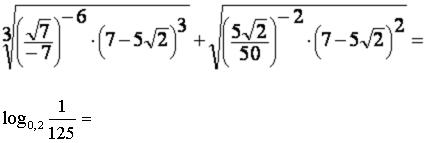
B00216-FFF16

71358+4538

30058-3478

Перевести числа из двоичной СС в восьмеричную и шестнадцатеричную:

100010100,010112

101110110001,1110112

Перевести в двоичную СС:

465,238

714,38 DEF0116

F2,A16

Практическая работа

Цель: отработка алгоритмов перевода чисел в различных системах счисления

Даны 2 слагаемых в десятичной СС 156 и 67. Перевести слагаемые в машинные СС, произвести сложение, результат вернуть в десятичную СС.

Раздел 3. Алгебра

Практическая работа. Корни и степени. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем . Свойства степени с действительным показателем. Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.

Повторение теории.

Вычислить: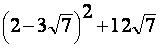

log9243 = 2log63+log64 = log28+log48 =

36

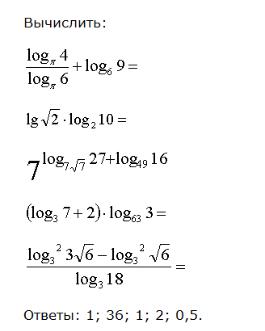
Практическая работа. Алгебраические выражения. Тождественные преобразования.

Уравнения и неравенства. Решение иррациональных, логарифмических и тригонометрических уравнений и неравенств.

Цель занятий: Освоить методы тождественного преобразования алгебраических выражений, методы решения уравнений и неравенств, метод интервалов, решение иррациональных, логарифмических и тригонометрических уравнений и неравенств, систем алгебраических уравнений и неравенств.

Алгебраические выражения. Тождественные преобразования математических выражений.

Теория: Существуют два основных вида математических выражений. Числовые выражения и алгебраические выражения.

Математическое выражение, составленное из чисел, скобок и знаков арифметических действий называется числовым выражением. 7-3 - числовое выражение. (8+3,2)•5,4 - тоже числовое выражение. Обычное число, дробь, любой пример на вычисление без иксов и прочих букв - всё это числовые выражения.

Главный признак числового выражения - в нём нет букв. Никаких. Только числа и математические значки (если надо). И что можно делать с числовыми выражениями? Числовые выражения, как правило, можно считать. Для этого приходится, бывает, раскрывать скобки, менять знаки, сокращать, менять местами слагаемые - т.е. делать преобразования выражений.

Если в числовом выражении появляются буквы - это выражение становится... Выражение становится... Да! Оно становится алгебраическим выражением. Например:

5а2; 3x-2y; 3(z-2); 3,4m/n; x2+4x-4; (а+b)2; ...

и так далее, до бесконечности...)

37

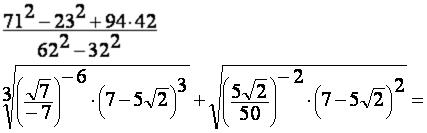
Ещё такие выражения называют буквенными выражениями. Или выражениями с переменными. Это, практически, одно и то же. Выражение 5а +с, к примеру - и буквенное, и алгебраическое, и выражение с переменными.

Понятие алгебраическое выражение - более широкое, чем числовое. Оно включает в себя и все числовые выражения.

(2+3) : (16 - 2•8)

Однако, это выражение тоже не имеет смысла! По той простой причине, что во вторых скобочках - если посчитать - получается ноль. А на ноль делить нельзя! Это запретная операция в математике. Стало быть, с этим выражением тоже ничего делать не надо. При любом задании с таким выражением, ответ будет всегда один: «Выражение не имеет смысла!»

Когда алгебраическое выражение не имеет смысла?

Весь набор чисел, которые можно подставлять в заданное выражение, называется областью допустимых значений этого выражения. Смотрим на выражение с переменными, да соображаем: при каком значении переменной получается запретная операция (деление на ноль)?

А потом обязательно смотрим на вопрос задания. Чего спрашивают-то? Если спрашивают, при каком значении переменной выражение не имеет

смысла, наше запретное значение и будет ответом.

Если спрашивают, при каком значении переменной выражение имеет смысл (почувствуйте разницу!), ответом будут все остальные числа, кроме запретного.

что такое преобразование выражений. Это любое действие с выражением. Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто. Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назватьглавным правилом всей математики. Преобразования, не меняющие

сути выраженияназываются тождественными. Основные способы разложения на множители. Вот они, самые популярные способы:

1.Вынесение общего множителя за скобки.

2.Группировка.

3.Формулы сокращённого умножения.

4.Разложение квадратного трёхчлена. Вычислить:

38

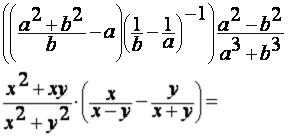
Упростить:

Практические советы:

1.Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!

2.Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах - считаем.

3.Если второй совет не сработал, пробуем применить замену переменной.

Витоге может получиться уравнение, которое легко решается. Чаще всего - квадратное. Или дробное, которое тоже сводится к квадратному.

4.Для успешного решения показательных уравнений надо степени

некоторых чисел знать «в лицо». 22х – 8 х+1 = 0 (х=-3)

3 2х+4 -11·9х = 210 при решении показательных уравнений очень часто помогает вынесение общего множителя за скобки

32х(34 - 11) = 210 ч=0,5

Замена переменной в решении показательных уравнений. Примеры.

4х - 3·2х +2 = 0

2х = t

Тогда 22х = 2х2 = (2х)2 = t2 х1=0, х2=1

Решить уравнения:

6х = 216

8 х+1 = 0,125

Посложнее:

2 х+3 – 2 х+2 - 2х = 48

9х - 8·3х = 9

2х – 2 0,5х+1 - 8 = 0

39

Неравенства – запись вида f(x)*g(x), где * знаки отношений . Неравенства со знаком > или < называется строгим; ≥, ≤ - нестрогим.

Решение неравенства - число, обращающее неравенство в верное числовое неравенство. Множество решений часто бывает набором промежутков. Ответ можно записать как в виде промежутков, так и изобразить его.

Свойства неравенств:

1)переносить из одной части неравенства в другую число или переменную: перенесем число 3 в правую часть неравенства х – 3 > 2, получим х > 5; перенесем 2х в левую часть неравенства 3х < 2х + 7, получим х < 7.

2)умножить (делить) обе части неравенства на положительное число, не меняя знак, либо на отрицательное число, изменив знак неравенства: разделим на 2

–многочлены) применяется метод интервалов.

Чтобы решить неравенство (например, х2 + х > 6) методом интервалов, надо:

1.перенести все слагаемые в левую часть так, чтобы правая часть оказалась равной нулю (получим: х2 + х – 6 > 0);

2.найти область определения функции, стоящей в левой части (для функции: х2 + х – 6, х – любое число);

3.приравнять левую часть к нулю и решить полученное уравнение (х2 + х –

6= 0, D = 25, x1 = 2, x2 = -3);

4.отметить на числовой прямой область определения и полученные решения уравнения, в результате прямая разобьется на некоторое число промежутков (на 3):

5.в каждом из получившихся промежутков выбрать по точке (возьмем в первом промежутке –4, во втором 0, в третьем 3);

6.вычислить значение функции, стоящей в левой части неравенства пункта 1) (х2 + х – 6 > 0), в каждой из выбранных точек (в точке х = -4, х2 + х – 6 = 6, в точке х = 0 х2 + х – 6 = 6);

7.над каждым из промежутков на числовой прямой поставить знак «+», если вычисленное значение в соответствующей точке положительно, и знак « - « – если отрицательно (в первом и третьем промежутке получились положительные значения, во втором – отрицательное);

8.в ответе записать промежутки, знак которых совпадает со знаком неравенства (( - ; -3) или (2; + ∞ )).

Все сказанное относится и к квадратным неравенствам. Решить неравенства:

(х-2)(х+7)<0

(x+9)(x-3)(1-x)<0 X(2x+8)(x-3)>0

40