
- •Квадратичные формы
- •Элементы теории множеств
- •3. Аксиома сложения и умножения.
- •4. Аксиомы порядка.
- •5. Аксиомы порядка, связанные с операциями.
- •6. Аксиома непрерывности.
- •Функции действительных переменных
- •Способы задания функции одной переменной
- •Функции на множестве натуральных чисел в комбинаторике
- •Последовательности
- •Предел числовой последовательности
- •Предел функции. Свойства пределов
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов функций
- •Второй замечательный предел и его следствия
Бесконечно малые и бесконечно большие функции
Определение 1.
Функция
![]() называется бесконечно малой функцией
(бесконечно малой) при
называется бесконечно малой функцией
(бесконечно малой) при![]() ,
если
,
если![]() .
.
Определение 2.
Функция
![]() называется бесконечно большой функцией
(бесконечно большой) при
называется бесконечно большой функцией
(бесконечно большой) при![]() ,
если
,
если![]() .
.
Следствие.
Функция
![]() при
при![]() бесконечно малая, а
бесконечно малая, а![]() - бесконечно большая.
- бесконечно большая.
Определение 3.
Функции
![]() и
и![]() называется бесконечно малыми одного
порядка малости при
называется бесконечно малыми одного
порядка малости при![]() ,
если
,
если![]() ,
причем
,
причем![]() .
.
Определение 4.
Функции
![]() и
и![]() называется эквивалентными бесконечно
малыми при
называется эквивалентными бесконечно
малыми при![]() ,
если
,
если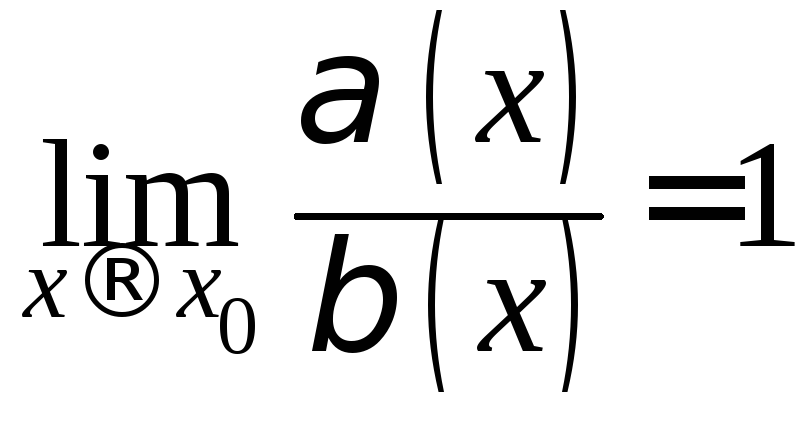 .
.
Определение 5.
Функция
![]() называется бесконечно малой более
высокого порядка малости, чем
называется бесконечно малой более
высокого порядка малости, чем![]() ,
при
,
при![]() ,
если
,
если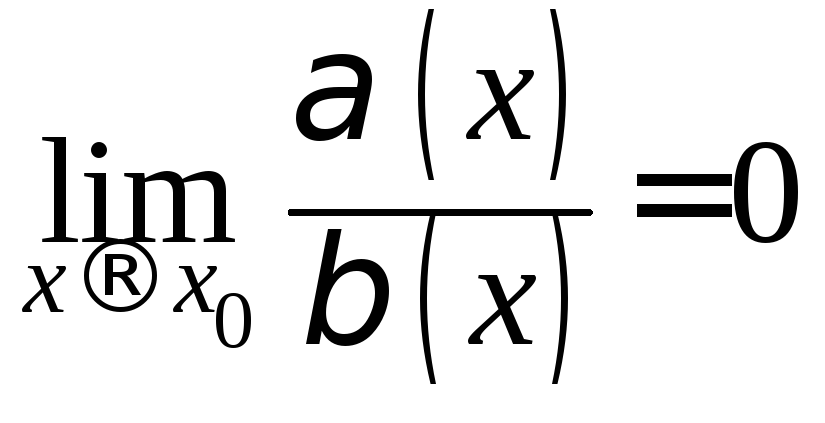 .
.
Известны следующие свойства бесконечно малых.
Сумма конечного числа бесконечно малых – бесконечно малая.
Произведение бесконечно малой и конечной величины – величина бесконечно малая.
Произведение бесконечно малых – бесконечно малая.
Свойства пределов функций
Предел постоянной равен самой постоянной. Это свойство следует из определения предела.
Постоянную можно выносить за знак предела.
![]() .
.
Предел суммы двух функций равен сумме пределов этих функций, если они существуют.
![]() .
.
Предел произведения двух функций равен произведению их пределов, если они существуют.
![]()
Предел отношения двух функций:
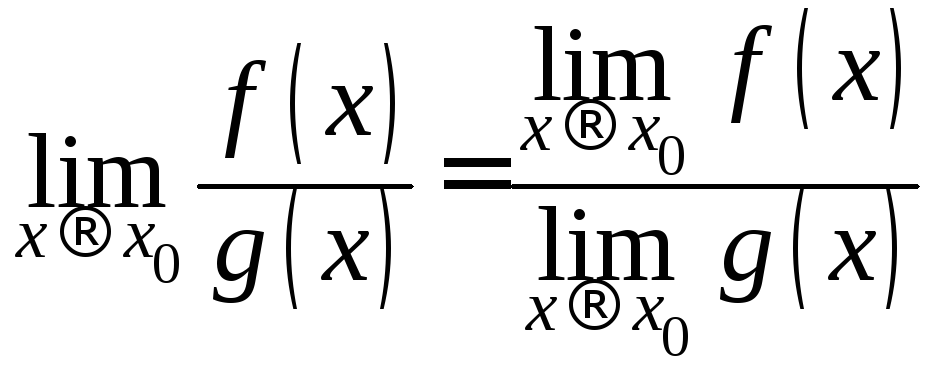 ,если оба
предела существуют и
,если оба
предела существуют и
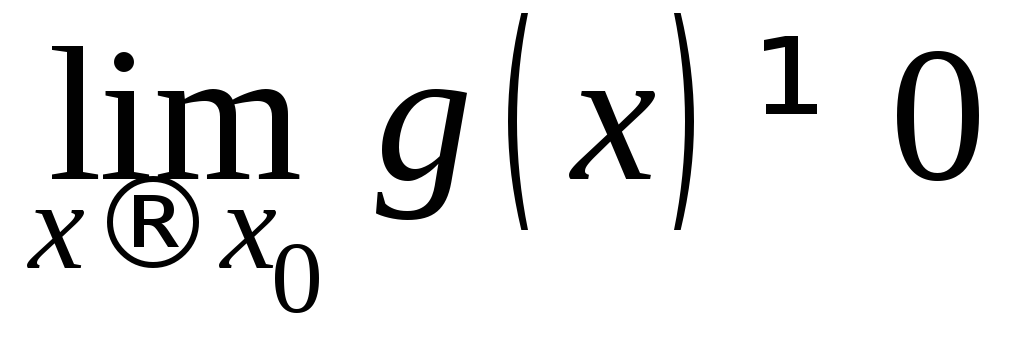 .
.Если
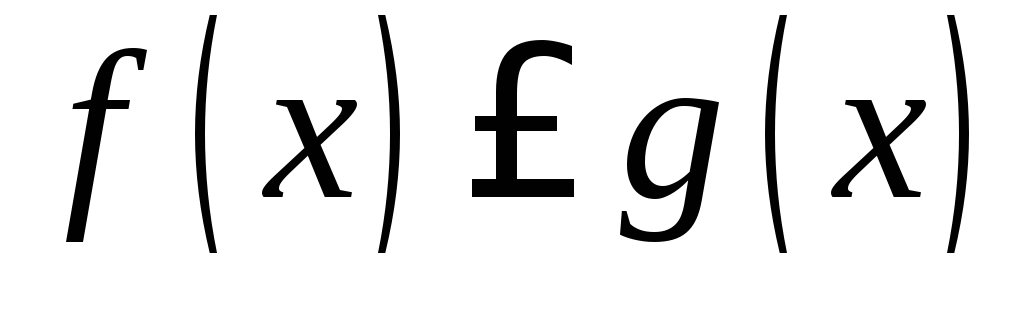 ,то
,то
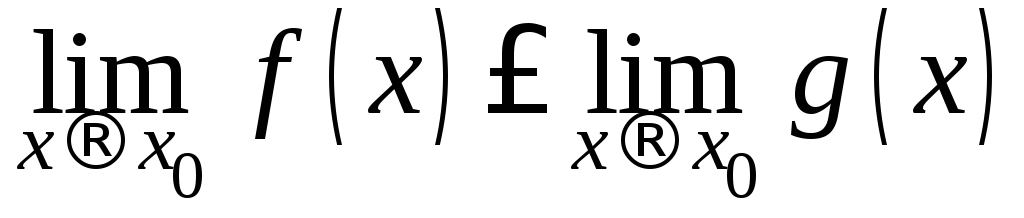 .
.Если
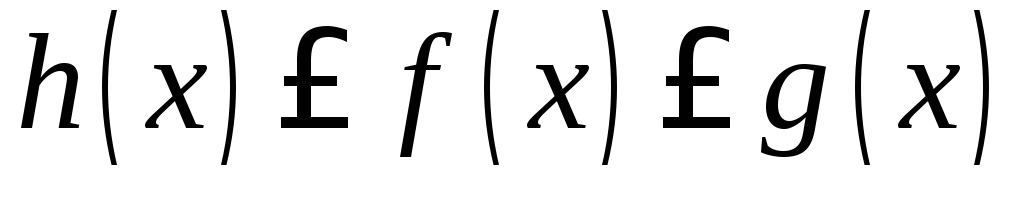 и
и
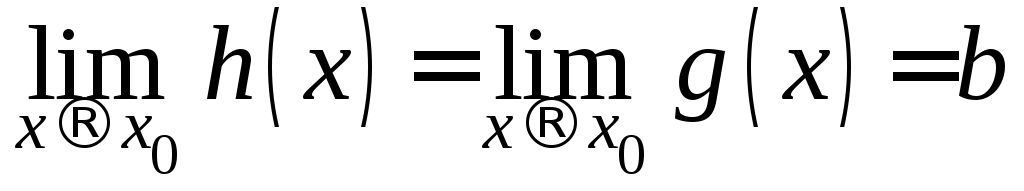 ,то
,то
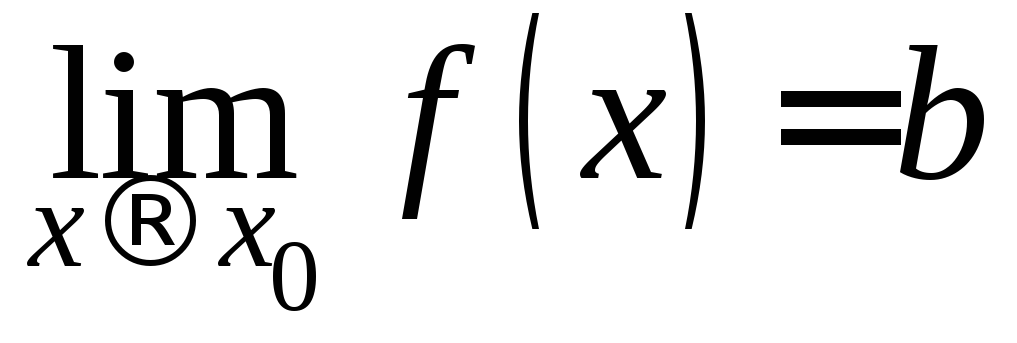 .
(Теорема о
двух полицейских).
.
(Теорема о
двух полицейских).
Первый замечательный предел
Докажем, что справедлива формула:
![]() .
.
Прежде
всего, заметим, что вследствие нечетности
функции
![]() отношение
отношение![]() при
при![]() ,
близком к 0, положительно при любом знаке
,
близком к 0, положительно при любом знаке![]() .
Достаточно предположить, что
.
Достаточно предположить, что![]() приближается к 0, оставаясь положительным.
В противном случае мы сменим знак
приближается к 0, оставаясь положительным.
В противном случае мы сменим знак![]() ,
что не повлияет на результат. Используем
геометрическое доказательство. Рассмотрим
сектор круга радиуса 1 с углом при
вершине, равным
,
что не повлияет на результат. Используем
геометрическое доказательство. Рассмотрим
сектор круга радиуса 1 с углом при
вершине, равным![]() .BM
– дуга граничной окружности сектора,
A
– его вершина, AB
= AM
= 1. BD
– отрезок касательной к дуге BM
в точке B.
BC
– перпендикуляр, опущенный из точки B
на отрезок AM.
.BM
– дуга граничной окружности сектора,
A
– его вершина, AB
= AM
= 1. BD
– отрезок касательной к дуге BM
в точке B.
BC
– перпендикуляр, опущенный из точки B
на отрезок AM.
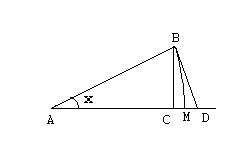
В
силу последовательной вложимости друг
в друга треугольника ABM,
сектора ABM
и треугольника ABD
соответствующие соотношения имеют
место между площадями этих фигур:
![]() .
Имеем
.
Имеем![]() .
Поэтому получаем неравенство
.
Поэтому получаем неравенство![]() .
Если мы поделим все части этого неравенства
на
.
Если мы поделим все части этого неравенства
на![]() ,
то в силу предположения о знаке
,
то в силу предположения о знаке![]() знаки неравенства не изменятся. Поэтому
мы имеем
знаки неравенства не изменятся. Поэтому
мы имеем![]() .
А теперь устремим
.
А теперь устремим![]() к нулю и применим теорему о двух
полицейских. Мы получим
к нулю и применим теорему о двух
полицейских. Мы получим![]() .
Осталось применить свойство 5) пределов
для получения предела обратной величины:
.
Осталось применить свойство 5) пределов
для получения предела обратной величины:![]() .
.
Второй замечательный предел и его следствия
Справедливы следующие формулы, называемые вторым замечательным пределом:
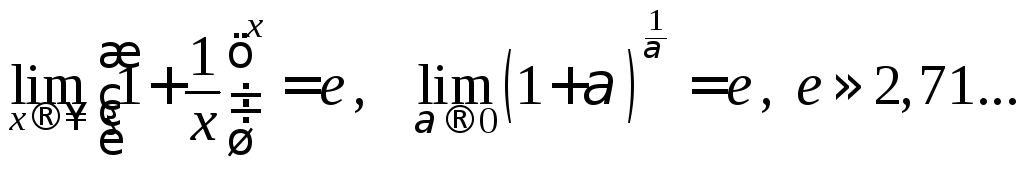
Равносильность
этих формул следует из связи переменных:
![]() .
.
Мы получали число
Непера
![]() из подобной формулы, где была
последовательность, а не функция.
Заметим, что здесь в первой из приведенных
формул переменная
из подобной формулы, где была
последовательность, а не функция.
Заметим, что здесь в первой из приведенных
формул переменная![]() может стремиться как к
может стремиться как к![]() ,
так и к
,
так и к![]() ,
а также может просто расти по абсолютной
величине, меняя знак произвольно.
Приведенная формула имеет следующие
следствия.
,
а также может просто расти по абсолютной
величине, меняя знак произвольно.
Приведенная формула имеет следующие
следствия.
1. Если мы формально прологарифмируем вторую из приведенных формул, мы получим 1-е следствие второго замечательного предела:
![]() .
.
2.
Другим следствие второго замечательного
предела является предел, получаемый из
предыдущего заменой
![]() :
:
![]() .
.
3.
Рассмотрим теперь предел
![]() .
Сделаем замену
.
Сделаем замену
![]() .
При такой замене
.
При такой замене![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
Получим
.
Получим
![]()
