3. Аксиома сложения и умножения.

1) справедливо .

4. Аксиомы порядка.

1) справедливо .

2) таких, что , справедливо одно из двух соотношений: или .

3) Если выполняются одновременно соотношения и , то справедливо соотношение .

4) Если выполняются одновременно соотношения и , то .

5. Аксиомы порядка, связанные с операциями.

1) Если , то для справедливо .

2) Если выполняются одновременно соотношения и , то .

6. Аксиома непрерывности.

Пустьи – подмножества множества , причем для и для справедливо . Тогда такое, что и для и для .

Все перечисленные аксиомы обеспечивают те свойства вещественных чисел, которыми мы привычно пользуемся.

Последняя аксиома кажется лишней в перечне аксиом. Однако именно эта последняя аксиома позволяет ввести иррациональные числа в множество действительных чисел.

Действительно, первые пять аксиом справедливы и для множества рациональных чисел , то есть, чисел, представимых в виде отношения , где – целое число, а – натуральное число. Однако еще древние греки знали, например, что число, квадрат которого равен 2, не является рациональным. Существование иррациональных чисел во множестве R доказывается именно применением аксиомы непрерывности.

Известной еще древним грекам является интерпретация множества в виде бесконечной прямой, на которую нанесена точка (O), являющаяся началом отсчета как в положительном, так и в отрицательном направлениях. Действительные числа – это точки прямой с расстояниями от точки отсчета, равными величинам чисел. Такой интерпретацией мы активно пользуемся со школы, называя положительной бесконечностью () условный предел при удалении точки по прямой вправо и отрицательной бесконечностью () условный предел при удалении точки по прямой влево.

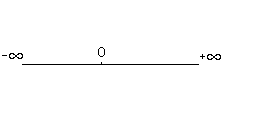
Другой моделью множества является окружность. Характерной особенностью такой интерпретации является то, что аналогом бесконечности является одна из точек окружности. Покажем, что между точками бесконечной прямой и конечной окружности существует взаимнооднозначное соответствие, позволяющее заменять одну модель на другую.

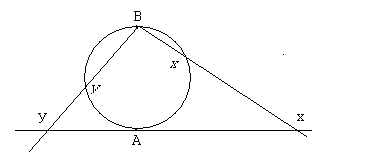
Представим окружность, касающуюся прямой в точку A, которую мы назовем полюсом. Другим полюсом (B) назовем точку, диаметрально противоположную A. Проводя из B лучи, пересекающие окружность и данную прямую, мы получим взаимнооднозначное соответствие точек окружности и прямой. Полюс A будут соответствовать самому себе. Полюс B будет соответствовать бесконечности. При этом понятия и будут означать только направление движения к одной и той же точке B, соответствующей бесконечно удаленной точке.

Функции действительных переменных

Числовые величины могут быть переменными и постоянными, то есть меняющимися или не меняющимися в процессе исследования. Переменные величины могут быть независимыми и зависимыми – меняющимися в зависимости от каких-то других величин.

Эти понятия также условны. Если рассмотреть уравнение окружности , в нем участвует две переменные величины и . Одной из них можно придавать в некоторой области любые значения, другая находится из приведенного уравнения. Следовательно, одну из них можно считать независимой, другую – зависимой переменной. При этом независимой переменной может считаться любая из них, тогда вторая будет зависимой.

Функция – это закон, по которому каждому элементу некоторого множества (область определения) ставится в соответствие элемент другого множества (область значений).