Последовательности

Определение. Функция одного переменного, заданная на множестве N, называется последовательностью. Значение функции при n=1, называется первым членом последовательности (), значение приn=2 – вторым членом последовательности (), ….

Последовательности бывают числовыми, если все ее элементы – числа и функциональными, когда ее элементы – функции.

Примеры. 1.– числовая последовательность,

2. 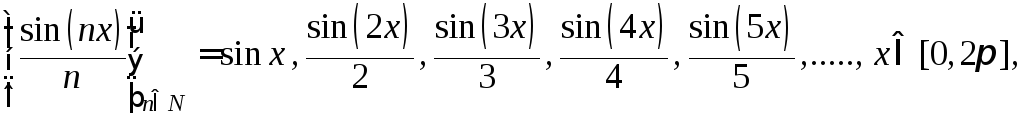– функциональная последовательность.

Предел числовой последовательности

Определение. Число называется пределом числовой последовательности(), если длятакое, что присправедливо неравенство:. Произвольность положительного числаобеспечивает возможность для членов последовательностис большими номерамиподойти сколь угодно близко к пределу.

Последовательность, имеющая конечный предел, называется сходящейся последовательностью. В противном случае последовательность называют расходящейся.

Примеры. 1. Величина может быть сделана сколь угодно малой при достаточно больших значениях. Следовательно,.

2. Величина может быть сделана сколь угодно малой при достаточно больших значениях. Следовательно, .

3. Последовательность возрастает с ростом, стремясь к бесконечности. Конечного предела эта последовательность не имеет. Следовательно, эта последовательность расходится.

4. Последовательность не имеет предела, и значит, расходится.

5. Последовательность

является сходящейся, ее предел называется числом Непера и обозначается буквой , причем

Таким образом, .

Определение. Последовательность называетсябесконечно малой, если ее предел равен нулю, т.е для такое, что присправедливо неравенство:.

Определение. Расходящаяся последовательность называется бесконечно большой, если для такое, что присправедливо неравенство:. Произвольность числапозволяет значениям членов последовательности с большими номерами быть сколь угодно большими по абсолютной величине.

Очевидно, что последовательность является бесконечно малой тогда и только тогда, когда последовательностьявляется бесконечно большой.

Предел функции. Свойства пределов

Если при вычислении предела последовательности всегда , то, вычисляя предел функции, следует оговаривать, к чему стремится ее аргумент. Рассмотрим, в чем различие между пределами последовательностии функции. Если в последовательностивозрастает, принимая только значения из множества натуральных чисел, томожет возрастать, принимая любые вещественные значения. Пределы последовательности и функции в этом случае равны нулю.

В то же время имеет смысл рассмотреть предел . Стоящая под знаком предела функция увеличивается с приближением ее аргументак нулю, оставаясь положительной, причем, присколь угодно близких к нулю, ее значение становится все большим и большим. Ясно, что. Поскольку прирассматриваемая функция не существует, этот ее предел дает важнейшую информацию – показывает поведение функции в окрестности предельной точки. При подходе к этой точке она уходит в бесконечность.

Определение 1. Число называется пределом функциипри, если для любой последовательности значений аргумента, стремящейся к, соответствующая ей функциональная последовательностьсходится к.

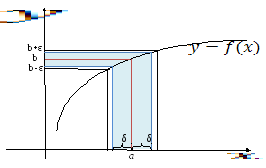
В первой все ее члены больше a, и мы подходим к точке a справа, во второй все элементы меньше предельного значения аргумента, подходим к точке a слева, в третьей элементы последовательности расположены как слева, так и справа от предельного значения a. Соответствующие им функциональные последовательности во всех трех случаях стремятся кb. Если для любой другой последовательности , стремящиеся кa, последовательность также стремится кb, то предел функции равен этому числу, что видно из рисунка.

Приведенное определение предела функции в точке, связанное с рассмотрением числовых последовательностей, неудобно тем, что реально невозможно изучить все числовые последовательности, сходящиеся к числу . Поэтому для исследования существования предела пользуются вторым определением, равносильным первому.

Определение 2. Число называется пределом функциипри, если.

Словесная формулировка приведенной фразы такова: число называется пределом функциипри, если для любого положительногосуществует такое положительное, что для любого, для которого выполняется неравенство, выполняется неравенство.

Определение 2а. Число называется пределом функциипри, если.

Доказана эквивалентность определений 1 и 2, то есть из 1 следует 2, и наоборот.

Определение 3. Число называется левым пределом функциипри(пределом слева), если для любой последовательности значений аргумента, стремящейся кслевасоответствующая ей функциональная последовательностьсходится к. Обозначение.

Определение 4. Число называется правым пределом функциипри(пределом справа), если для любой последовательности значений аргумента, стремящейся ксправасоответствующая ей функциональная последовательностьсходится к. Обозначение.

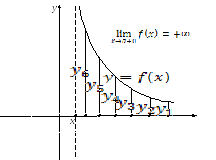
Пример. Вычислим. Поскольку, показатель степени отрицательный, следовательно,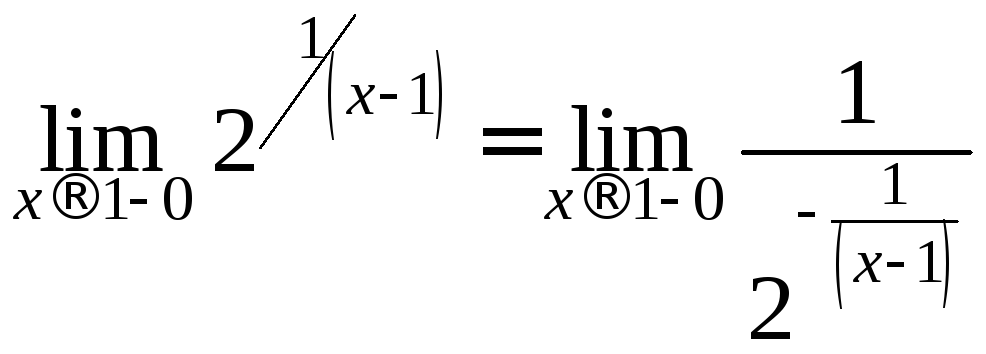. Теперь показатель степени положительный и пристремится к, ясно, что левый предел этой функции приравен нулю. В то же время правый предел, так как показатель степени положителен и стремится к.

Очевидно, не существует, так как при подходе к предельному значению аргумента слева и справа получаем разные значения, и определение 1 не выполняется.