
- •11. Дифференциальные уравнения
- •11.1. Дифференциальные уравнения первого порядка.
- •Рис 11.1
- •Рис 11.2
- •11.2 Дифференциальные уравнения с разделяющимися переменными
- •Упражнения
- •Упражнения
- •11.4 Линейные ду первого порядка.
- •11.5 Уравнение Бернулли
- •Упражнения
- •11.6 Дифференциальные уравнения второго порядка.
- •11.7. Ду второго порядка, допускающее понижение порядка
- •Упражнения
- •11.8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лоду)
- •Упражнения
- •11.9. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лнду).
- •Упражнения
Упражнения
Найти общие решения и частные, удовлетворяющие начальным условиям:
11.44.
![]() – 7
– 7![]() +
12y
= 0;
+
12y
= 0;
11.45.
![]() + 2
+ 2![]() +y
= 0;
+y
= 0;
11.46.
![]() +
+![]() +
2y
= 0;
+
2y
= 0;
11.47.
![]() + 2
+ 2![]() +
3y
= 0;
+
3y
= 0;
11.48.
![]() –
3
–
3![]() +
2y
= 0, y=3,
+
2y
= 0, y=3,
![]() = 4 при 0;
= 4 при 0;
11.49.
![]() – 2
– 2![]() +y
= 0, y=1,
+y
= 0, y=1,
![]() = 0 при 0;
= 0 при 0;
11.9. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лнду).
Линейное неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид:
![]() (11.65)
(11.65)
где p
и q
-действительные числа, f(x)
![]() 0
– некоторая функция.
0
– некоторая функция.
Интегрирование.
1 способ. Метод вариации произвольных постоянных.
Находим сначала общее решение, соответствующее (11.65) ЛОДУ (11.53):
y = C1y1 + C2y2. (11.66)
Общее решение ЛНДУ (11.65) находим в виде (11.66), полагая C1 =C1(x); C2 = C2(x), то есть:
y = C1(x) y1(x) + C2(x)y2(x) (11.67)
Неизвестные функции C1(x) и C2(x) находятся из системы:
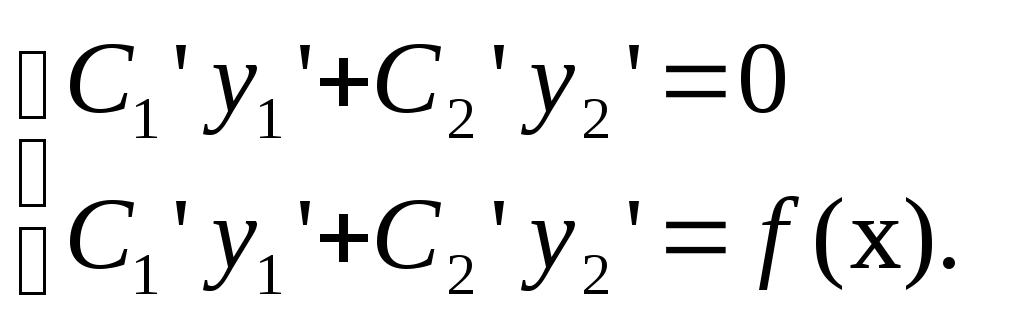 (11.68)
(11.68)
Примеры
11.50. Найти общее решение ЛНДУ(11.69)
![]() –3
–3![]() +
2y
=
+
2y
=
![]() .
(11.69)
.
(11.69)
Решение. Рассмотрим ЛОДУ, соответствующее ЛНДУ(11.69)
![]() –3
–3![]() +
2y
= 0. (11.70)
+
2y
= 0. (11.70)
Характеристическое уравнение:
λ² - 3λ + 2 = 0.
Дискриминант:
D=3²
- 4![]() 2
=1>0. Корни характеристического уравнения
λ1=
1; λ2
= 2.
2
=1>0. Корни характеристического уравнения
λ1=
1; λ2
= 2.
Частные решения:
y1(x)
=
![]() иy2(x)
=
иy2(x)
=
![]()
Общее решение:
y
= C1![]() +C2
+C2![]() .
(11.71)
.
(11.71)
Общее решение ЛНДУ (11.69) находим в виде (11.711), но полагаем C1 =C1(x); C2 = C2(x), то есть
y
= C1(x)
![]() +C2(x)
+C2(x)
![]() .
(11.72)
.
(11.72)
Неизвестные функции C1(x) и C2(x) определяем из системы:
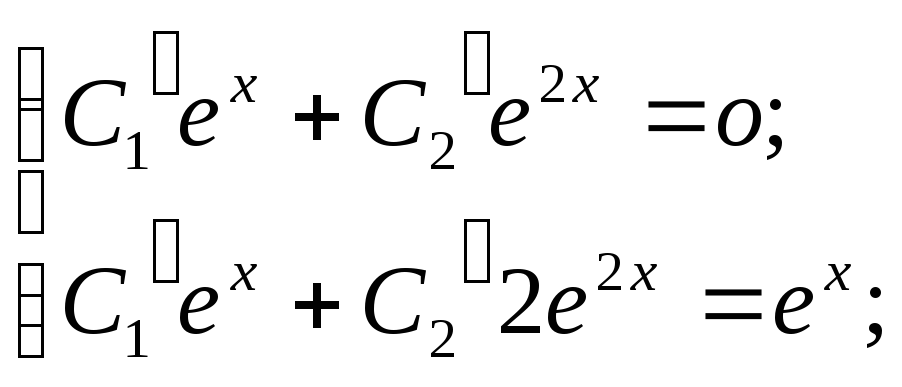
откуда C1’=
-1, C2’
=
![]() .
Интегрируем полученные ДУ относительно
неизвестных функцияхC1(x)
и C2(x),
получаем:
.
Интегрируем полученные ДУ относительно
неизвестных функцияхC1(x)
и C2(x),
получаем:
C1
= - х + C3;
C2
= -
![]() +C4,
(11.73)
+C4,
(11.73)
где C3 и C4 - произвольные постоянные.
Подставляем (11.73) в (11.72):
y=(-х
+ C3)
![]() +
(-
+
(-![]() +C4)
+C4)
![]() ,
или
,
или
y=
C3
![]() +C4
+C4
![]() + (-x
-1)
+ (-x
-1)
![]() - общее решение ЛНДУ (11.69).
- общее решение ЛНДУ (11.69).
11.51. Найти общее решение ЛНДУ:
![]() –2
–2![]() +y
= x
+y
= x![]() .
(11.74)
.
(11.74)
Решение. Рассмотрим ЛОДУ, соответствующее ЛНДУ (2.34):
![]() –2
–2![]() +y
= 0.
(11.75)
+y
= 0.
(11.75)
Характеристическое уравнение:
λ² - 2λ + 1 = 0.
Дискриминант D=0. Корни: λ1= λ2=1.
Частные решения:
y1
=
![]() ;y2
= x
;y2
= x![]() .
.
Общее решение ЛОДУ (2.35):
y=(C1+
xC2)![]() .
(11.76)
.
(11.76)
Общее решение ЛНДУ (11.74) находим в виде (11.76), но полагаем C1 =C1(x); C2 = C2(x), то есть:
y
= (C1(x)
![]() +xC2(x))
+xC2(x))![]() .
(11.77)
.
(11.77)
Неизвестные функции C1(x) и C2(x) находим из системы:

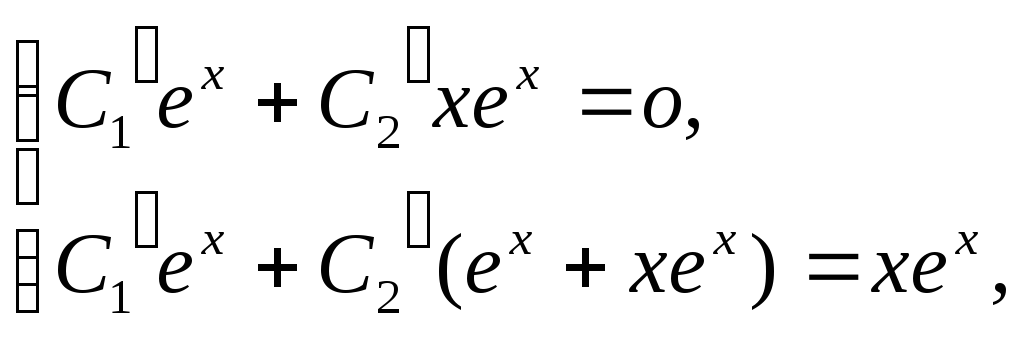
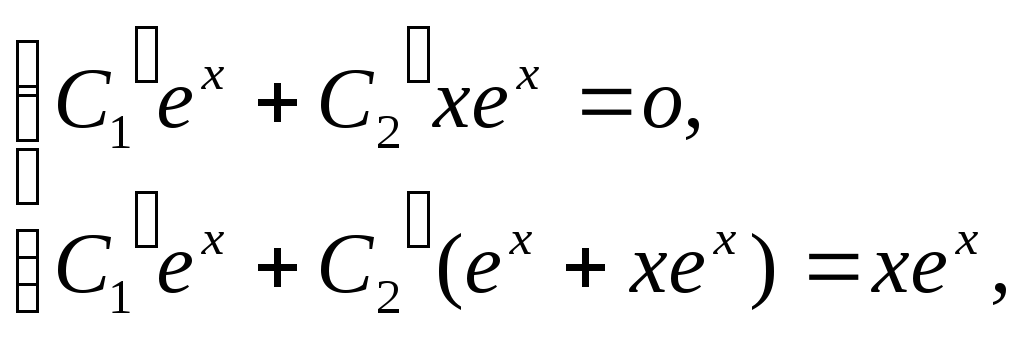
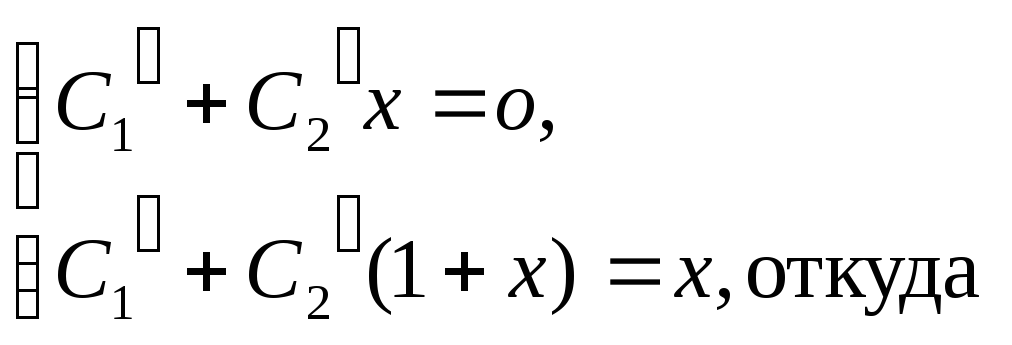
C1(x)=
-
![]() +C3;
C2(x)
=
+C3;
C2(x)
=
![]() + C4,
(11.78)
+ C4,
(11.78)
Функции (11.78) подставим в (11.77):
y=((![]() + C4)x
+ (-
+ C4)x
+ (-
![]() +C3))
+C3))![]() ,
или
,
или
y=
![]() - (11.79)
- (11.79)
общее решение ЛНДУ (2.34).
способ.
Структура общего решения ЛНДУ (11.65):
y = y0 + Y, (11.80)
где Y – общее решение соответствующего (11.65) ЛОДУ (11.53), y0 – частное решение (11.65), зависящее от вида функции f(x).
Частное решение y0 находим по виду правой части (11.65) методом неопределенных коэффициентов:
f(x) =
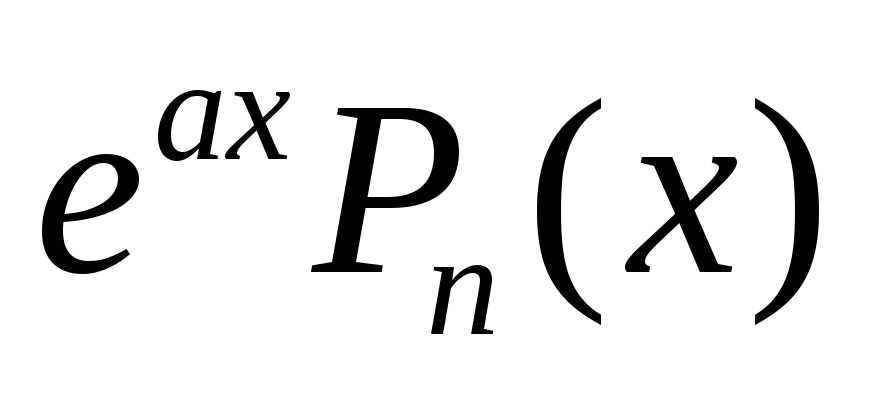 ,
где
,
где 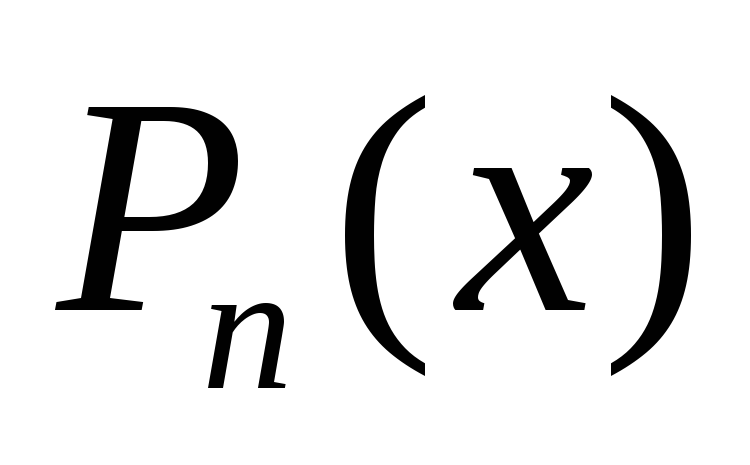 -многочленстепени n;
-многочленстепени n;
если a не является корнем характеристического уравнения, то y₀=
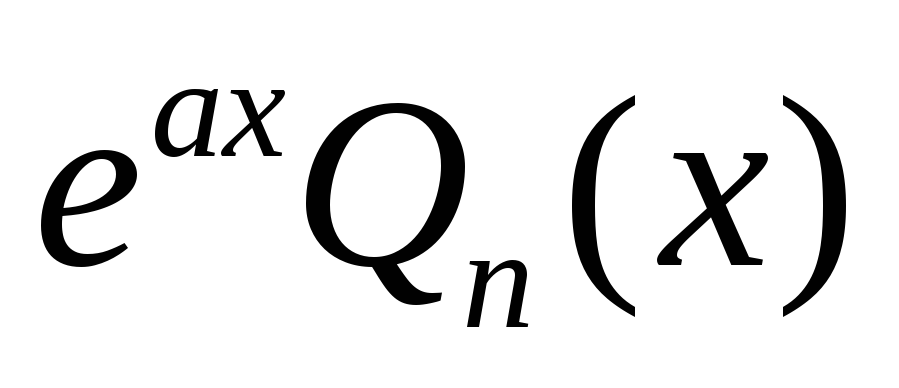 ,
где
,
где 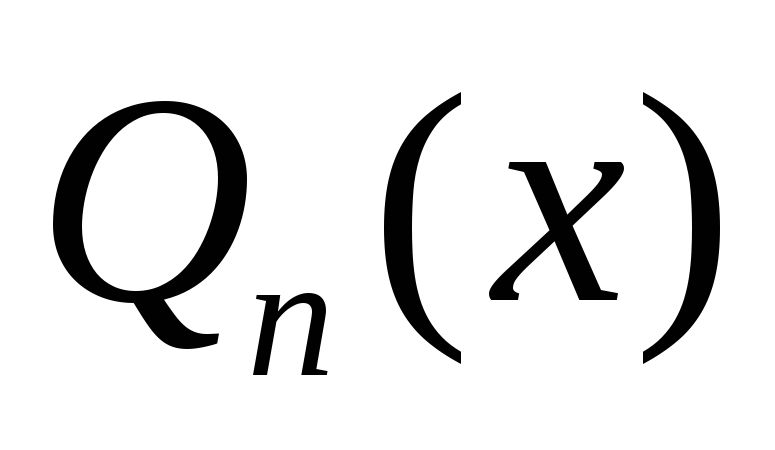 -многочлен степени
n
c
неопределенными коэффициентами;
-многочлен степени
n
c
неопределенными коэффициентами;если a – корень характеристического уравнения, кратности r (r =1 или r=2), то y₀=
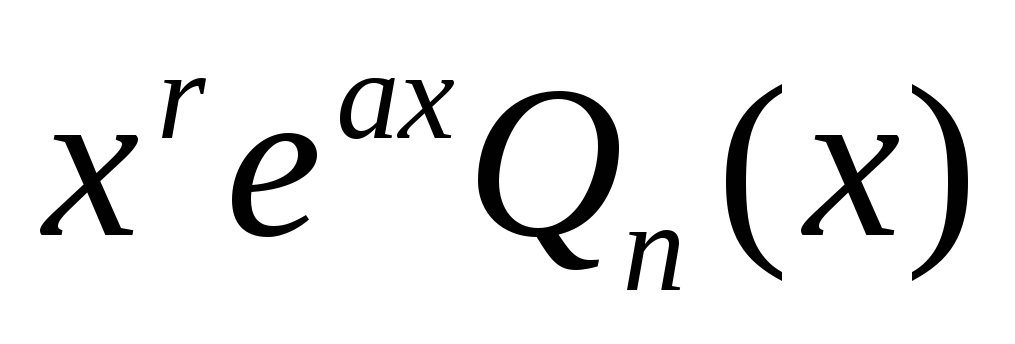 ;
;
f(x) =
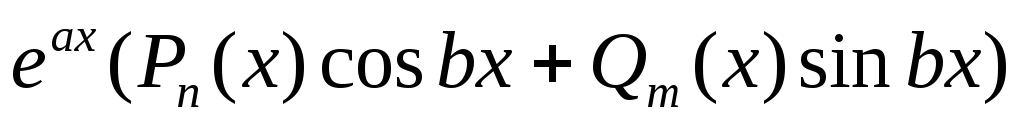 ,
,
если
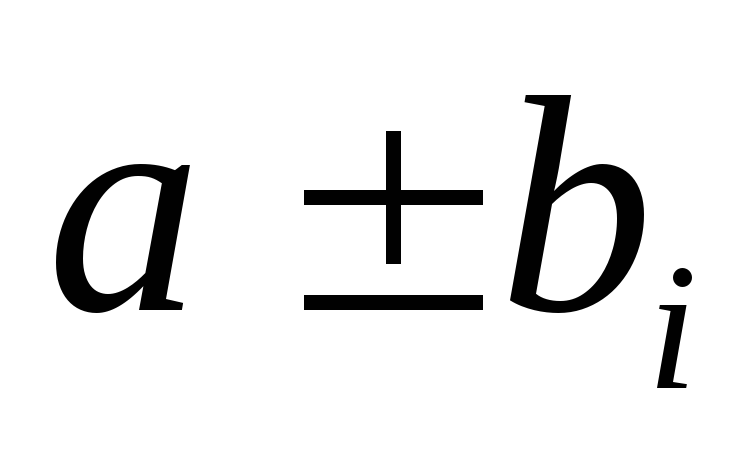 не является корнем характеристического
уравнения, тоy₀=
не является корнем характеристического
уравнения, тоy₀=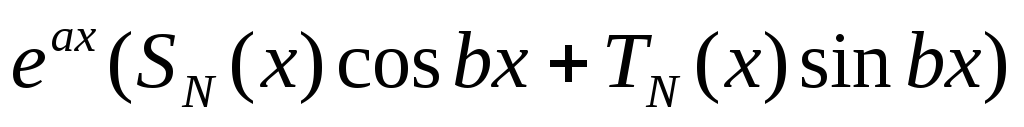 ,
где
,
где 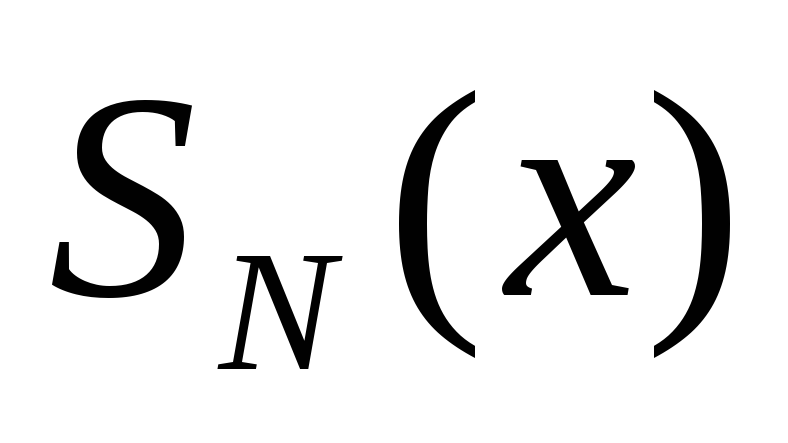 и
и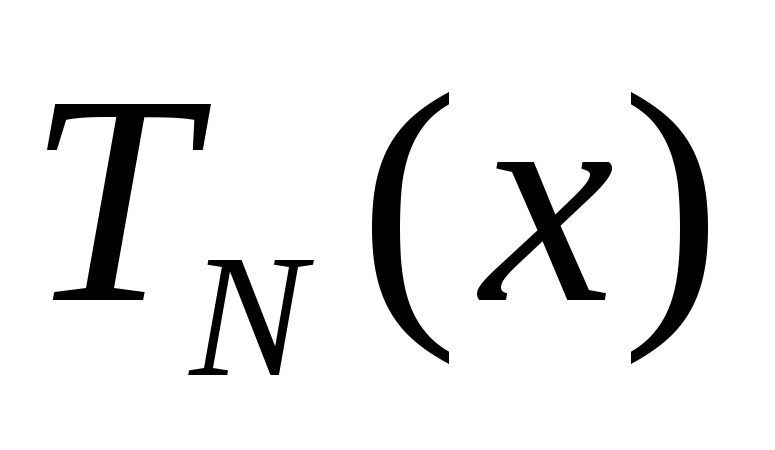 -многочлены
степени N=max
-многочлены
степени N=max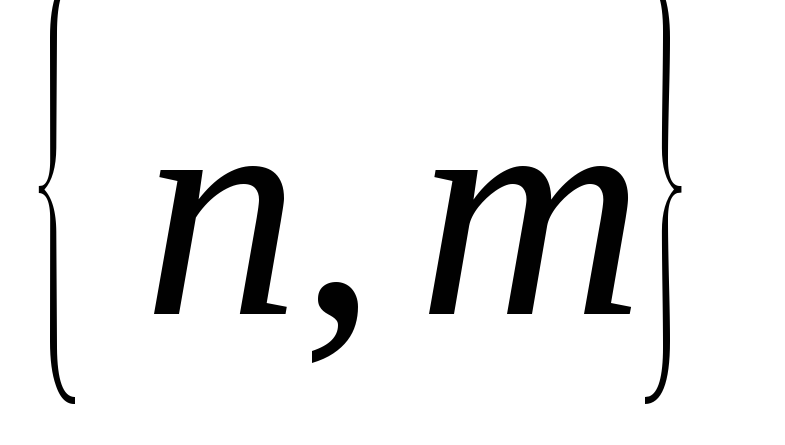 с неопределенными коэффициентами,
с неопределенными коэффициентами,
если
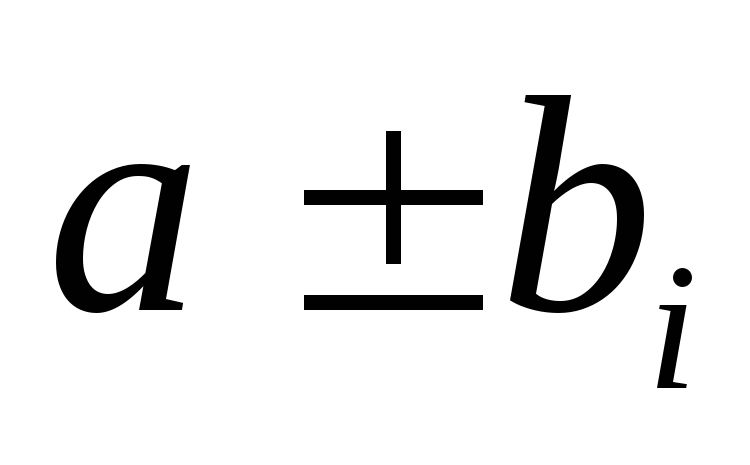 - корни характеристического уравнения,
то
- корни характеристического уравнения,
то
y₀=![]() ,
,
f(x) = f₁(x) + f₂(x) + …+ fk(x),
 - частные решения уравнений
- частные решения уравнений
 +p
+p +
qy
=
+
qy
=
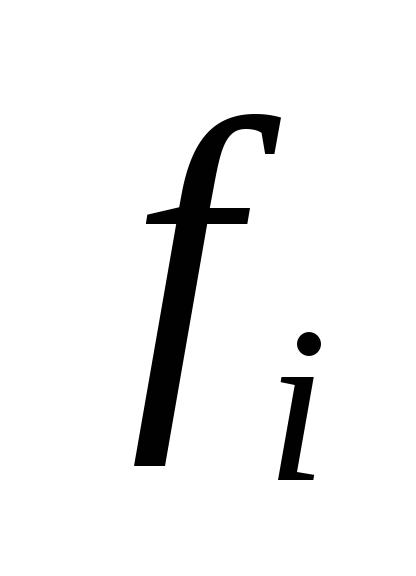 (x),тогда
(x),тогда
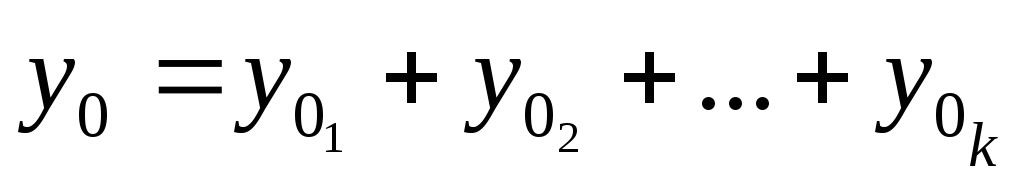 - решение ЛНДУ с правой частью
- решение ЛНДУ с правой частью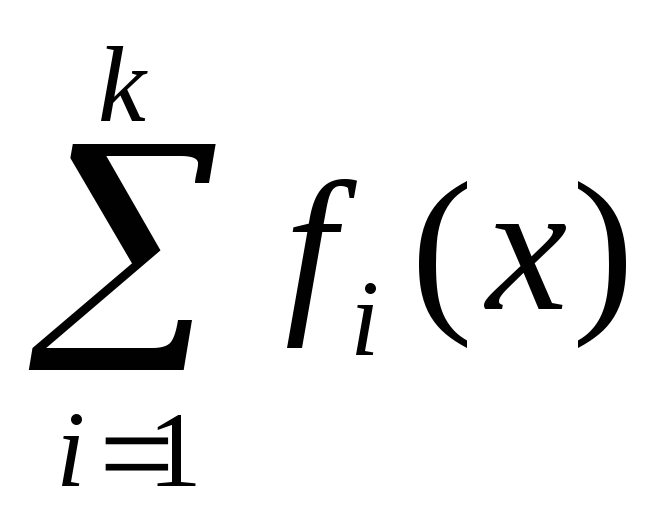 .
.
Примеры
11.52. Найти общее решение ЛНДУ:
![]() - 2
- 2![]() +y
=x
+y
=x![]() (11.81)
(11.81)
Решение Общее решение ЛНДУ (11.81) находим в виде:
y
= ![]() +Y,(11.82)
+Y,(11.82)
где ![]() -частное решение
(11.81), Y
- общее решение ЛОДУ
-частное решение
(11.81), Y
- общее решение ЛОДУ
![]() - 2
- 2![]() +y
= 0.
(11.83)
+y
= 0.
(11.83)
Имеем:
Y
=(C1+
xC2)![]() .
(11.84)
.
(11.84)
Частные решения
![]() находим по виду
правой части f(x)
= x
находим по виду
правой части f(x)
= x![]() :
в показателе степени
:
в показателе степени
![]() коэффициент при x
(a
=1) является корнем характеристического
уравнения кратности r=2,
многочлен
коэффициент при x
(a
=1) является корнем характеристического
уравнения кратности r=2,
многочлен ![]() = (x),
n=1,тогда
частное решение будем находить в виде
= (x),
n=1,тогда
частное решение будем находить в виде
![]() =
=
![]() (11.85)
(11.85)
Неопределенные коэффициенты A и В определяются в результате подстановки (11.85) в (11.81).
Производные:
![]() ;
(11.86)
;
(11.86)
![]() ;
(11.87)
;
(11.87)
После подстановки (11.85) - (11.87) в (11.81) имеем
![]() ;
(11.88)
;
(11.88)
Сокращаем на ![]() и приравниваем
коэффициенты при одинаковых степенях
х в
левой и правой частях уравнения (11.88),
получаем систему линейных уравнений
относительно А и В:
и приравниваем
коэффициенты при одинаковых степенях
х в
левой и правой частях уравнения (11.88),
получаем систему линейных уравнений
относительно А и В:
x: 2(3A + 2B) – 4B = 1;
![]() 2B
= 0;
2B
= 0;
откуда В = 0;
А =
![]() (11.89)
(11.89)
Подставляем (11.89) в (11.85):
![]() -
(11.90)
-
(11.90)
Частное решение ЛНДУ (11.81).
Общее решение ЛНДУ (11.81) с учетом формулы (22.82) и решений (11.84) и (11.90) принимает вид
![]() (11.91)
(11.91)
Сравниваем (11.91) и (11.79).
Общие решения, найденные предыдущими способами, совпадают.
11.53.
Проинтегрировать уравнение при начальных
условиях y=1,
![]() ,
при х = 0
,
при х = 0
![]() (11.92)
(11.92)
Решение Общее решение ЛНДУ (2.52) находим в виде
y
= ![]() +Y,(11.93)
+Y,(11.93)
где 1) Y – общее решение ЛОДУ
![]() +
+![]() - 2y=0;(11.94)
- 2y=0;(11.94)
характеристическое уравнение
λ² +λ -2 = 0,
D
= 1+8=9>0; корни:
![]() ;
тогда
;
тогда
![]() (11.95)
(11.95)
2)![]() -частное решение
ЛНДУ (11.92)- находим по виду правой части
-частное решение
ЛНДУ (11.92)- находим по виду правой части
f(x)=
![]() (11.96)
(11.96)
![]() - в
(11.96)
отсутствует, поэтому а=0;
коэффициенты при x
в (11.96) b=1;
- в
(11.96)
отсутствует, поэтому а=0;
коэффициенты при x
в (11.96) b=1;
![]() не являются корнями характеристического
уравнения; перед косинусом и синусом
в (11.96) –численные коэффициенты
(многочлены нулевой степени), тогда
частное решение находим в виде
не являются корнями характеристического
уравнения; перед косинусом и синусом
в (11.96) –численные коэффициенты
(многочлены нулевой степени), тогда
частное решение находим в виде
![]() =A
cosx
+ B
sinx,
(11.97)
=A
cosx
+ B
sinx,
(11.97)
где А и В – неопределенные коэффициенты;
дифференцируем (11.97):
![]() =- А sinx
+ B
cosx,(11.98)
=- А sinx
+ B
cosx,(11.98)
![]() = - А cosx
- B
sinx(11.99)
= - А cosx
- B
sinx(11.99)
Выражение (11.97) - (11.99) подставляем в (11.92), получаем
![]() ;
;
приравниваем коэффициенты при синусах и косинусах в левой и правой частях:
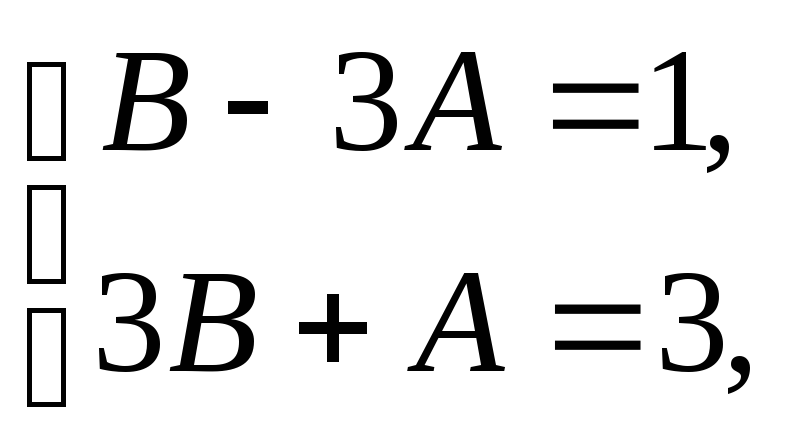
откуда А=0, В=1.
Таким образом, частное решение (11.97) имеет вид
![]() = sinx.(11.100)
= sinx.(11.100)
Подставляем (11.95) и (11.100) в (11.93), получаем общее решение ЛНДУ
![]() (11.101)
(11.101)
Находим далее частное решение, удовлетворяющее начальным условиям. Дифференцируем (11.101):
![]() (11.102)
(11.102)
Подставляем y=1;
![]() =2;x=0
в (2.61) и
(2.62):
=2;x=0
в (2.61) и
(2.62):
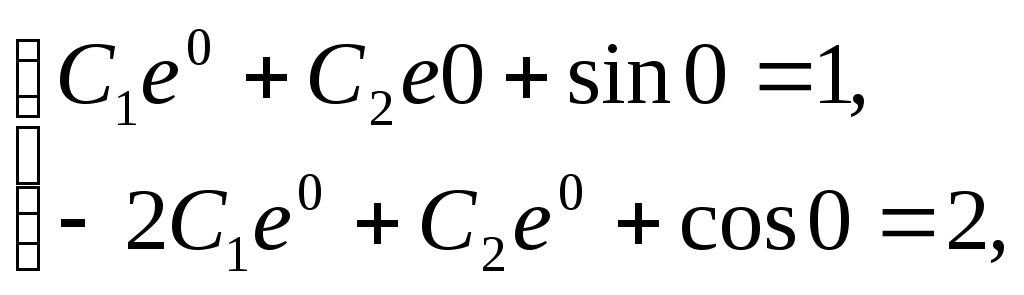 или
или
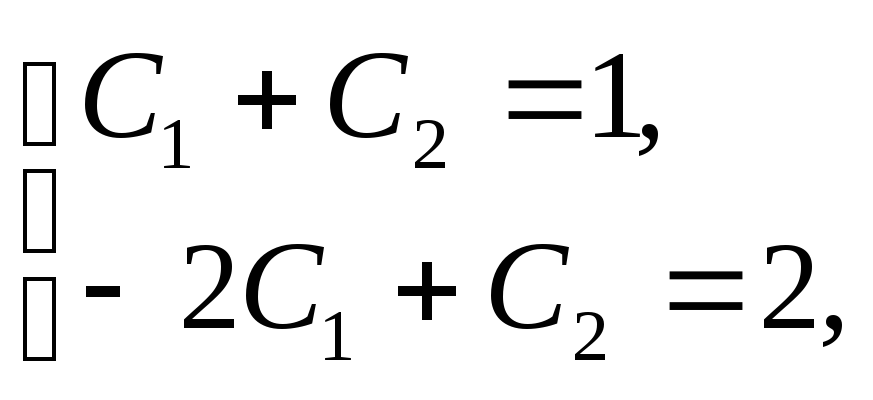
откуда ![]() частное решение
находим, подставляя полученные значения
произвольных постоянных в (11.101):
частное решение
находим, подставляя полученные значения
произвольных постоянных в (11.101):
![]() -
-
частное решение, удовлетворяющее начальным условиям.
