11. Дифференциальные уравнения
11.1. Дифференциальные уравнения первого порядка.
Дифференциальным уравнением (ДУ) первого порядка называется уравнение вида
F
( x;
y;
)
= 0,
(11.1)
где x
– независимая переменная, y
– зависимая
переменная,
–
ее производная.
Решением ДУ (1.1) называется всякая функция y = f (x), обращающая уравнение (1.1) в верное равенство.
Частным решением ДУ (1.1) называется решение, удовлетворяющее начальным условиям y = y0 при x = x0 .
Общим решением ДУ (1.1) первого порядка называется функция y = Y (x, c), где С – произвольная постоянная, удовлетворяющая двум условиям:
1) y = Y (x, c) является решением ДУ (1.1);
2) всякое частное решение получается из общего решения y = Y (x, c) при конкретном значении С.
Геометрическое общее решение ДУ – семейство кривых, называемых интегральными.
Процесс решения дифференциального уравнения называется его интегрированием.
Задача Коши: найти частное решение ДУ (1.1) при начальных условиях y = y0 при x = x0 .
Если общее решение представляется в неявном виде g(x; y; c) = 0 или g1 (x; y; c)=g2 (x; y), то оно называется общим интегралом, при конкретном значении С – частным интегралом.
Рассмотрим ДУ первого порядка, разрешенное относительно производной
= f
( x;
y),
(11.2)
где f – некоторая функция двух переменных (см. далее)
Теорема существования и единственности решения.
Пусть в ДУ (1.2)
функция f
(x;
y)
и ее частная производная
непрерывна
на открытом множествеG
координатной плоскости XOY.
Тогда:
Для всякой точки (x0 ; y0 ) множества G найдется решение y = y(x) ДУ (11.2), удовлетворяющее условию y = y0 при x = x0;
Если два решения y= y1(x) и y = y2 (x) уравнения (1.2) совпадают хотя бы для одного значения x = x0, то есть если y1(x0) = y2 (x0), то эти решения совпадают для всех тех значений переменной х, для которых они определены.
Геометрический смысл теоремы состоит в том, что через каждую точку (x0 ; y0) множества G проходит одна и только одна интегральная кривая ДУ (11.2).
Установим связь
между уравнением (11.2) и его интегральными
кривыми. Пусть f
(х;у) определена и непрерывна в области
G;
у = у(х) – интегральная кривая, проходящая
через точку M(х;
у). Проведем касательную к интегральной
кривой в точке М; α
– угол, образованный касательной МТ с
положительным направлением оси ОХ,
тогда tgα
=
(x)
(рис1.1), но
(x)
= f
(x,
y(x)
), тогда tgα
= f
(x,
y(x)
).
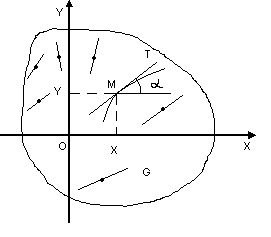
Рис 11.1
Таким образом, если через точку М(х;у) проходит интегральная кривая, то угол наклона касательной к ней в этой точке определяется формулой tgα = f (x, y).
Наклоны касательной можно указать, не находя интегральных кривых. Построим в каждой точке М € G отрезок, составляющий с положительным направлением оси ОХ угол α, тангенс которого tgα = f (x, y). Получим поле направлений, определяемой уравнением (1.2).
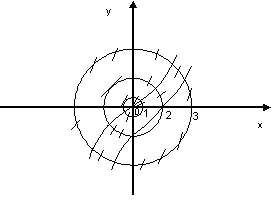
Кривая, в каждой точке которой направление поля ДУ (1.2) одно и то же, называется изоклинами этого уравнения. Уравнения изоклин f (x; y) = k, где k = tgα = const. Например, для уравнения y’= x² + y² изоклинами будут концентрические окружности x² + y² = k ( рис11.2)
