
- •11. Дифференциальные уравнения
- •11.1. Дифференциальные уравнения первого порядка.
- •Рис 11.1
- •Рис 11.2
- •11.2 Дифференциальные уравнения с разделяющимися переменными
- •Упражнения
- •Упражнения
- •11.4 Линейные ду первого порядка.
- •11.5 Уравнение Бернулли
- •Упражнения
- •11.6 Дифференциальные уравнения второго порядка.
- •11.7. Ду второго порядка, допускающее понижение порядка
- •Упражнения
- •11.8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лоду)
- •Упражнения
- •11.9. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лнду).
- •Упражнения
Упражнения
Найти общие решения.
 =
1/x;
=
1/x; = -
= - ;
; =
1- (
=
1- ( )²;
)²;x
 +
+ = 0;
= 0; =
sin x;
=
sin x; -
-
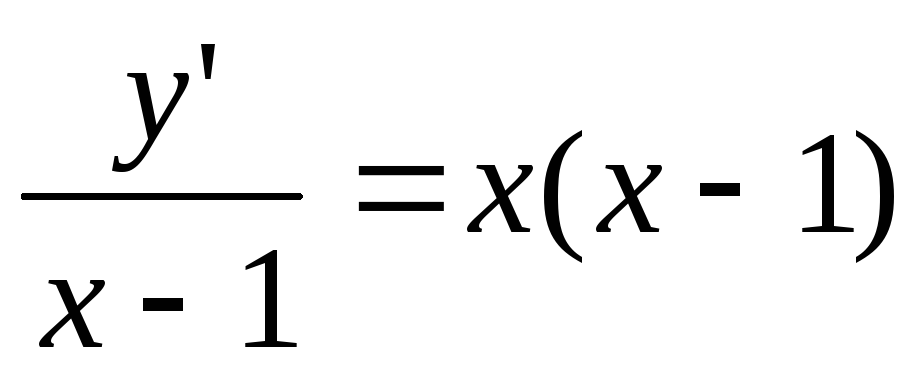 ;
;(1- x)²
 - x
- x =2;
=2; (2y+3) –
2(
(2y+3) –
2( )²
= 0
)²
= 0y
 –
– ²
= 0
²
= 0y
 –
(
–
( )²
= 0
)²
= 0
11.8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (лоду)
Линейное однородное ДУ второго порядка с постоянными коэффициентами имеет вид
![]() + p
+ p
![]() +qy
= 0, (11.53)
+qy
= 0, (11.53)
где p и q- действительные числа.
Можно доказать, что если y1(x) и y2(x) – линейно независимые*) частные решения ЛОДУ (2.13), то общее решение этого уравнения является их линейной комбинацией
y = C1y1(x) + C2y2(x), (11.54)
где С1 и С2 – произвольные постоянные числа.
Частные решения
можно найти в виде y =![]() (метод Эйлера), гдеλ
– действительное число.
(метод Эйлера), гдеλ
– действительное число.
Подставим y =![]() ,y’
= λ
,y’
= λ![]() и
и
![]() =
λ²
=
λ²![]() в ЛОДУ (11.53), сократим
в ЛОДУ (11.53), сократим![]() ,
получим
,
получим
λ² + pλ + q = 0 - (11.55)
характеристическое уравнение ЛОДУ (11.53).
Частные решения зависят от вида корней уравнения (11.53)
Если D = p² - 4q>0, то (11.55) имеет два действительных различных корня λ1
 λ2,
им
соответствуют частные решения
λ2,
им
соответствуют частные решения
y1(x)
=
![]() иy2(x)
=
иy2(x)
=
![]() (11.56)
(11.56)
Можно доказать, что функции(11.56) линейно независимы, тогда общее решение ЛОДУ (11.53) имеет вид
y
= C1![]() +C2
+C2![]() (11.57)
(11.57)
Если D = 0, то λ1=λ2 = λ, с качестве частных решений принимают линейно независимые функции
y1(x)
=
![]() иy2(x)=
x
иy2(x)=
x![]() ,
(11.58)
,
(11.58)
Общее решение:
y
= C1![]() +C2
+C2![]() ,
или
,
или
y
=
![]() (C1+
C2x)
(11.59)
(C1+
C2x)
(11.59)
Если D<0, то корни характеристического уравнения (11.55) комплексно- сопряженные
λ1,2
=
![]() ,
где
,
где![]()
Линейно независимые частные решения:
y1(x)
=
![]() sin
βx;
y2(x)=
sin
βx;
y2(x)=
![]() cos
βx.
(11.60)
cos
βx.
(11.60)
Общее решение:
y
=
![]() (C1sin
βx
+ C2cos
βx
). (11.61)
(C1sin
βx
+ C2cos
βx
). (11.61)
Примеры
Найти общее решение ЛОДУ
11.40
![]() –
5
–
5
![]() + 6y
= 0
+ 6y
= 0
Решение Составляем характеристическое уравнение:
λ² - 5λ + 6 = 0
Его дискриминант D>0, следовательно, квадратное уравнение имеет два действительных корня λ1 = 2; λ2=3, им соответствуют линейно независимые частные решения (2.16)
y1(x)
=
![]() иy2(x)
=
иy2(x)
=
![]()
и общее решение (2.17)
y
= C1![]() +C2
+C2![]()
11.41
![]() - 4
- 4
![]() +
4y
= 0.
+
4y
= 0.
Решение. Характеристическое уравнение λ² - 4λ + 4 = 0 имеет дискриминант D = 0 и два равных действительных корня λ1 = λ2=2; линейно независимые частные решения:
y1(x)
=
![]() иy2(x)=
x
иy2(x)=
x![]() .
.
Oбщее решение:
y
=
![]() (C1+
C2x).
(C1+
C2x).
11.42.
![]() +
+
![]() +
y
= 0
+
y
= 0
Решение. Характеристическое уравнение
λ² + λ + 1 = 0.
Дискриминант D<0. Корни:
λ1,2
=
![]() ;
;
линейно независимые частные решения:
y1(x)
=
![]() sin
sin
![]() x;
y2(x)=
x;
y2(x)=
![]() cos
cos![]() x.
x.
Общее решение:
y
=
![]() (C1sin
(C1sin
![]() x
+ C2cos
x
+ C2cos
![]() x
)
x
)
11.43. Найти частное решение, удовлетворяющее начальным условиям
y=1,
![]() =1, при х = 0,
=1, при х = 0,
![]() - 2
- 2
![]() + 2y
= 0.
+ 2y
= 0.
Решение. Характеристическое уравнение:
λ² - 2λ + 2 = 0
Дискриминант D = 4-8 = - 4<0. Корни характеристического уравнения:
λ1,2
=
![]() ;
;
Линейно независимые частные решения:
y1(x)
=
![]() sin
x; y2(x)=
sin
x; y2(x)=
![]() cosx.
cosx.
Общее решение:
y =
![]() (C1sin
x + C2cos
x) (11.62)
(C1sin
x + C2cos
x) (11.62)
Производная общего решения:
![]() =
=
![]() (
(C1-C2)sin
x + (C1-C2)
cosx ) (11.63)
(
(C1-C2)sin
x + (C1-C2)
cosx ) (11.63)
Подставляем
начальные условия y=1,
![]() =1,
при х = 0 в (11.62) и (11.63), получаем систему
линейных уравнений относительно C1
и C2:
=1,
при х = 0 в (11.62) и (11.63), получаем систему
линейных уравнений относительно C1
и C2:
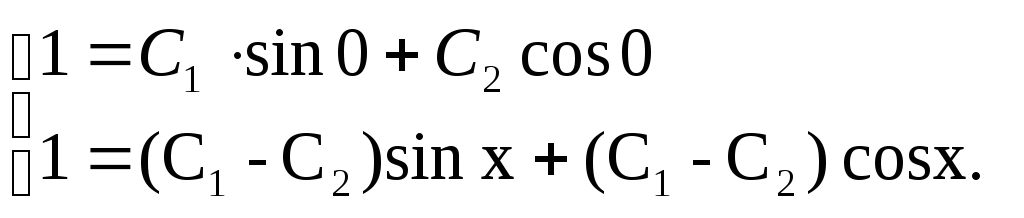 или
или
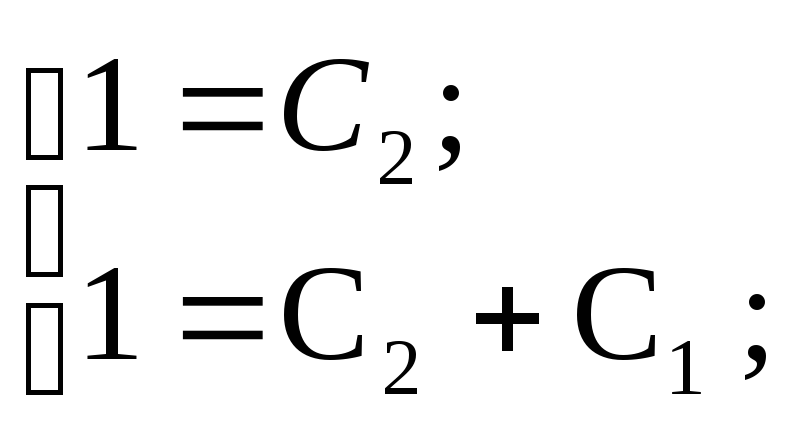 откуда
откуда
С1=0, С2=1. (11.64)
Значения (11.64) произвольных постоянных подставляем в общее решение (11.62):
![]() =
=
![]() (
0sin x + 1cos x ), или
(
0sin x + 1cos x ), или
y =
![]() cosx
–
cosx
–
частное решение исходного ЛОДУ, удовлетворяющее начальным условиям.
