Уравнения бокового движения.

Так как силы и моменты, определяющие боковое движение, существенно зависят от , V и H, т.е. параметров продольного движения, то в общем случае рассматривать уравнения бокового движения изолированно от продольного нельзя. Но если при движении ЛА величину скорости, высоту, углы атаки и тангажа можно считать постоянными (медленно меняющимися), т.е. Vconst, Hconst, ₀=const, ₀=const, а сам ЛА имеет плоскость аэродинамической, массовой и инерционной симметрии, то из общей системы уравнений пространственного движения можно выделить уравнения, описывающие параметры бокового движения. Учитывая, что требование постоянства угла тангажа эквивалентно , или , то при , и уравнения бокового движения примут вид

,

, или ,

,

,

,

,

где угол скольжения, от которого зависит боковая сила, можно найти из соотношения

,

а скоростной угол крена –

,

или .

Строго говоря, полученные уравнения не являются уравнениями изолированного бокового движения, так как в них входят параметры продольного движения, которые, в свою очередь, меняются при боковом движении.

Например, если ЛА совершал полет без крена с постоянными углами и , то после поворота по крену на угол подъемная сила повернется на угол . Это приведет не только к появлению горизонтальной «боковой» составляющей , но и к уменьшению составляющей в вертикальной плоскости. Из-за этого изменится угол наклона траектории, т.е. - перестанет быть равным . Чтобы сохранить значение , необходимо изменить величину подъемной силы, но для этого надо изменить угол атаки, из-за чего изменится угол тангажа, т.е. - перестанет быть равным .

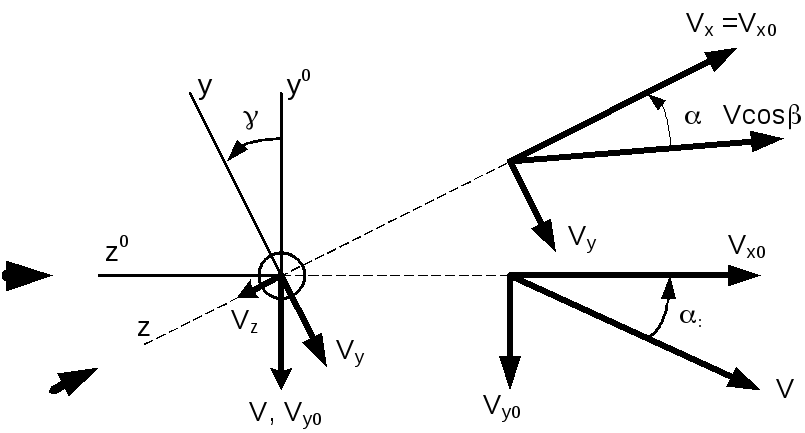
Следует также учитывать, что при крене ЛА углы атаки и скольжения меняются из-за поворота плоскости симметрии ЛА относительно вектора скорости, т.е. – кинематически. Например, если ЛА совершает полет без скольжения с углом ₀, и повернулся по крену на угол , то при этом появится угол скольжения, а угол атаки – изменится. Величины углов атаки  и скольжения  после поворота можно найти по проекциям скорости на оси связанной СК до и после поворота по крену, обозначив их соответственно , , и , , :

,

(см. рисунок, на котором справа показаны проекции скорости на плоскость симметрии до и после поворота на угол ). Для малых ₀ эти соотношения можно заменить на приближенные   ₀ cos,   ₀ sin.

Все эти изменения можно попытаться скомпенсировать управлением в продольном канале, создавая соответствующие моменты и силы, однако, это не всегда возможно, а главное – вряд ли разумно.

Поэтому пользоваться уравнениями бокового движения нужно очень осмотрительно.

Если полет происходит близко к горизонтальной плоскости, а углы атаки пренебрежимо малы, т.е. ₀0, ₀0, ₀0, то уравнения бокового движения приобретают вид

, , или ,

, ,

,

,

,

,

или , т.е. .

При таком движении

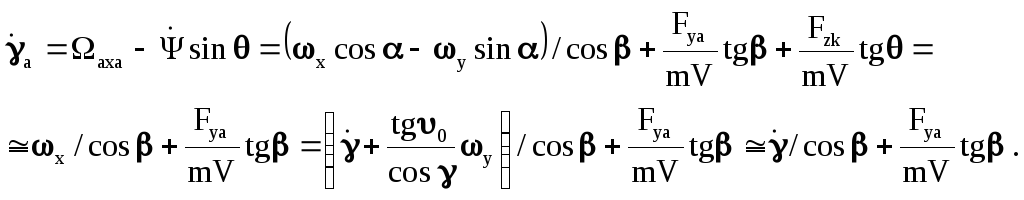
При горизонтальном полете вертикальная составляющая суммарной силы равна нулю, однако, составляющая по оси y_a вполне может оказаться не нулевой . Поэтому более удобным в данном случае оказывается соотношение .

Соотношения для угла скольжения и скоростного угла крена в этом случае достаточно просто получить непосредственно.

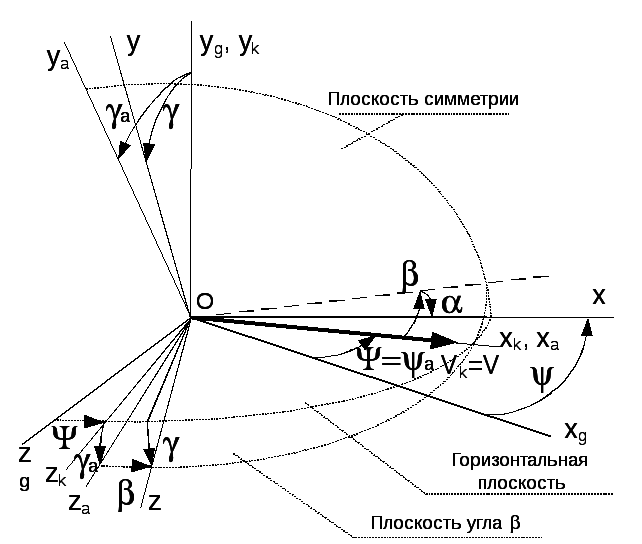
Угол определяется из совпадения осей y и y_a связанной и скоростной СК при нулевом крене, т.е. из того, что , откуда , а углы скольжения и атаки - из рассмотрения осей x_g, x_k, x_a, x и проекции скоростной оси на плоскость симметрии: , .

Из этого же рассмотрения можно увидеть, что в этом случае достаточно просто выражаются проекции на оси траекторной системы координат тех сил, которые определены в связанной СК. В частности, для силы тяги, задаваемой обычно проекциями на оси связанной СК, , поэтому уравнение для угла пути можно записать в виде

.

И, наконец, если при тех же условиях ЛА движется без крена (с пренебрежимо малым креном), то

,

, или ,

,

,

.

Разделение движения на угловое и траекторное (поступательное)

В общей системе уравнений движение центра масс (траекторное, или поступательное) и движение вокруг ЦМ (угловое) и описываются отдельными группами уравнений, но просто разделить эту систему на эти две группы в общем случае нельзя - в уравнения поступательного движения входят углы , , , а также  и  (в аэродинамические силы), а аэродинамические моменты, определяющие движение вокруг ЦМ, зависят от V и H. Разделение движений возможно лишь при некоторых упрощающих предположениях или выполнении ряда упрощающих условий.

Выделение уравнений углового движения

Из общих уравнений движения очевидно, что параметры углового движения никак не зависят от переменных x и z. Если предположить, что параметры углового движения меняются гораздо быстрее, чем меняется высота и модуль скорости полета, т.е. Vconst, Hconst, то для углового движения общую систему можно рассматривать без первых четырех уравнений. Предположив (как это уже было сделано выше) отсутствие ветра, можно заменить уравнения для изменений угла наклона траектории и угла пути , на уравнения для изменений углов атаки и скольжения . Полученную в результате систему

,

,

,

,

,

,

,

можно рассматривать как уравнения пространственного углового движения.

Так как ,

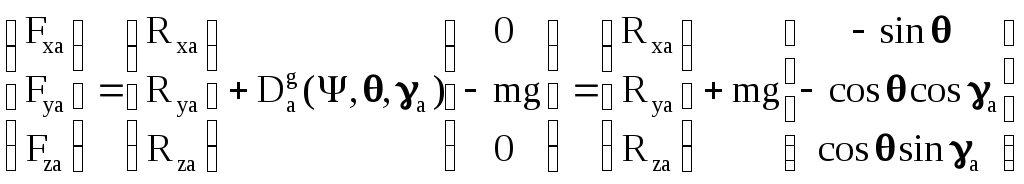а ,

,

то

,

,

Если пространственное маневрирование осуществляется с большими перегрузками, то силой тяжести можно пренебречь по сравнению с результирующей силой, и для рассмотрения углового движения достаточно системы из пяти уравнений

,

,

,

,

.