КФ МГТУ им. Н. Э. Баумана
Калужский филиал
Упражнение № 2
Методические указания
Калуга 2014
Упражнение №2
Преобразование логических функций.
Цель работы: освоить методы преобразования логических функций.
Задание: изучить теоретические сведения, выполнить все задания упражнения и продемонстрировать преподавателю, оформить результаты выполнения в виде отчёта.
Содержание отчёта: сформулировать цель работы, теоретические сведения, решения заданий упражнения, заключение.
Теоретические сведения.
Метод карт Карно.
Пусть логическая функция задана таблицей истинности:
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Дизъюнктивная нормальная форма (ДНФ)– это форма представления, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждый из которых является простой конъюнкцией аргументов или их инверсий.
Если в каждом члене ДНФ представлены все аргументы (или их инверсии) функции, то такая форма носит название совершенной дизъюнктивной нормальной формы (СДНФ). Для любой функции алгебры логики существует своя единственная СДНФ.
Для того чтобы найти
СДНФ, отметим строки таблицы, в которых
.
Рассмотрим значения переменных, при
которых функция принимает единичное
значение. Если значение переменной
равно 0, то она записывается в СДНФ с
инверсией, если 1 – то без инверсии.
Пользуясь данным правилом, найдём СДНФ, используя таблицу истинности представленную выше:
Здесь для краткости записи операция конъюнкции (логическое И, логическое умножение, &) используется символ ”·”, который опущен. Операция дизъюнкции (логическое ИЛИ) обозначается символом ”|”. Части СДНФ, объединённые дизъюнкцией называются термами.
Недостаток СДНФ в том, что она слишком громоздкая. Для упрощения СДНФ и СКНФ могут использоваться несколько методов. Все они основаны на операциях попарного неполного склеивания и элементарного поглощения.
Рассмотрим метод минимизации с использованием карт Карно.
Таблица истинности функции преобразуется в карту Карно. Логические переменные группируются в столбцы и строки. Соседние столбцы и соседние строки могут отличаться не более чем в одном элементе.
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
1 |
|
|
|
1 |
|
|
1 |
В карте Карно необходимо отыскать области, пригодные для склеивания.
Области должны удовлетворять следующим условиям:
- они должны содержать в себе 1, если требуется получить ДНФ и 0, если требуется КНФ;
- площадь области единиц должна быть 2n, где n – целое число, и область должна быть симметрична относительно центра;
- в области должны содержаться только 1;
- все 1 должны принадлежать какой-либо области;
- общее число областей должно быть минимальным, а число 1 в областях максимальным;
- одна ячейка карты Карно может входить в несколько областей;
- крайние клетки каждой горизонтали и каждой вертикали также граничат между собой.
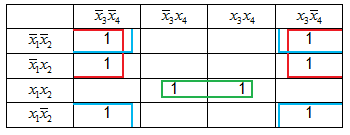
После нахождения всех областей каждая их них рассматривается отдельно. Неизменные переменные в области выписываются с конъюнкцией, изменяющиеся переменные отбрасываются. Конъюнкции всех областей соединяются дизъюнкцией:
Метод Квайна.
Метод Квайна позволяет преобразовать СДНФ в минимальную ДНФ.
Наример минимизируем функцию:
Производится переход к сокращённой форме перебором возможных комбинаций склеивания и поглощения. Если функции отличаются только одной переменной, то они записываются в правый столбик. Отличающийся элемент заменяется ” * ”.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Члены сокращенной формы называют простыми импликантами функции.
Сокращенная форма может содержать лишние члены, исключение которых из выражения функции не повлияет на значение функции. Поэтому далее строят импликантную матрицу:
|
Простые импликанты |
Члены СДНФ |
|||||
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
x |
x |
Простые импликанты, которые не могут быть лишними и не могут быть исключены – составляют ядро. Входящие в ядро импликанты легко определяют по матрице: для каждого ядра есть хотя бы 1 столбец, перекрываемый только одной импликантой. Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их количество с минимальным вхождением букв в каждую, которые обеспечивают перекрытие всех столбцов импликантной матрицы не перекрытых членами ядра.
Недостаток метода Квайна – необходимость полного попарного сравнения всех термов на этапе нахождения первичных импликант.
Метод Квайна-Мак-Класки.
Представляет собой улучшенную версию предыдущего метода.
Рассмотрим данный метод на примере преобразования функции
На первом шаге заменим
отрицания нулями, обычные переменные
единицами:
На втором шаге перегруппируем логические функции. Номер группы будет соответствовать количеству единиц в терме (табл. 1):
Таблица 1.
|
Номер группы |
|
|
1 |
0001 |
|
2 |
0011, 0101 |
|
3 |
0111, 1110 |
|
4 |
1111 |
На третьем шаге склеиваются соседние строки таблицы 1, в которых различается ровно 1 элемент. Отличные элементы обозначим '*'. Склеившиеся номера обозначаем цветом. Перестроим таблицу. Результат показан в таблице 2.
Таблица 2.
|
Номер группы |
|
|
1 |
00*1, 0*01 |
|
2 |
0*11, 01*1 |
|
3 |
*111, 111* |
Производим аналогичное склеивание в таблице 2. Сравнивать термы можно только в том случае, если у них ”*” находятся в одинаковых позициях. Результат показан в таблице 3.
Таблица 3.
|
Номер группы |
|
|
1 |
0**1 |
Неотмеченные после склеивания номера являются простыми импликантами:
*111, 111*, 0**1.
Далее строим импликантную матрицу для получения минимальной логической функции:
|
Простые импликанты |
Члены СДНФ |
|||||
|
|
|
|
|
|
|
|
|
|
x |
x |
x |
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
x |
x |
По таблице определяем
совокупность простых импликант: 0**1 и
111*, и соответствующую им минимальную
ДНФ:
Таким образом,
