
lekcii toe
.pdf
|
|
|
|
|
− J |
|
Следовательно, изображение |
сингулярной составляющей X − ( p) = ∑S j p − j . |
|||||
|
|
|
|
|
j =0 |
|
Изображение регулярной составляющей X + ( p) = |
B( p) |
. Тогда |
||||
A( p) |
||||||
|
|
|
|
|||
|
− J |
|
|
− J |
||
- [X − ( p)]= - ∑S j p − j = |
∑S j δj = x − (t) |
|||||
|
j =0 |
|
|
j =0 |
||
|
|
′ |
|
|||
Выделение целой части из |
дроби |
B ( p) |
означает отделение изображения |
|||
|
|
|
||||
A( p)
сингулярной составляющей реакции, перевод которой в t-область не представляет затруднений. Следовательно, необходимо далее перевести в t-область изображение
регулярной составляющей |
X + ( p) = |
B( p) |
|
и следовательно ее можно разложить в сумму |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вида: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
+ |
( p) = |
|
|
a1 |
|
|
+ |
|
|
|
a2 |
|
|
|
|
+ ... + |
|
|
ak |
|
|
|
+ ... + |
|
an |
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p − p1 |
p − p2 |
|
|
|
|
p − pk |
|
|
|
|
|
|
|
p − pn |
|
|
||||||||||||||||||
|
Где |
|
p1... pn - корни полинома |
|
A( p) |
|
среди которых нет кратных, |
а коэффициенты |
||||||||||||||||||||||||||||||||||||||||||
a1...an - неизвестны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
До множим обе части на p − pk : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
( p − pk ) X |
+ |
( p) = |
|
a1 ( p − pk ) |
+ |
a2 |
( p − pk ) |
+ ... |
+ ak |
+ ... + |
an ( p − pk ) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
p − p1 |
|
|
|
|
|
|
p − p2 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p − pn |
|||||||||||||
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a |
|
= lim ( p − p |
|
) X + ( p) = lim ( p − p |
|
) |
B( p) |
|
k = 1...n . |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
k |
k |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p→ pk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p→ pk |
|
|
|
|
|
|
A( p) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Если среди корней полинома A( p) |
|
есть кратные, то тогда появятся слагаемые вида: |
|||||||||||||||||||||||||||||||||||||||||||||||
... + |
ak |
|
+ |
ak +1 |
|
+ ... , |
|
то в этом случае по формуле Хевисайда вычисляют старший |
||||||||||||||||||||||||||||||||||||||||||
p − p |
k |
( p − p |
k |
)2 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim ( p − p |
|
|
2 |
|
|
|
+ |
( p) = lim ( p − p |
|
|
2 |
B( p) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
k |
+1 |
k |
) |
|
X |
|
k |
) |
|
|
|
|
|
, |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p→ pk |
|
|
|
|
|
|
|
|
|
|
|
|
p→ pk |
|
|
|
|
|
|
|
A( p) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
а ak |
вычисляют по методу неопределенных коэффициентов. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
В результате изображение регулярной составляющей X + ( p) может быть записано в |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
ai |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
виде суммы ∑ |
|
|
, где ai |
- известны. И тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
p − p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- [X + ( p)] |
|
|
|
|
|
|
n |
|
|
|
|
ai |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
= - ∑ |
|
|
|
|
|
= ∑ai e pit = x+ (t) . |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
p |
− pi |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− J |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
- [X ( p)]= - [X − ( p) + X + ( p)]= ∑S j δj + ∑ai e pit = x− (t) + x + (t) = x(t) . |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j =0 |
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Корни полинома A( p) |
называют полюсами функции X ( p) . Коэффициенты a1...an - |
||||||||||||||||||||||||||||||||||||||||||||||||
вычетами, |
ak - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
называют нулями функции |
||||||||||||
вычет в полюсе pk . Корни полинома B ( p) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
X ( p) .
41
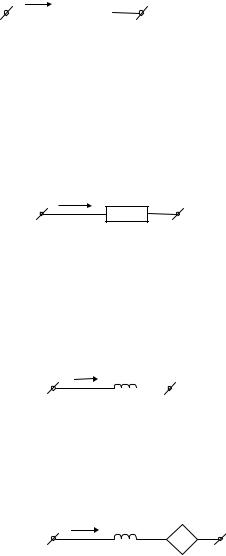
§3. Уравнения Ома и Кирхгофа для элементов цепи и уравнения Кирхгофа для элементов цепи в операторной форме. Операторная схема замещения элементов и цепей. Анализ пассивных и активных линейных цепей с помощью их операторных схем замещения
Уравнения Ома и Кирхгофа в операторной форме для элементов цепи
Резистор
Для линейного резистора в t-области уравнения ВАХ выглядят так:
i(t) |
R |
u(t) = Ri(t) |
|
|
i(t) = Gu(t) |
|
|
+ u(t)
Преобразуем их по Лапласу и получим:
U ( p) = RI ( p) и I ( p) = GU ( p) .
Следовательно, для операторного сопротивления и проводимости:
Z ( p) = R и Y ( p) = G .
I ( p) R
+ U ( p)
Индуктивность
Для линейной индуктивности в t-области уравнения ВАХ выглядят так:
i(t) |
L |
|
u(t) = LDi(t) |
+ |
u(t) |
|
i(t) = L−1 D −1u(t) |
|
|||
|
|
Преобразуем первое уравнение по Лапласу и получим:
U ( p) = pLI ( p) − Li(0− ) , операторное сопротивление Z ( p) = pL
Li(0− )
I ( p) pL
+
+U ( p)
Преобразуем второе уравнение по Лапласу и получим:
I ( p) = |
1 |
U ( p) + |
i(0− ) |
, операторная проводимость Y ( p) = |
1 |
|
pL |
p |
pL |
||||
|
|
|
42

I ( p)
+ |
|
|
|
U ( p) |
1 |
i(0− ) |
|
pL |
p |
||
|
Емкость
Для линейной емкости в t-области уравнения ВАХ выглядят так:
i(t) C i(t) = CDu(t)
u(t) = C −1D−1i(t)
+ u(t)
Преобразуем первое уравнение по Лапласу и получим:
I ( p) = pCU ( p) − Cu(0− ) , операторная проводимость Y ( p) = pC .
I ( p)
+ |
|
|
U ( p) |
pC |
Cu(0− ) |
Преобразуем второе уравнение по Лапласу и получим:
U ( p) = |
1 |
I ( p) + |
u(0− ) |
, операторное сопротивление Z ( p) = |
1 |
. |
pC |
p |
|
||||
|
|
|
pC |
|||
1u(0− )
|
|
|
|
p |
I ( p) pC |
||||
|
|
|
|
+ |
|
|
|
|
|
+
U ( p)
Уравнения Кирхгофа для элементов структуры цепи
В t-области:
для контура ∑uk (t) = 0 .
k
для узла ∑im (t) = 0 .
m
В p-области:
для контура ∑[U k ( p) + Qi ( p)] = 0 ,
k
для узла ∑[I m ( p) + Ql ( p)] = 0 ,
m
где U k ( p) и I m ( p) - изображения соответствующих напряженийuk (t) и токов im (t) ,
Qi ( p) и Ql ( p) - это векторы (столбцы), учитывающие ненулевые начальные условия.
43
Процедура анализа линейных цепей с помощью операторных схем замещения
1.Обычным образом в t-области анализируем цепь до коммутации и находим предначальные значения токов в индуктивностях и напряжений на емкостях.
2.По Лапласу преобразуем входные воздействия.
3.Замещаем все индуктивности и емкости их операторными схемами, выбирая те из них, которые приводят к более простым структурным схемам, и строим операторную схему цепи.
4.Полученную операторную схему цепи обычным образом описываем алгебраическими уравнениями Кирхгофа относительно изображений искомых переменных.
5.Обычным образом проверяем условия существования и единственности решения составленной системы алгебраических уравнений. Решаем эту систему уравнений и
витоге находим изображения искомых переменных
6.Найденные изображения с помощью теоремы Хевисайда переводим в оригиналы.
7.Проверка. Полученное решение подставляем в исходные уравнения и обращаем их
втождества. Если проверка не прошла, то приступаем к поиску ошибок.
§4. Анализ пассивных и активных линейных цепей путем преобразований по Лапласу дифференциально-интегральных уравнений Кирхгофа
Опишем цепь уравнением Кирхгофа:
A(D) x(t) = G(D) f (t) + H 0 |
(1) |
||
Преобразуем это уравнение по Лапласу: |
|
|
|
A( p) X ( p) = G( p)F ( p) + p−1H |
0 |
+ Q( p) = C( p) |
(2) |
|
|
|
|
где Q( p) - вектор предначальных условий. |
|
|
|
A( p) X ( p) = C( p) X ( p) = A−1 ( p)C( p) |
(3) |
||
Процедура анализа:
1.Обычным образом анализируем цепь до коммутации и находим предначальные значения токов через индуктивности и напряжений на емкостях.
2.Обычным образом в t-области формируем уравнение (1), в частности в этом
уравнении H 0 может быть равно нулю. Обычным образом проверяем условия существования и единственности решения.
3.Уравнение (1) преобразуем по Лапласу и получаем уравнение (2), решаем его и получаем уравнение (3).
4.Найденные изображения X ( p) с помощью теоремы Хевисайда преобразуем в
оригиналы x(t) .
5. Проверка. Полученные выражения подставляем в исходные уравнения и обращаем их в тождества. Если проверка не прошла, то приступаем к поиску ошибок.
§5. Анализ пассивных и активных линейных цепей путем преобразования по Лапласу дифференциальных уравнений состояния
Составляем уравнение состояния:
Dx(t) = Ax(t) + Bf (t) |
(1) |
Преобразуем это уравнение по Лапласу: |
|
pX ( p) − x(0− ) = AX ( p) + BF ( p) |
(2) |
44
[pE − A]X ( p) = x(0− ) + BF ( p) X ( p) = [pE − A]−1 [x(0− ) + BF ( p)] |
(3) |
Процедура анализа:
1.Обычным образом анализируем цепь до коммутации и находим предначальные значения токов через индуктивности и напряжений на емкостях.
2.Обычным образом формируем уравнение состояния (1).
3.Сформированное уравнение (1) преобразуем по Лапласу и получаем уравнение (2) решаем его и получаем уравнение (3).
4.Найденные изображения X ( p) с помощью теоремы Хевисайда переводим в
оригиналы x(t) .
5. Проверка. Полученные выражения подставляем в исходные уравнения и обращаем их в тождества. Если проверка не прошла, то приступаем к поиску ошибок.
§6. Передаточная функция. Связь передаточной функции с импульсной и переходной характеристиками цепи
Передаточная функция
Передаточной функцией цепи называется отношение изображения какой-либо из ее реакций к изображению входного сигнала при нулевых предначальных условиях.
По определению H ( p) = X ( p) = B′( p) = Φ(R, L, C, K , p) . Она может быть получена
F ( p) A( p)
как результат операций в p-области над уравнениями, описывающими динамику цепи, и представляет собой алгебраическую величину.
Связь передаточной функции цепи с импульсной характеристикой
H ( p) = X ( p)
F ( p)
f (t) = δ0 (t) = 1 = F ( p) x(t) = h0 (t) = H 0 ( p)
H ( p) = H 0 ( p) = H 0 ( p) 1
Передаточная функция H ( p) есть изображение импульсной характеристики цепи
h0 (t) .
Связь передаточной функции с переходной характеристикой цепи
H ( p) = X ( p)
F ( p)
f (t) = δ1 (t) = 1 p = F ( p) x(t) = h1 (t) = H1 ( p)
H ( p) = H1 ( p) = pH1 ( p) = H 0 ( p) 1 p
H1 ( p) = p −1 H ( p) = p −1 H 0 ( p)
Общее замечание
Если цепь кусочно-линейная (характеристики элементов заданы по кускам), то переход с одного участка линейности на другой равносилен коммутации. Поэтому в начале каждого участка линейности необходимо найти предначальные условия, изменить параметры элементов и обычным образом продолжить решение этого нового участка линейности, с соответствующими статическими характеристиками элементов.
45
