Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

lekcii toe

.pdf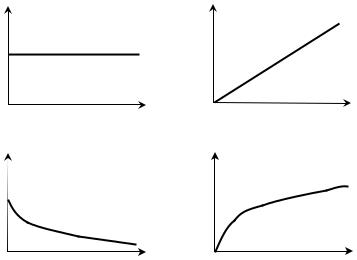

Скачиваний:

Добавлен:

09.02.2015

Размер:

524.26 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

4.Проверяем условие существования и единственности решения уравнения (4): det[DE − A] ≠ 0 и решаем уравнение (4) с точностью до постоянных интегрирования.

5.Анализируем цепь до коммутации и находим предначальные условия iLm (0− ) и

uCm (0− ).

6.По правилу коммутации находим начальные значения iLm (0+ ) и uCm (0+ ).

7.По уравнениям состояния и вытекающим из него уравнениям находим N − 1 начальное условие для старших производных от переменных состояния, где N – порядок цепи.

8.Формируем алгебраическую систему уравнений относительно постоянных интегрирования, решаем ее и записываем окончательный ответ.

9.Проверка. Полученные решения подставляем в исходные уравнения и обращаем их в тождества. Если проверка не прошла, то приступаем к поиску ошибок.

10.Если проверка прошла успешно, то строим эквивалентную схему замещения, в которой к R-цепи подключены независимые источники и зависимые взамен емкостей и индуктивностей, с известными теперь напряжениями и токами и любым удобным способом находим искомые реакции, не являющиеся переменными состояния.

§5. Пробные сигналы. Единичная ступенчатая функция Хевисайда. Единичная импульсная функция Дирака. Обобщенная производная и обобщенная функция. Переходная и импульсная характеристики цепи.

Пробные сигналы

f (t )

F (t )

F (t ) = D −1 f (t )

x(t )

X (t )

X (t ) = D −1 x(t )

Если для линейной цепи известна реакция на один сигнал, то непременно можно построить процедуру, которая позволит вычислить реакцию на любой сигнал.

Отсюда сделует, что нужно решить две задачи:

1.Подобрать хороший пробный сигнал.

2.Построить аппарат с использованием этого сигнала, который позволил бы эффективно вычислять реакцию на любой другой сигнал, если известна реакция на пробный.

Единичная ступенчатая функция Хевисайда

Требованиям предыдущего пункта удовлетворяет, например, функция Хевисайда

δ (t ) = 0, t < 0 .		δ1 (t )
1	1, t ≥ 0
	1, t ≥ 0
Преимущества		1

•простая,

•частные решения ДУ — константы,

• легко модифицировать под конкретные	0	t
нужды (например, ввести δ1(−t), δ1(t − τ) —	0
нужды (например, ввести δ1(−t), δ1(t − τ) —
см. рис.),	δ1 (− t )

•с ее помощью можно «вырезать» части

других функций (см. рис),

•предначальные условия при использовании в качестве пробного сигнала всегда равны

нулю (из определения δ1(t)).	0	t

		f (t )δ1 (t − τ)			f (t )δ1 (t − τ1 )(τ2 − t )
0	τ	t	0	τ1 τ	t
0	τ		0	τ1 τ	2

δ1 (t − τ)

0	τ	t

Единичная импульсная функция Дирака

		φ(t )					Dφ(t )	2					D 2 φ(t )
		φ(t )					Dφ(t )								4
		1													4
		1						τ							τ2	τ
																2
		0					0		τ	t				0			t

−	τ		τ	t	−	τ					−	τ
			τ									τ
								2
2			2		2			2			2		−	4
														4
														τ2
														τ2
		δ (t )					δ (t )						δ−1 (t )
		1					0
		1					0

		0		t						t				0			t

Единичная импульсная функция Дирака (она же δ-функция Дирака) представляет собой бесконечно короткий импульс бесконечно большой высоты с площадью, равной единице. Естественно, что дельта-функция — математическая абстракция, и на практике не осуществима. Но это полезная абстракция, т.к. близкие к ней сигналы осуществить можно.

Введем дельта-функцию формально. Пусть

t >

t +

+ 0,5

t −

; 0

φ(t ) =

t −

+ 0,5

t < −

Тогда

t t

−

; 0

Dφ(t )

−

t t 0;

< −

t −

; 0

φ(t ) = −

t 0;

t < −

, t

Из рисунка очевидно, что

lim φ(t ) = δ1 (t ) .

τ→0

Такое описание функции δ1 (t ) соответствует уже данному ранее определению. Также очевидно, что

lim Dφ(t ) = ∞		t = 0
τ→0	0	t < 0 , t > 0
τ→0

Эту функцию назовем единичной импульсной функцией Дирака.

1.	δ0	(t ) = ∞ t = 0
		0 t < 0 , t > 0
	0+
2.	∫δ0 (t )d t = 1
	0−
Это функция Дирака нулевого порядка или δ-функция.

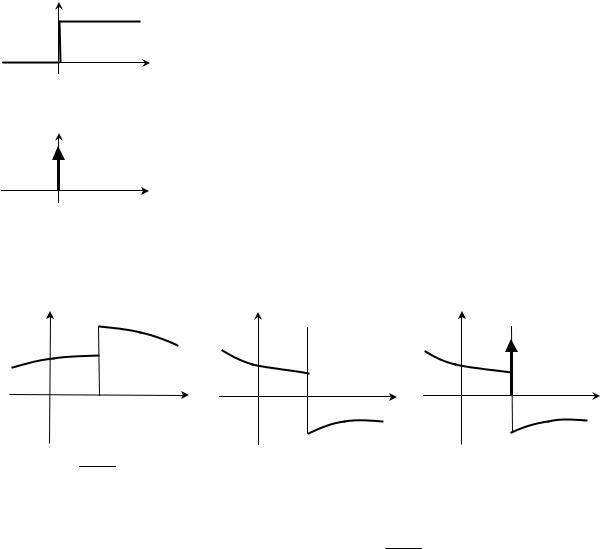
Функция δ−1 (t ) называется функцией Дирака −1 порядка.

1. δ−1 (t ) = ± ∞ t = 0

0 t < 0 , t > 0

2.∫δ−1 (t )d t = 0

0−

Достаточно очевидны следующие соотношения:

δ0 (t ) = Dδ1 (t ), δ−1 (t ) = Dδ0 (t ) = D 2 δ1 (t ) .

Обобщенная производная и обобщенная функция

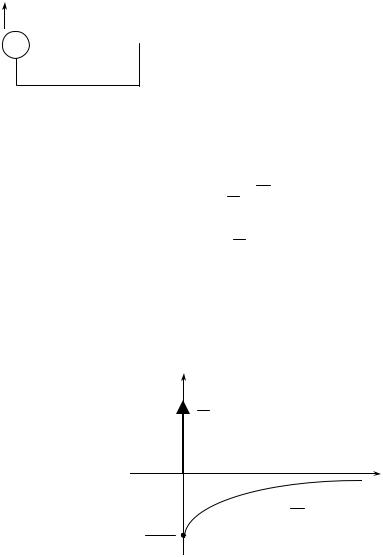
Обобщенная производная совпадает с классической, ньютоновской производной всюду, где дифференцируемая функция непрерывна и дополняет там, где дифференцируемая функция имеет разрывы первого рода. Это дополнение имеет вид функций Дирака. Определим весовые коэффициенты этих дополняющих функций.

δ1 (t )

Dδ1 (t ) = δ0 (t ) t = 0

0 t

		dδ1	(t )	= 0 t ≠ 0
δ0 (t )		dt		= 0 t ≠ 0
		dt

0	t

δ0 (t ) = Dδ1 (t ) = [δ1 (0+ )− δ1 (0− )]δ0 (t ) = [1 − 0]δ0 (t ) = δ0 (t )

Из этого рассмотрения следует, что весовой коэффициент δ-функции в точке разрыва равен разности значений, дифференцируемой функции справа и слева от точки разрыва.

f (t )	f (τ− )		d f (t )		Df (t )		[f (τ + )− f (τ− )]δ		(t − τ)
								0
	f (τ+ )		dt


0	τ	t	0	τ	t	0	τ	t

Символом d f (t ) будем обозначать классическую производную. dt

Символом Df (t ) будем обозначать обобщенную производную.

И тогда эту обобщенную производную можно определить следующим образом:

Df (t ) = [f (τ+ )− f (τ− )]δ0 (t − τ) + d f (t ) dt

Из проделанного обобщения следует, что могут быть определены и обобщенные функции, которые состоят из импульсных и непрерывных составляющих. Импульсные составляющие назовем сингулярными, а непрерывные составляющие — регулярными. Тогда запишем обобщенную функцию в виде:

− J

f (t ) = f − (t ) + f + (t ) = ∑S j δj (t − τ j )+ f + (t )

j =0

где S j - весовые коэффициенты импульсных функций, J - это предельный порядок

импульсных функций, τ	j	- моменты разрыва первого рода, f + (t ) - аналитическая
	j

функция (имеющая разложение в ряд Тейлора).

Переходная и импульсная характеристики цепи

Переходной характеристикой называется реакция цепи на единичное воздействие при нулевых предначальных условиях, и обозначается h1 (t ) .

Импульсной характеристикой называется реакция цепи на единичное импульсное воздействие при нулевых предначальных условиях, и обозначается h0 (t ) .

В силу линейности цепи реакции на единичное и единичное импульсное воздействие связаны:

h0 (t ) = Dh1 (t )

В общем случае, когда переходная характеристика имеет разрыв первого рода:

h0 (t ) = Dh1

(t ) = h1

)δ0 (t ) +

d h1 (t )

−

(t )

(t ) .

= h0

+ h0

d t

В том случае, когда переходная характеристика имеет ненулевое начальное

значение, то при t = 0+ появляется сингулярная составляющая h

(0+ )δ (t ) .

Пример

i(t)

Дано:

R, C

u(t)

Найти:

i(t ) t ≥ 0

1) h1(t), 2) h0(t)

1) u(t ) = δ1 (t )

uC (0− ) = 0

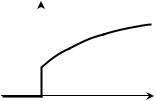
Решив задачу по сформированной в §4 процедуре, получим

uC (t ) = 1 e R

h1 (0+ ) = 1

− 1 t

RC = h1 (t )

2) u(t ) = δ0 (t )

uC (0− ) = 0

h0 (t ) = Dh1 (t ) = h1 (0+ )δ0 (t ) −

Графически

−

R 2 C

1	−	1	t	1

	e RC =
RC 2				R

1 δ0 (t ) = h0− (t )

−	1	−
		e
	R2C	e
	R2C

			1		−	1	t
δ		(t ) −	1	e		RC = h − (t ) + h + (t ).
δ	0	(t ) −		e		RC = h − (t ) + h + (t ).
	0		RC 2		0			0
			RC 2

1 t

RC = h0+ (t )

Особый случай правила коммутации

Особый случай правила коммутации возникает, когда в цепи действуют импульсные функции токов и напряжений. В этом случае законы непрерывности потока сцепления и заряда перестают действовать и необходимо ввести дополнения, которые бы позволили находить начальные значения токов в индуктивностях и напряжений на емкостях.

Предположим, что через емкость протекает δ-функция тока: iC (t ) = S0 δ0 (t ) , тогда при

t = 0+

(0+ )=

0+ i (t )d t =

0+ S

(t )d t + u

(0− )=

+ u

(0− ).

∫−

Следовательно, в этом случае uC (0+ ) ≠ uC (0− ).

Предположим к индуктивности приложена δ-функция напряжения uL (t ) = S0 δ0 (t ) ,

тогда при t = 0+

(0+ )=

0+ u

(t )d t =

0+ S

(t )d t + i

(0− )=

+ i

(0− ).

∫−

Следовательно, в этом случае iL (0+ ) ≠ iL (0− ). Таким образом, напряжение на емкости и ток через индуктивность могут быть разрывными.

Общий вывод: во всех случаях (изменение емкости и индуктивности, δ-функции токов и напряжений) начальные значения напряжений на емкостях и токи через индуктивности могут быть найдены. Это и есть правило коммутации в общей форме.

§6. Интеграл наложения (интеграл Дюамеля) через переходную и импульсную характеристику

Интеграл наложения — это математический аппарат, который позволяет по известной переходной или импульсной характеристике найти реакцию на любой произвольный сигнал.

Интеграл наложения через переходную характеристику

Пусть	для	произвольной	цепи известна	ее реакция	на входной сигнал
f (t ) = δ (t ) h (t ) ,		на вход цепи	действует сигнал	f (t ) = f + (t )	произвольной формы.
1	1

Необходимо найти реакцию цепи на такой сигнал, т. е. x(t ) . f (t )

f (0+ )

Воспользуемся единичной ступенчатой функцией для того, чтобы входной сигнал аппроксимировать прямыми.

f (t )

f (2 τ)

f ( τ)

0	τ	2 τ	t

f (t ) ≈ f (0+ )δ1 (t ) + ∑ f (n τ) δ1 (t − n τ)

n=1

Очевидно, что в силу линейности цепи реакция на воздействие f (t ) будет

x(t ) ≈ f (0+ )h1 (t ) + ∑ f (n τ) h1 (t − n τ)

n=1

f (t )

f (n

τ)

(

(n −1)

′[(

]

)

n − 1

f (t ) ≈ f (0+ )δ1 (t ) + ∑ f ′[(n − 1) τ] δ1 (t − n τ) τ

n=1

( )

≈ f

(

+ )

( )

∑ f

′[(

)

]

(

)

x t

− 1

h1 t − n

n=1

Перейдем к интегралу,

τ → d τ

τ → 0 :

(

+ )

( )

= f

δ1

( )

∫

′(

)

(

−

)

f t

δ1

x(t ) = f (0+ )h1 (t ) + ∫ f ′(τ) h1 (t − τ)d τ

(1)

Интеграл (1) называется интегралом наложения или интегралом Дюамеля.

( + )

( )

+ ∫ f

(

)

′

(

t −

)

d τ

(2)

x t

x(t ) = f (0+ )h1 (t ) + ∫ f ′(t − τ) h1 (τ)d τ

(3)

( + )

( )

+ ∫ f

(

t −

)

′(

)

d τ

(4)

x t

Примечание. Символом

′( )

′(

)

обозначены классические производные. Для

конкретных вычислений выбирают формулу (1–4), по которой проще считать.

Интеграл наложения через импульсную характеристику

Из связи между h1(t) и h0(t) имеем

(

)

(

+ )

( )

′(

)

= h1 0

δ0 t

+ h1

′(

)

= h0

(

)

− h1

(

+ )

δ0

(

)

(5)

Подставив (5) в (4) получим:

x(t ) = f (t ) h1 (0+ )+ ∫ f (t − τ)[h0 (τ) − h1 (0+ )δ0 (τ)]d τ = f (t ) h1 (0+ )+ ∫ f (t − τ) h0 (τ)d τ −

− ∫ f (t − τ) h1 (0+ )δ0 (τ)d τ = f (t ) h1 (0+ )+ ∫ f (t − τ) h0 (τ)d τ − f (t ) h1 (0+ ) = ∫ f (t − τ) h0 (τ)d τ

0 0 0

Итого получили:

t
x(t ) = ∫ f (t − τ) h0 (τ)d τ .	(6)
0

Примечание. Поскольку все формулы Дюамеля связаны с переходной или импульсной характеристиками, а они определены при нулевых предначальных условиях, то в тех случаях, когда предначальные условия ненулевые, их следует выделить в виде дополнительных зависимых источников. Затем вычислить реакцию цепи, во-первых, с помощью интеграла Дюамеля при нулевых предначальных условиях и, во-вторых, обычным образом, от выделенных зависимых источников. Далее пользуясь линейностью цепи сложить эти реакции.

§7. Анализ кусочно-линейной цепи в t-области

Анализ кусочно-линейной цепи отличается анализом переходных процессов при коммутации.

Анализ кусочно-линейной цепи сводится к n-кратному повторению анализа линейной цепи при переходе с одного участка линейности на другой с соответствующим изменением параметров цепи и предначальных условий.

Глава 3. Анализ пассивных и активных кусочно- линейных цепей в области комплексной переменной p =

σ + jω

§1. Преобразования Лапласа. Его основные свойства и теоремы

Пусть имеется функция f (t). Ее преобразованием Лапласа называется

∞

[ f (t)] = F ( p) = ∫ f (t)e − pt d t ,

где p = σ + jω — комплексная переменная, t > 0, f (t) < Mect , M ++ , c < σ .

Лапласов интеграл преобразует переменную t в переменную p. Основные свойства интеграла Лапласа:

1.[αf (t)] = α [ f (t)]

2.[ f (t) + g (t)]= [f (t)]+ [g (t)]

Основные теоремы:

1. D n f (t) ÷ p n F ( p) − p n−1 f (0− ) − p n−2 f ′(0− ) − ... − pf ( n−2) (0− ) − f ( n−1) (0− )

d n F ( p)

÷ (−t)n f (t)

d p

∞

F ( p)

∫

...∫ f (t) d t

0−

∞

f (t)

∫...∫F ( p) d p n ÷

t n

f (t ± τ)δ (t ± τ) ÷ F (P)e± pτ

F ( p m α) ÷ f (t)e± αt

f (αt) ÷

F1 ( p)F2 ( p) ÷ ∫ f1 (τ) f 2 (t − τ) d τ = ∫ f1 (t − τ) f 2 (τ) d τ

0−

9.f (0+ ) = lim pF ( p)

p→∞

10. f (∞) = lim pF ( p)

p→0

Отметим, что, как видно из теорем (1) и (3), операции дифференцирования и интегрирования алгебраизуются. Следовательно, если использовать преобразования Лапласа для решения линейных интегрально-дифференциальных уравнений, то эта задача алгебраизуется. Отметим, также, как видно из теоремы (9), начальное значение временной функции может быть вычислено по ее изображению, а из теоремы (1) видно, что надо знать предначальные условия, следовательно, при использовании операторного метода правило коммутации становится излишним.

Изображения некоторых функций:

[δ0 (t)] = 1

[δ−n ]= p n , n

[δ1 (t)]= 1 p

[e−αt ]=	1

	p + α
	p + α
[te−αt ]=	1

	( p + α)2
	( p + α)2
[cos(ωt)]=			ω

		p 2 + ω2
		p 2 + ω2
[sin(ωt)]=			p

			2 + ω2
		p	2 + ω2

§2. Постановка общей задачи анализа кусочно-линейных цепей в области комплексной переменной p = σ + jω. Вычисление обратного к преобразованию Лапласа с помощью теоремы Хевисайда

Общая задача анализа кусочно-линейных цепей в p-области

При переходе в p-область возможны следующие постановки задачи:

а) Можно преобразовать по Лапласу дифференциально-интегральные уравнения, описывающие динамику L- и C-элементов. На основании полученных

алгебраических уравнений построить операторную схему замещения этих элементов. Затем из них построить операторную схему замещения цепи и описать ее алгебраическими уравнениями Кирхгофа, относительно изображений искомых переменных. Далее решить эти уравнения относительно изображений.

б) Описать анализируемую цепь дифференциально-интегральными уравнениями Кирхгофа в t-области. С помощью теорем (1) и (3) преобразовать эти уравнения по Лапласу, получить в результате алгебраические уравнения относительно изображений искомых переменных и затем решить их.

в) Описать исследуемую цепь в t-области уравнениями состояния, преобразовать их по Лапласу и полученные алгебраические уравнения, относительно изображений искомых переменных, решить обычным образом.

Вычисление обратного преобразования Лапласа с помощью т. Хевисайда

В силу того, что формула Лапласа

∞

x(t ) =

∫ F ( p)e pt dp

j 2π

−∞

практически непригодна для поиска обратного преобразования, рассмотрим

вычисление функции x(t), как это было предложено Хевисайдом.

Решив систему уравнений относительно X ( p) , получим:

′

m−1

′

X ( p) =

B ( p)

bm p

+ bm−1 p

+ ... + b1 p + b0

, где m ≥ n , m = n

+ J .

A( p)

p n

+ a

n−1

p n−1 + ... + a p + a

Вспомним, что:

− J

x(t) = x − (t) + x + (t) = ∑S j δj + x + (t) .

j =0

Следовательно:

X ( p) = X − ( p) + X + ( p) , где X − ( p) - изображение сингулярной составляющей,

X + ( p) - изображение регулярной составляющей.

	′	( p)	− J		B( p)

X ( p) =	B		= ∑S j	p − j +		, где deg( A) ≥ deg(B) .

	A( p) j =0				A( p)

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20163.59 Mб6Lecture_01.pdf
#
22.03.20163.16 Mб8Lecture_06.pdf
#
22.03.20162.32 Mб9Lecture_09.pdf
#
22.03.20163.22 Mб6Lecture_10.pdf
#
22.03.20163.08 Mб8Lecture_11_1.pdf
#
09.02.2015524.26 Кб13lekcii toe.pdf
#
20.09.2019140.29 Кб2LEKCYA_2.DOC
#
21.11.2019769.54 Кб73Lektsia_RBU-1.doc
#
21.11.2019174.08 Кб27Lektsia_RBU-3.doc
#
22.11.20191.01 Mб38Lektsii_4_semestr.docx
#
15.04.201941.52 Mб4Lektsii_po_metrologii.doc