§7. Аналитическая геометрия в пространстве
7.1. Уравнение плоскости в пространстве
Рассмотрим трехмерное пространство с заданной декартовой системой координат.
Общее уравнение плоскости
У
тверждение.
Любая плоскость в трехмерном пространстве
описывается уравнением первого порядка:
Ах+Ву+Cz+D=0
(A2+B2+C20)
В
частности, если D=0,
то плоскость проходит через начало
координат; плоскость хОу
имеет уравнение z=0;
плоскость xOz
имеет уравнение y=0;
плоскость yOz
имеет уравнение х=0.
Нормальное уравнение плоскости
Пусть
известна точка М0(х0;у0;z0),
принадлежащая плоскости (начальная
точка) и
ненулевой вектор
,
перпендикулярный этой плоскости (его
называют нормальным
вектором плоскости).
Произвольная
точка пространства М(х;
у;
z)
принадлежит данной плоскости тогда и
только тогда, когда
,
то есть
.
Записывая скалярное произведение в
координатной форме, получаем нормальное
уравнение плоскости:
Если в этом уравнении раскрыть скобки, получится общее уравнение плоскости: Ах+Ву+Cz+D=0 (где D=-Ax0-By0-Cz0). Этот факт и доказывает сформулированное выше утверждение.
Уравнение плоскости по трем точкам
Пусть даны три точки, принадлежащие плоскости: М1(х1;у1;z1), M2(x2;y2;z2), M3(x3;y3;z3).
Произвольная
точка пространства М(х;
у;
z)
принадлежит данной плоскости тогда и
только тогда, когда векторы
компланарны, то есть их смешанное
произведение равно нулю. Таким образом,
получаем уравнение данной плоскости в
виде:
;
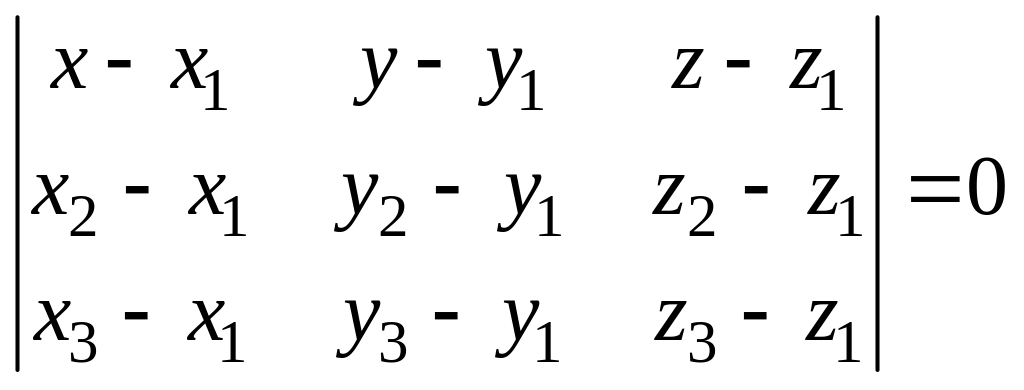раскрыв определитель по первой строке, получаем общее уравнение плоскости.
Аналогично,
если дана точка М0(х0;у0;z0),
принадлежащая плоскости (начальная
точка) и
два вектора
,
параллельные этой плоскости, то уравнение
плоскости записывают в виде
7.2. Уравнения прямой в пространстве
О
бщее
уравнение прямой
Пусть
прямая задана как пересечение двух
плоскостей:
,
где
,
.
Тогда
система
задает множество точек прямой и
называется общим уравнением прямой.
К анонические уравнения прямой
Пусть
задана начальная точка прямой Р0(х0,
y0,
z0)l
и направляющий вектор
.
Т
огда
,
откуда получаем уравнения прямой в виде
.
Аналогичным
образом составляются канонические
уравнения прямой, проходящей через две
данные точки Р1
и Р2,
так что в качестве направляющего вектора
можно выбрать вектор
.
Параметрические уравнения прямой
В
ведение
коэффициента пропорциональности t
в канонические уравнения прямой позволяет
записать ее параметрические уравнения:
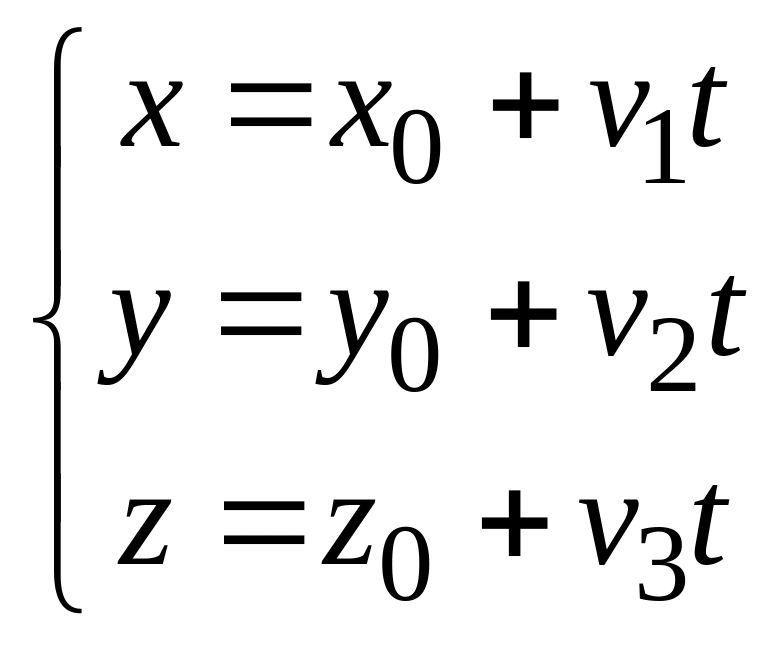
Эти уравнения означают, что для каждой точки прямой существует значение параметра t через который выражаются координаты этой точки и наоборот, для каждого значения t точка с соответствующими координатами принадлежит прямой.
Применение этих уравнений удобно, например, для нахождения точки пересечения прямой и плоскости.
7.3. Взаимное расположение прямых и плоскостей
Пусть прямые и плоскости заданы своими уравнениями:
, ,
,
.
Заметим,
что эти уравнения позволяют нам выписать
нормальные векторы данных плоскостей:
,
направляющие векторы прямых:
и начальные точки прямых:
.
Тогда:
а)
;
б)
;
в)
углом между плоскостями называется
острый угол между их нормальными
векторами:
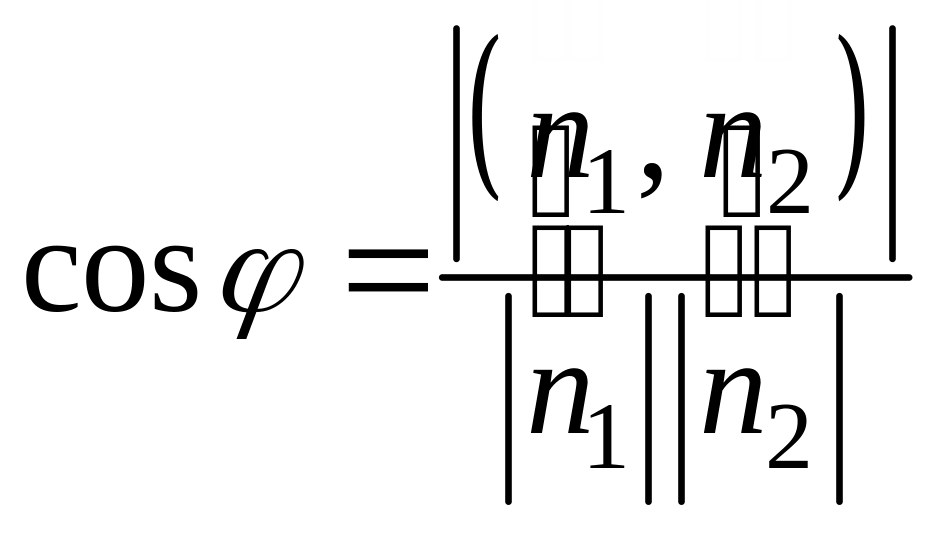
г)
(в
частности, может быть
);
д)
;
е
)
(в
частности, может быть
);
ж)
компланарны
;
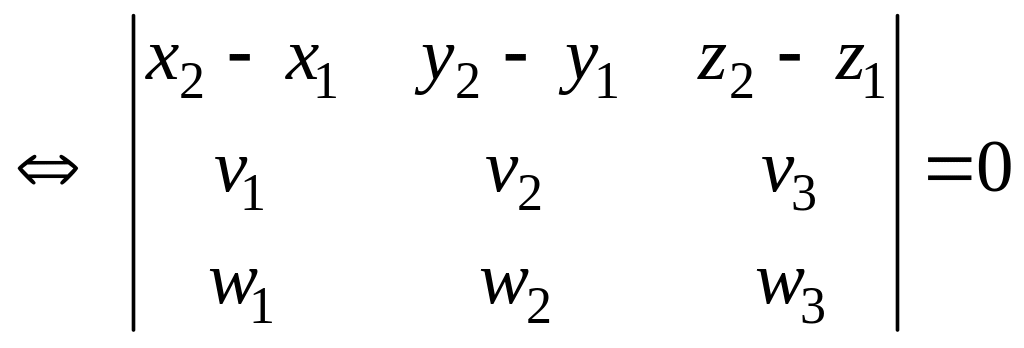з
)
углом между прямыми называется острый
угол между их направляющими векторами:
;
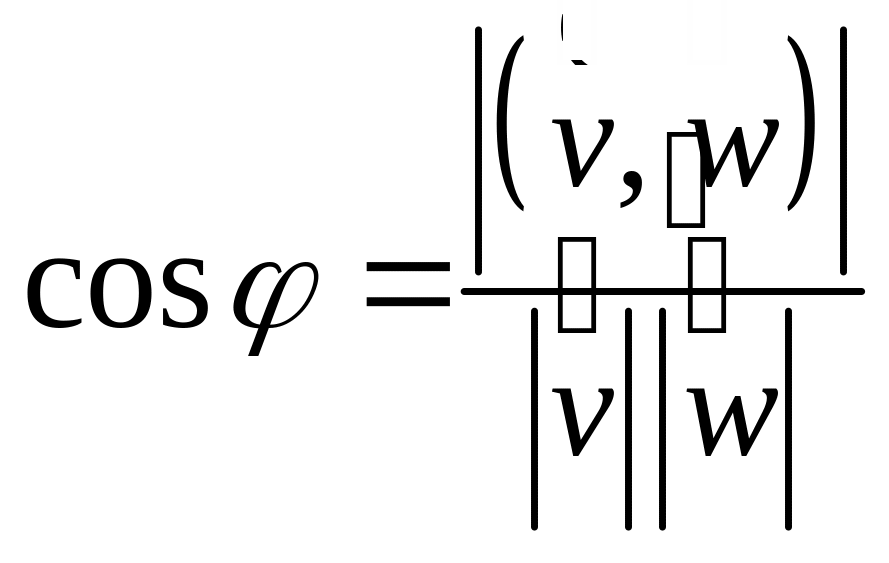и) угол между прямой l1 и плоскостью 1 равен углу между прямой и ее проекцией на плоскость, но удобнее его находить при помощи угла между прямой и перпендикуляром к плоскости:
.
Пример. Найти точку Q, симметричную точке P(10; -5; 6) относительно плоскости , в которой лежат прямые
Решение:
Прежде всего, найдем уравнение плоскости
.
Эта плоскость проходит через точку
М1(-1;
3; 2) параллельно двум векторам
и
,
следовательно, ее уравнение имеет вид:
.
Раскрыв определитель по первой строке, получаем:
,
далее, сократим на 4 и раскроем скобки:
.
Для того, чтобы найти точку, симметричную данной относительно плоскости, необходимо опустить из точки Р на плоскость перпендикуляр l, затем найти точку N пересечения полученной прямой и плоскости и отложить на этой прямой отрезок NQ, равный от резку PN.
Поскольку
,
то в качестве направляющего вектора
прямой мы можем выбрать нормальный
вектор плоскости, координаты которого
находятся из уравнения плоскости:
.
Следовательно, уравнение перпендикуляра:
.
Чтобы
найти точку пересечения прямой и
плоскости
,
запишем уравнения прямой l
в параметрической форме и подставим в
уравнение плоскости :
;
.
Таким образом, координаты точки N:
.
Далее,
точка N
является серединой отрезка PQ,
следовательно,
,
аналогично
.
Таким образом, Q(-14; 7; -2).