
- •Тема I – линейная алгебра
- •§1. Матрицы и действия над ними
- •1.1. Основные понятия
- •1.2. Действия над матрицами
- •§2. Определители
- •2.1. Основные понятия
- •2.2. Свойства определителей
- •§3. Обратная матрица
- •3.1. Основные понятия
- •3.2. Решение матричных уравнений
- •3.3. Метод элементарных преобразований
- •§4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия
- •4.2. Правило Крамера решения слау
- •4.3. Метод Гаусса решения слау
- •§5. Векторы
- •5.1. Основные понятия
- •Для того, чтобы задать вектор, необходимо указать:
- •5.2. Операции над векторами
- •5 .3. Координаты векторов
- •5 .4. Скалярное произведение векторов
- •5.5. Векторное произведение
- •5.6. Смешанное произведение
- •§6. Аналитическая геометрия на плоскости
- •6.1. Уравнения прямых на плоскости
- •6.2. Кривые второго порядка на плоскости
- •§7. Аналитическая геометрия в пространстве
- •7.1. Уравнение плоскости в пространстве
- •7.2. Уравнения прямой в пространстве
- •7.3. Взаимное расположение прямых и плоскостей
- •7.4. Поверхности второго порядка
5 .4. Скалярное произведение векторов
Скалярным произведением двух векторов
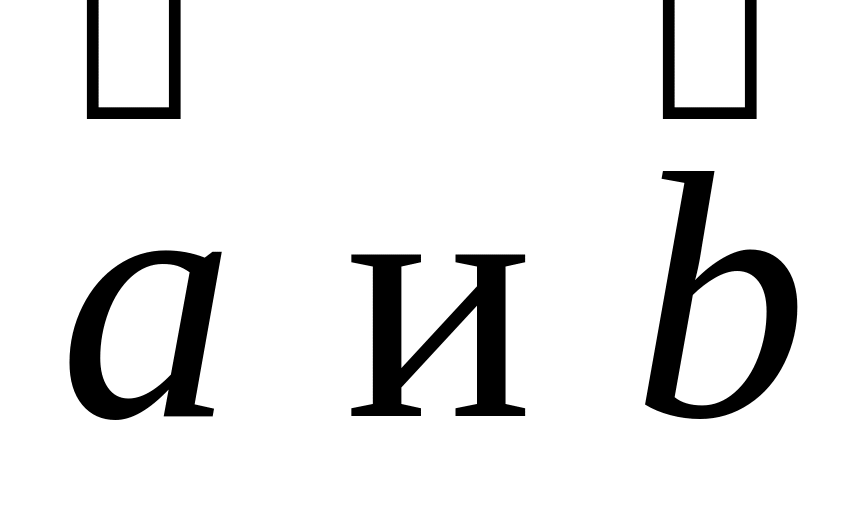 называется число
называется число
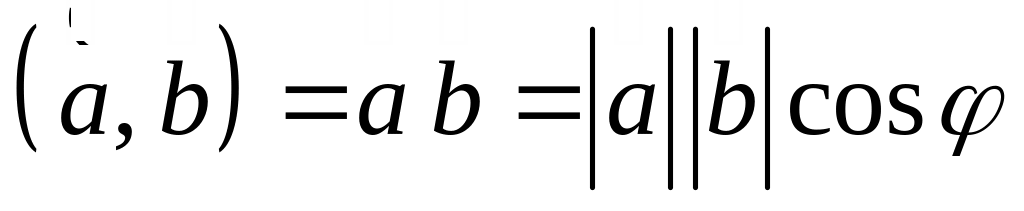
(где - угол между векторами , отложенными из одной точки).
Свойства:
1)
![]() для любых векторов
для любых векторов
![]()
2)
![]() для любых векторов
и числа
для любых векторов
и числа
3)
![]() для любых векторов
для любых векторов
![]()
4)
![]()
5)
![]() (при этом считается, что нулевой вектор
перпендикулярен любому)
(при этом считается, что нулевой вектор
перпендикулярен любому)
6)
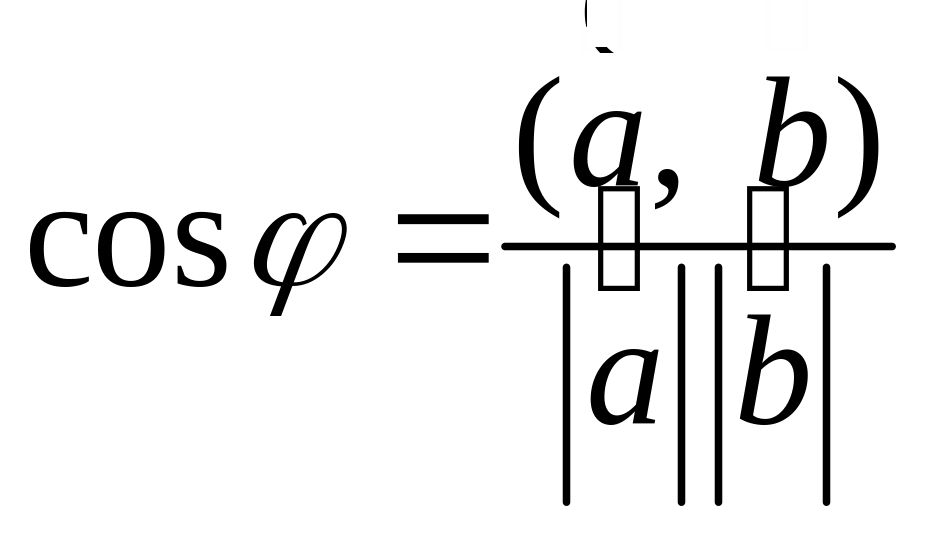 .
.
Теорема 5.3. Пусть , . Тогда
![]() .
.
Доказательство: Воспользуемся разложением векторов по базису и свойствами скалярного произведения:
![]()
![]()
![]() .
.
Последнее равенство следует из того, что
![]()
 (т.к.
(т.к.
![]() )
и т.п.
)
и т.п.
Следствие.
![]() .
.
Замечание. Для векторов на плоскости, соответственно,
![]() и
и
![]() .
.
Пример 1. Найти угол между векторами
![]()
Решение:
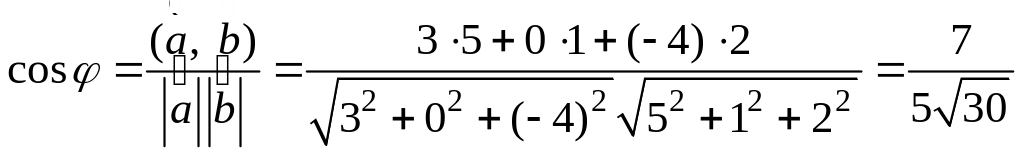 ,
,
![]() .
.
Пример
2.
![]() .
.
Найти
![]() .
.
Решение: Используем свойства скалярного произведения:
![]()
![]() .
.
Пример. Даны точки: А(-2; 1), В(3; 0), С(1; 4). Найти основание высоты треугольника АВС, проведенной из точки В.
Р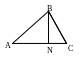 ешение:
Точка N(xN,
yN)
АС
ешение:
Точка N(xN,
yN)
АС
![]()
![]()
![]() ;
;
BN
– высота треугольника, то есть
![]()
![]()
![]() .
.
Получили два линейных уравнения относительно координат:
![]()
![]() .
.
Таким образом, искомая точка N(0; 3).
5.5. Векторное произведение
В
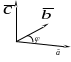 екторным
произведением
двух векторов
называется вектор
екторным
произведением
двух векторов
называется вектор
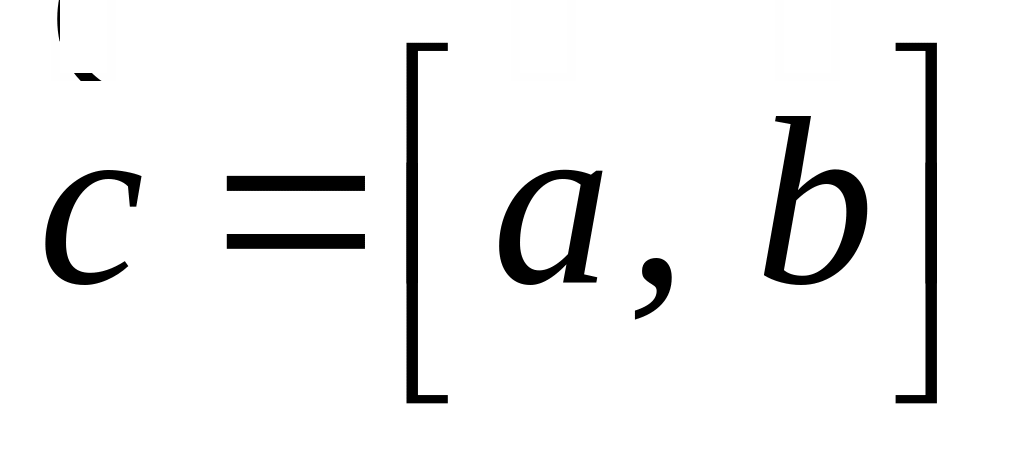 ,
определяемый следующим образом:
,
определяемый следующим образом:
1)
![]() ,
где
- угол между векторами
,
где
- угол между векторами
2)
![]()
3)
векторы
![]() образуют правую тройку векторов.
образуют правую тройку векторов.
Свойства:
1)
![]() (антикоммутативность);
(антикоммутативность);
2)
![]() ;
;
3)
![]()
4)
![]()
![]()
5) (геометрический смысл векторного произведения):
м одуль
векторного произведения равен площади
параллелограмма, построенного на
векторах
:
одуль
векторного произведения равен площади
параллелограмма, построенного на
векторах
:
![]()
Теорема
5.4.
Пусть
,
![]() .
Тогда
.
Тогда
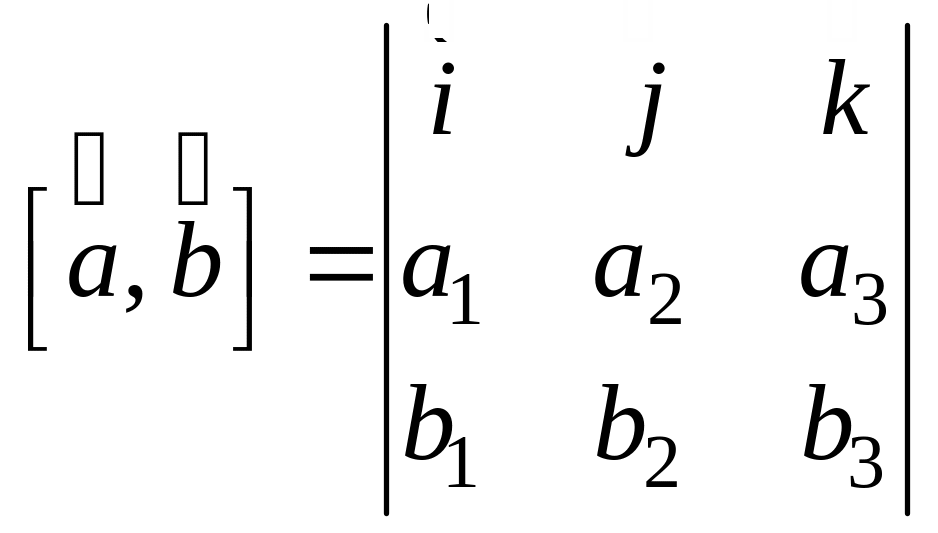
Доказательство аналогично доказательству соответствующей теоремы о скалярном произведении, с поправкой на свойства векторного произведения.
Замечание. Для векторов на плоскости (с двумя координатами) векторное произведение не определено.
Пример.
Даны векторы:
![]() .
Найти высоту параллелограмма, построенного
на этих векторах, опущенную из конца
вектора
.
.
Найти высоту параллелограмма, построенного
на этих векторах, опущенную из конца
вектора
.
Р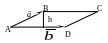 ешение:
ешение:
Рассмотрим параллелограмм ABCD, построенный на данных векторах. С одной стороны, как известно,
![]() .
.
С
другой стороны, воспользовавшись
геометрическим смыслом векторного
произведения, имеем:
![]() .
.
Найдем векторное произведение:
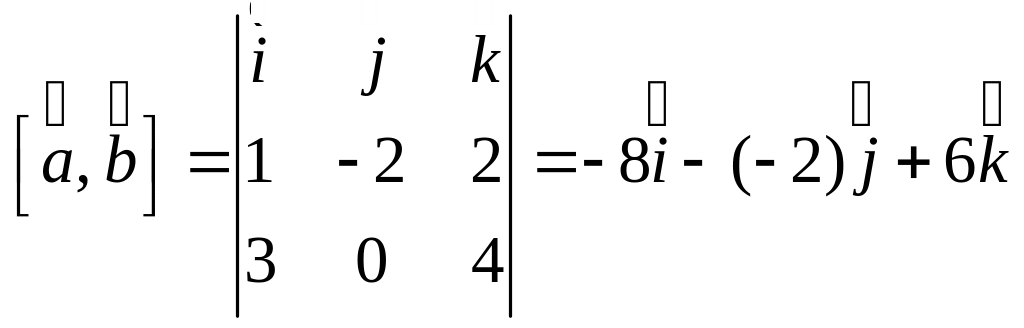 ,
,
следовательно,
![]() .
.
Кроме
того, найдем
![]()
Таким
образом,
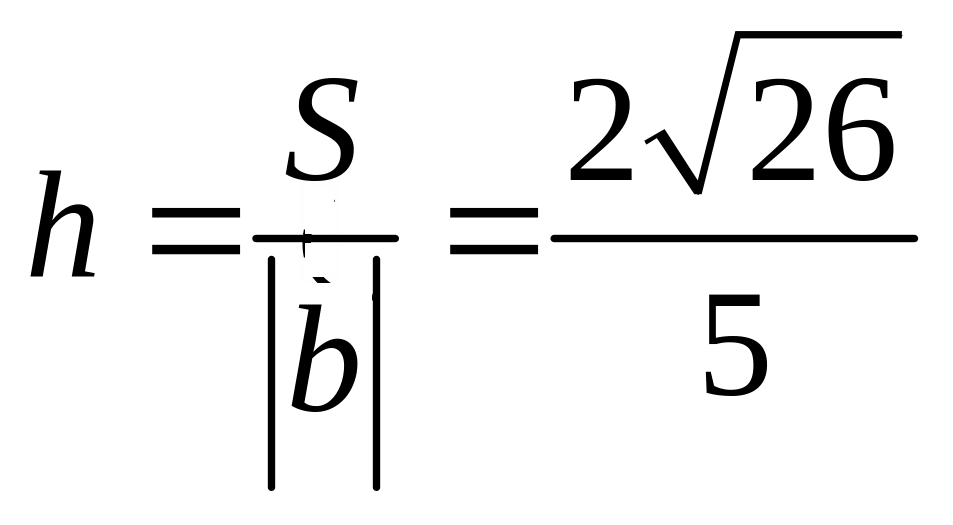 .
.
5.6. Смешанное произведение
Смешанным произведением трех векторов
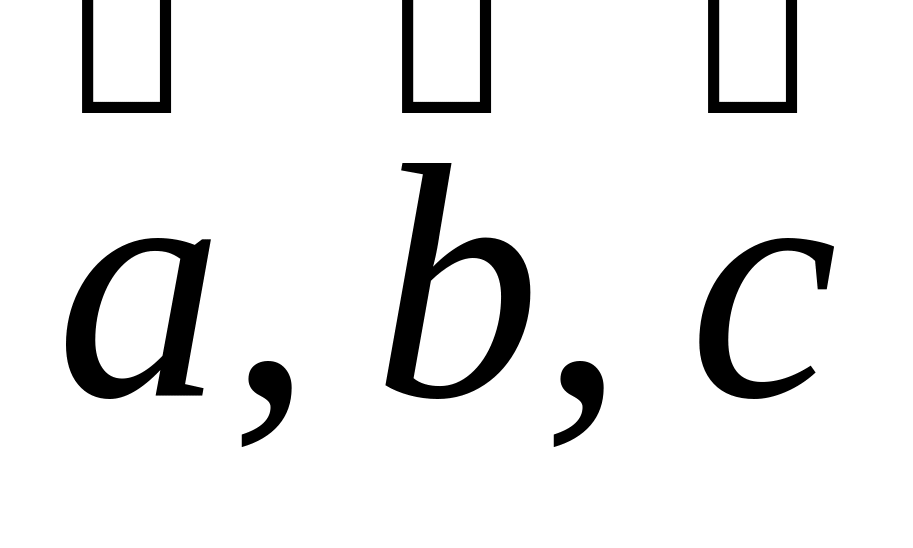 называется число, определяемое
соотношением
называется число, определяемое
соотношением
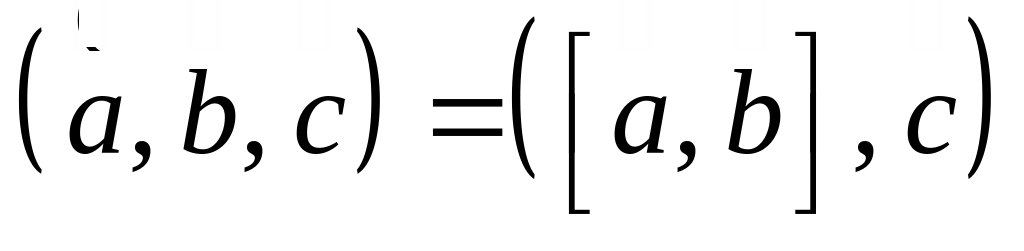 .
.
Из свойств смешанного произведения особый интерес на практике представляет его геометрический смысл:
Т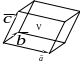 еорема
5.5. Модуль
смешанного произведения трех ненулевых
векторов
равен объему
параллелепипеда, построенного на этих
векторах, отложенных из одной точки:
еорема
5.5. Модуль
смешанного произведения трех ненулевых
векторов
равен объему
параллелепипеда, построенного на этих
векторах, отложенных из одной точки:
![]() .
.
Следствие. Три ненулевых вектора компланарны тогда и только тогда, когда их смешанное произведение равно 0.
Из определения смешанного произведения и теорем о вычислении скалярного и векторного произведений следует следующая теорема:
Теорема
5.6. Пусть
,
б
![]() .
Тогда
.
Тогда
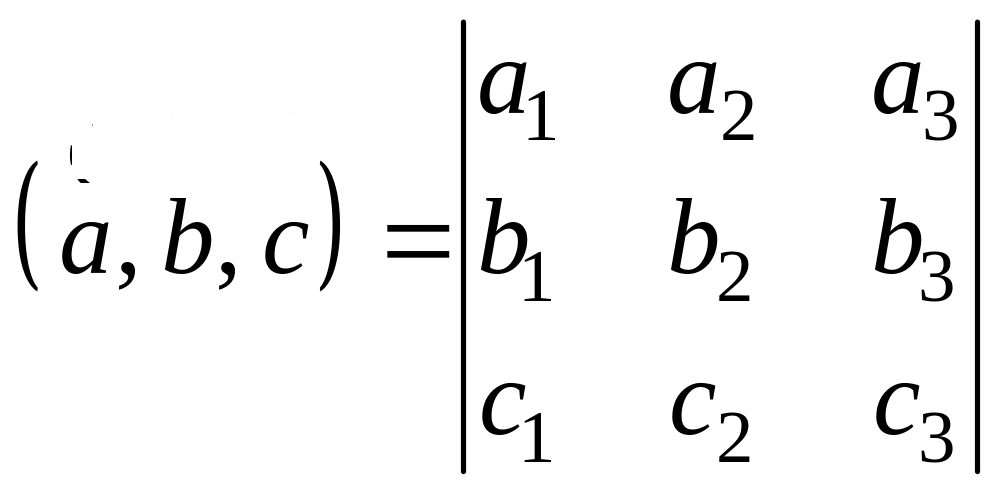 .
.
Пример. Выяснить, лежат ли точки A(5; 7; -2), B(3; 1; -1),
C(9; 4; -4), D(1; 5; 0) в одной плоскости.
Решение:
Данные точки будут лежать в одной
плоскости в том и только том случае,
если векторы
![]() компланарны, что в свою очередь,
равносильно утверждению, что смешанное
произведение этих векторов равно 0.
Проверим, так ли это.
компланарны, что в свою очередь,
равносильно утверждению, что смешанное
произведение этих векторов равно 0.
Проверим, так ли это.
![]() ;
;
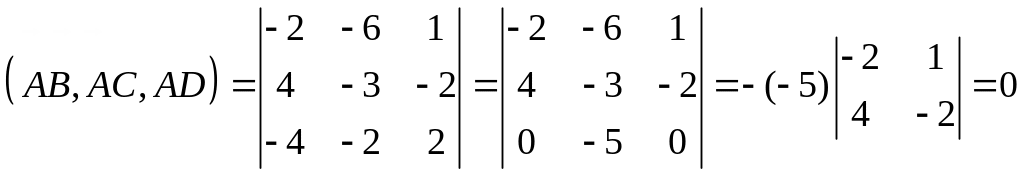 ,
,
следовательно, данные точки лежат в одной плоскости.
