§3. Обратная матрица

3.1. Основные понятия

• Квадратная матрица А^-1 называется обратной к квадратной матрице А того же порядка, если имеет место соотношение .

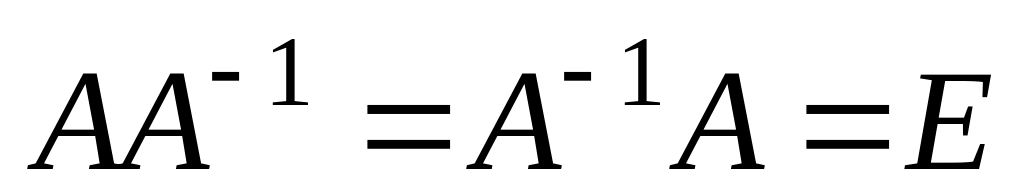Теорема 3.1. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной. При этом обратная матрица определяется формулой:

,

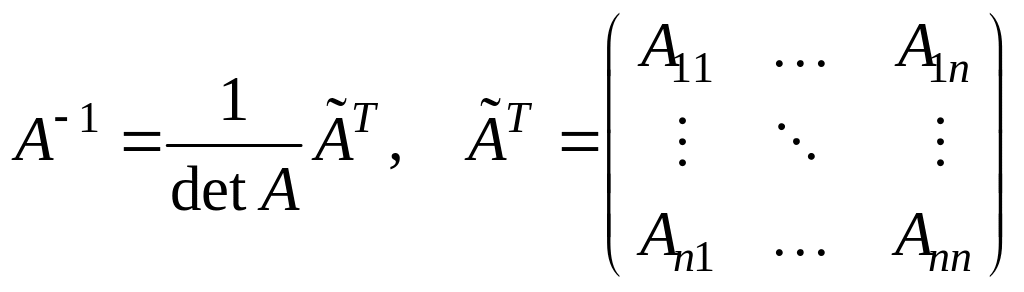где A_ij – алгебраические дополнения к элементам а_ij матрицы А^Т.

• Матрица называется присоединенной для матрицы А.

Пример. Найти обратную матрицу для матрицы .

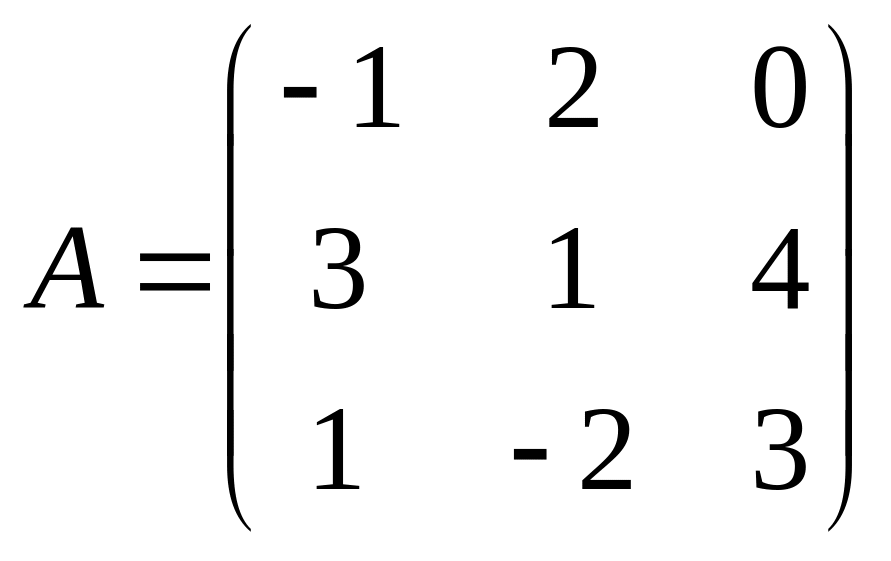Решение.

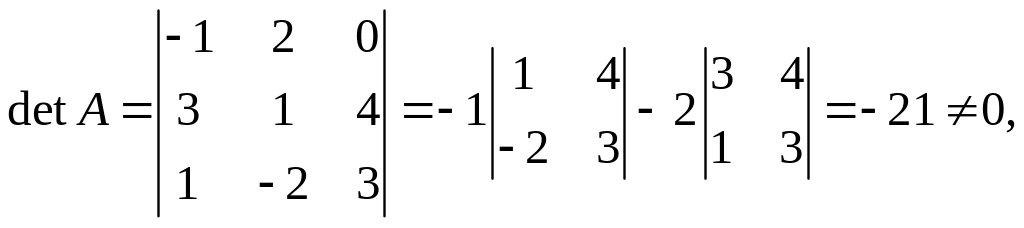
следовательно, обратная матрица существует. Для ее нахождения запишем матрицу А^Т вычислим алгебраические дополнения к ее элементам:

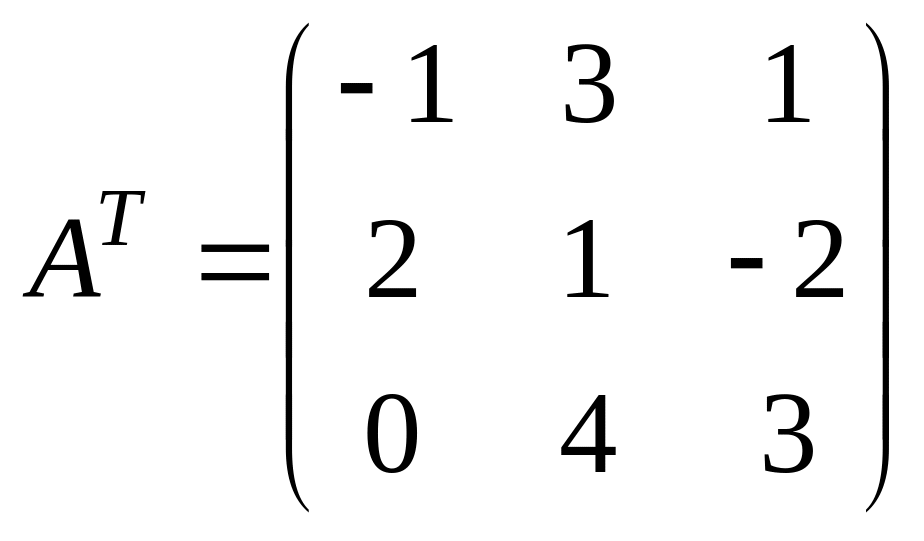
Таким образом, .

Проверим, является ли найденная матрица действительно обратной для данной матрицы А:

Следовательно, обратная матрица найдена верно.

3.2. Решение матричных уравнений

Рассмотрим матричное уравнение:

АХ=В

Пусть А – квадратная невырожденная матрица. Тогда, согласно приведенной выше теореме, существует обратная матрица А^-1. Умножим обе части данного уравнения на А^-1 слева (напомним, что произведение матриц не является коммутативной операцией!):

А^-1АХ=А^-1В  ЕХ=А^-1В  Х=А^-1В – решение данного матричного уравнения.

Аналогично, уравнение ХА=В, где А – квадратная невырожденная матрица, имеет решение Х=ВА^-1 (умножаем обе части уравнения на А^-1 справа).

Пример. Решить матричное уравнение ,

где

Решение:

.

Проверка: .

3.3. Метод элементарных преобразований

• Элементарными преобразованиями строк матрицы А называются:

  • умножение одной строки матрицы на число, отличное от 0;

  • перемена мест строк;

  • сложение строк

  • прибавление к одной строке другой строки, умноженной на число.

1) Для того, чтобы по заданной матрице А найти обратную, следует записать так называемую расширенную матрицу:

и при помощи элементарных преобразований строк привести ее к виду

.

2) Для того, чтобы решить матричное уравнение АХ=В, с квадратной невырожденной матрицей А, следует записать расширенную матрицу

и при помощи элементарных преобразований строк привести ее к виду

.

3) Для того, чтобы решить матричное уравнение ХА=В, с квадратной невырожденной матрицей А, следует прежде всего транспонировать это уравнение: А^ТХ^Т=В^Т и при помощи элементарных преобразований строк расширенной матрицы привести ее к виду , после чего транспонировать полученную матрицу Х^Т.

Пример: Найти обратную матрицу для матрицы .

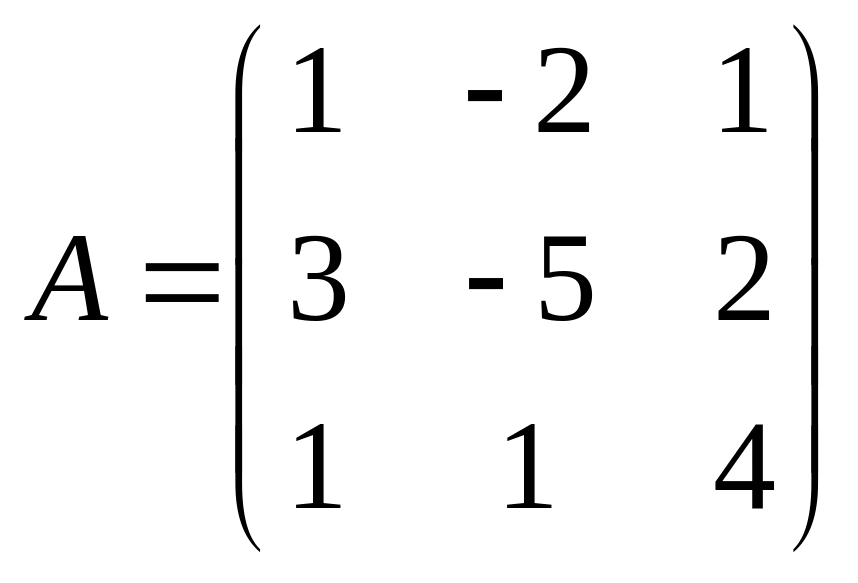Решение:

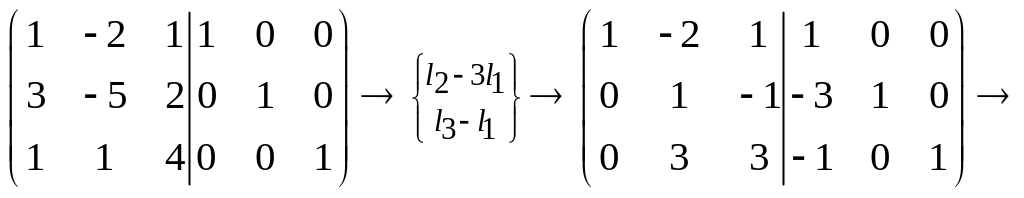
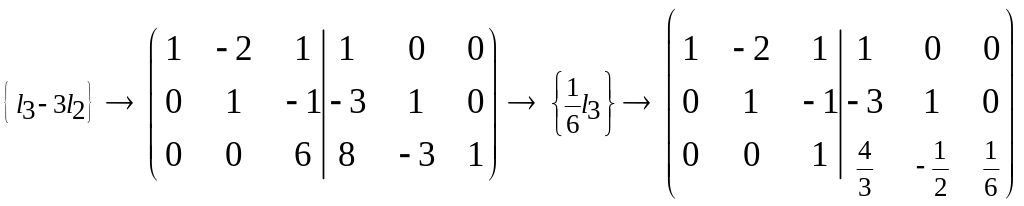
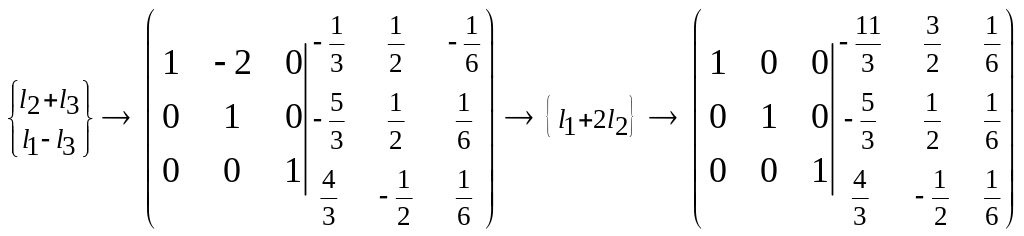
Таким образом, .

§4. Системы линейных алгебраических уравнений

4.1. Основные понятия

Рассмотрим систему m линейных алгебраических уравнений (СЛАУ) с n неизвестными:

(1)

Напомним некоторые определения:

• СЛАУ называется однородной, если все свободные коэффициенты равны 0: ;

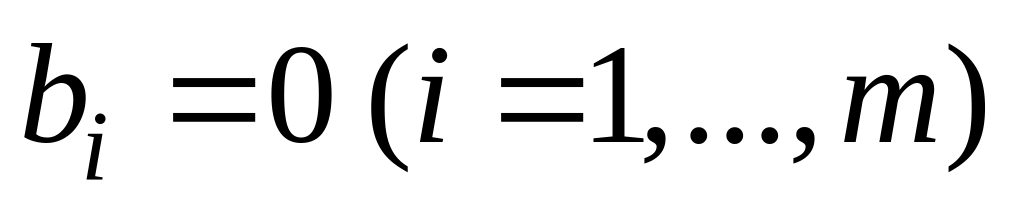• Решением СЛАУ называется упорядоченный набор чисел х₁,…,х_n таких, что при их подстановке в уравнения системы последние обращаются в верные тождества;

• СЛАУ называется совместной, если она имеет решение и несовместной в противном случае.

Рассмотрим теперь матричное уравнение

, (2)

где .

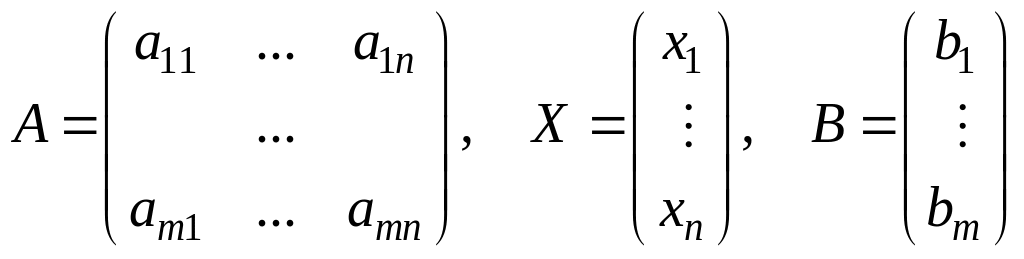Из определений умножения и равенства матриц следует, что матричное уравнение (2) эквивалентно СЛАУ (1).

• Матрица А называется матрицей системы (1), матрица-столбец Х – столбцом неизвестных, а матрица-столбец В – столбцом свободных коэффициентов. СЛАУ (1) называется квадратной, если матрица А квадратная (то есть число уравнений системы равно числу неизвестных), вырожденной если матрица А вырожденная и невырожденной в противном случае. Определитель матрицы А называется определителем системы (1).

Таким образом, если дана квадратная невырожденная СЛАУ, то, записав ее в матричной форме, мы можем воспользоваться методами решения матричных уравнений.

Пример 1: Записать матричное уравнение АХ=В в виде системы линейных уравнений: и выяснить, является ли тройка чисел (2; 1; 4) ее решением.

Решение: Поскольку произведение матрицы А размера 33 на столбец неизвестных должно быть равно столбцу свободных членов размера 31,

следовательно, столбец неизвестных также имеет размер 31: .

Составим произведение АХ и приравняем его к В:

таким образом, получаем СЛАУ:

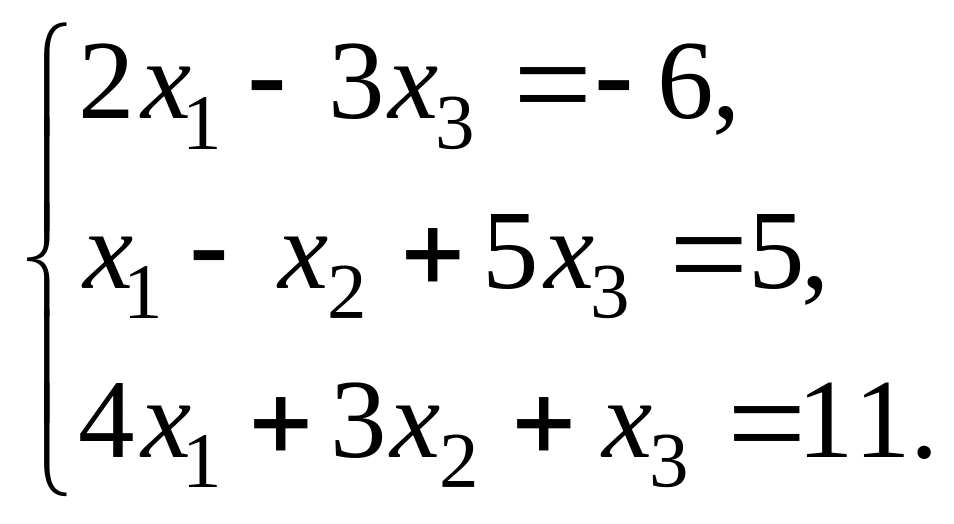
Проверим, является ли данная тройка чисел решением этой системы. Для этого подставим эти числа вместо неизвестных в уравнения системы.

Из первого уравнения получаем: 22+01-34=-6 – верное равенство,

из второго уравнения получаем: 2-1+54=5 – неверное равенство,

следовательно, данная тройка чисел не является решением системы.

Пример 2. Решить систему линейных уравнений

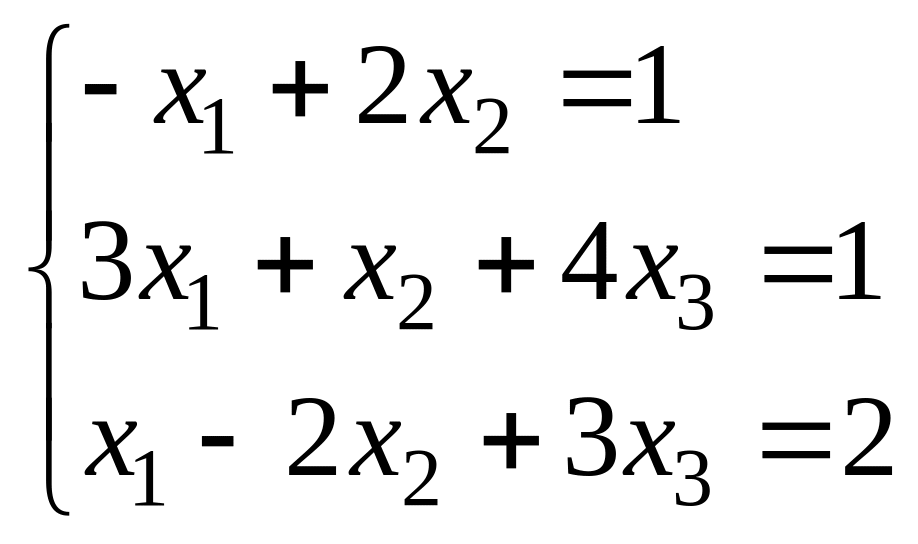
Решение:

Для матрицы системы мы уже находили ранее обратную матрицу: 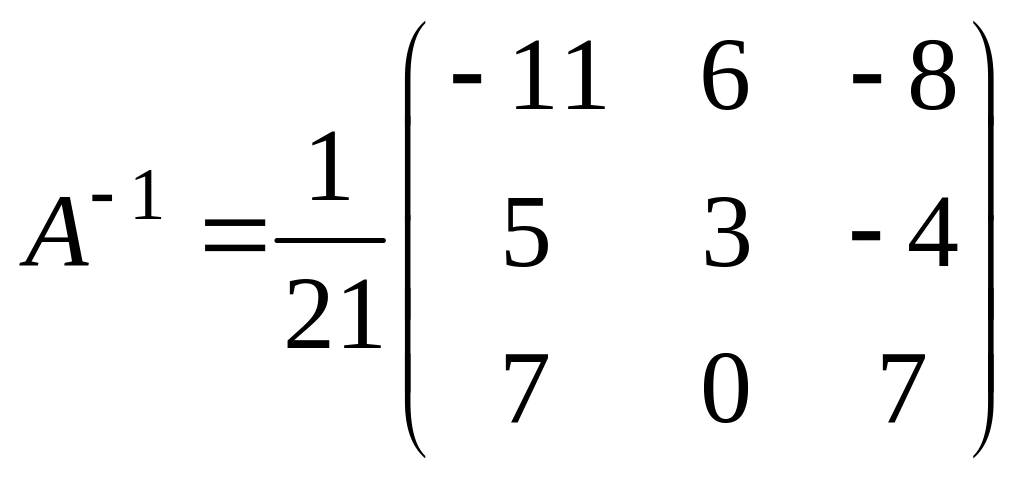. Следовательно,

Непосредственной проверкой можно убедиться, что (-1; 0; 1) действительно является решением данной системы.