Блок информации

Сглаживание экспериментальных зависимостей можно выполнять методом наименьших квадратов. Уравнение регрессии может быть линейным, квадратичным и др. Рассмотрим простейший случай зависимости y=kx+b. Часто требуется построение графиков по эмпирическим данным или экспериментальное подтверждение известным из теории функциональным зависимостям между физическими величинами. Например, известна зависимость сопротивления металлов от температуры

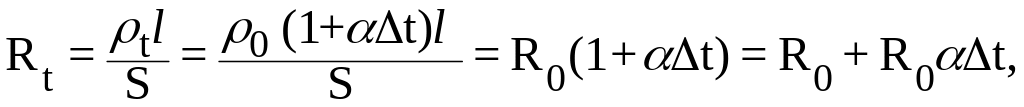(10.1)

которую можно записать в виде линейной зависимости

y=ax+b, (10.2)

где у=R_t, x=t, b=R_o, a=R_o. Часто популяционный рост на небольших участках времени также аппроксимирует такой линейной зависимосьтью.

В общем случае экспериментальных измерениях получают множество x_i и соответствующих им y_i (в данном случае t_i и R_ti). Однако, существуют случайные отклонения (ошибки) и, как следствие, разброс точек, т.е. вместо гладкой линии получается ломаная кривая. Для усреднения эмпирических зависимостей и получения наиболее реального графика используют графический, арифметический, алгебраический способы выравнивания экспериментальных данных. Наиболее точный из них- алгебраический, метод наименьших квадратов. В этом случае составляют сумму квадратов отклонений эмпирических значений y_i от предполагаемых теоретических f(x_i) и требуют минимума этой суммы, т.е.

(10.3)

где Wmin, n- число измерений

При этом отдельные точки могут значительно отклоняться от графика (см. рис. 10.1), но, в целом, вся совокупность точек отклоняется на минимальное расстояние.

Так как в функцию f(x) входят параметры a,b, .., т.е. f(x,a,b...), то минимизируют по параметрам, используя необходимое условие экстремума функции W=W(a, b):

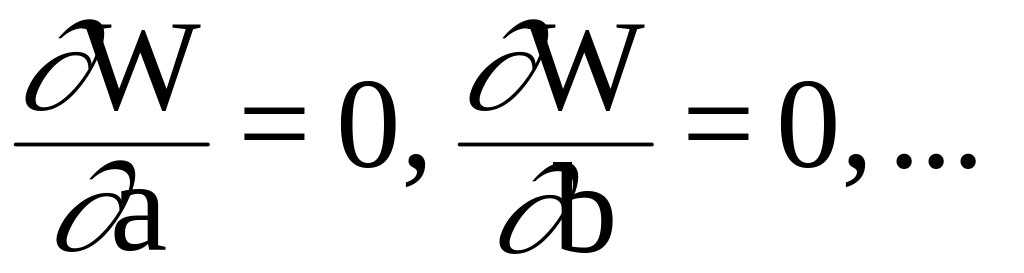(10.4)

Поясним выше сказанное на конкретном примере зависимости (10.2). Здесь после подстановки f(x) имеем:

,

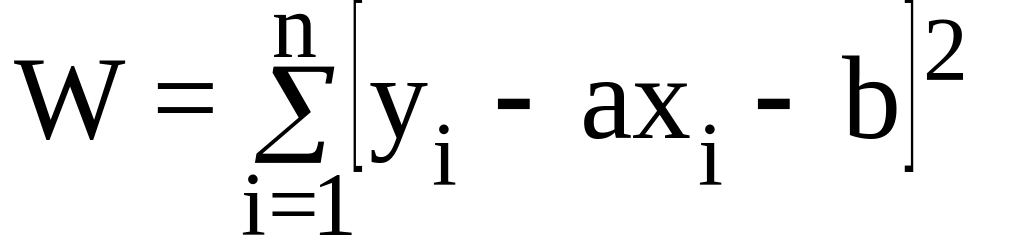тогда

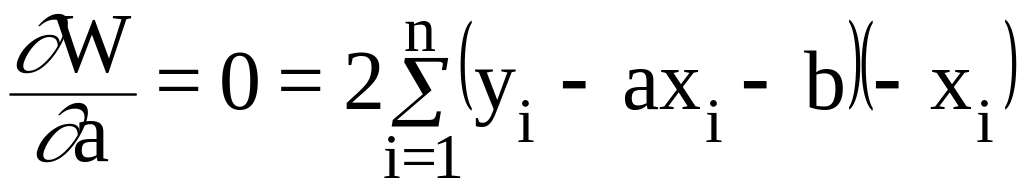
или

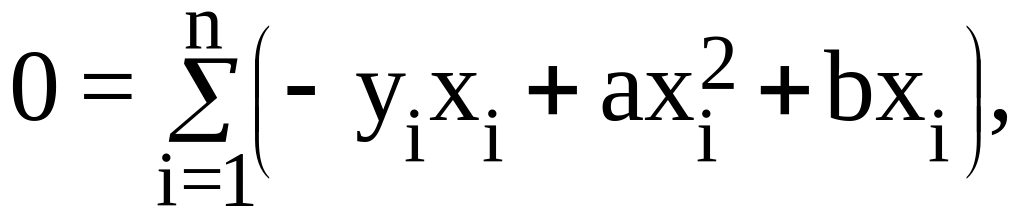(10.5)

а

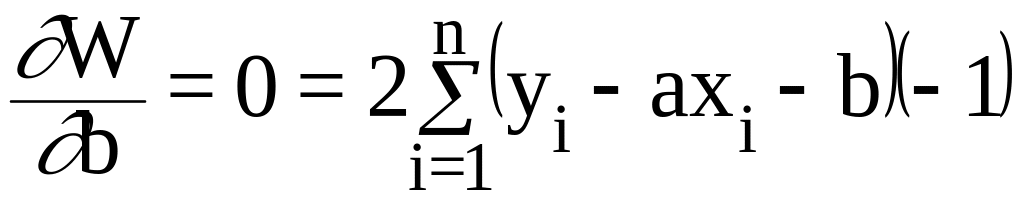
или

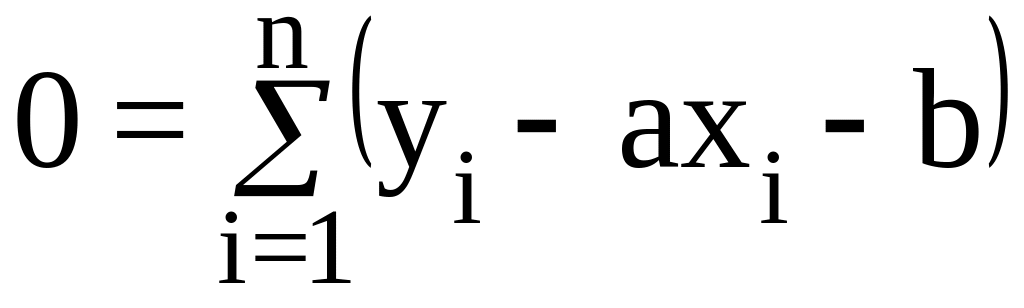(10.6)

Получим систему двух уравнений (10.5)и (10.6) относительно неизвестных a и b (y_i,x_i получены в эксперименте). Эта система имеет вид:

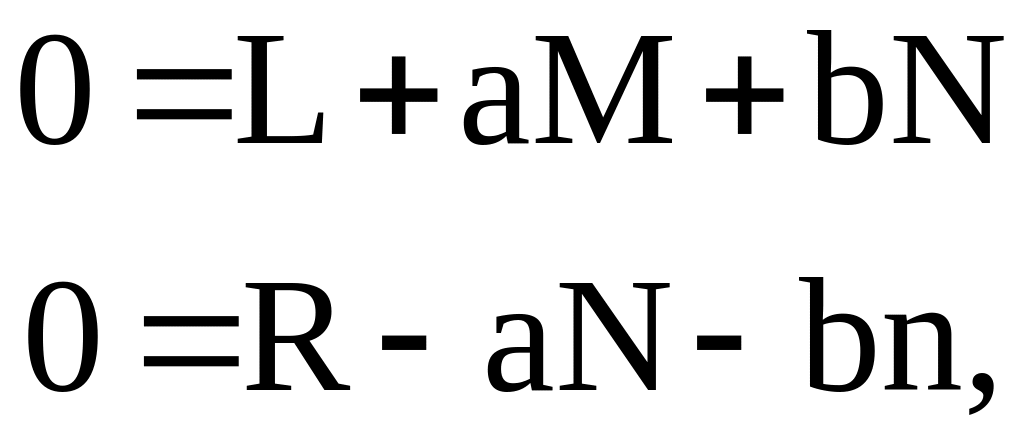
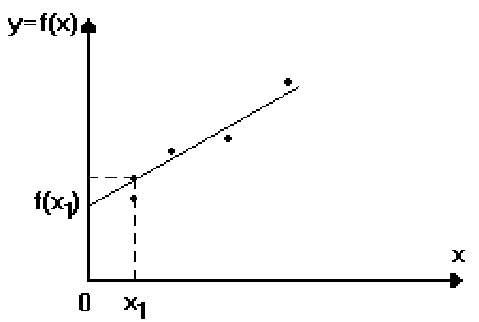
Рис.10.1. Реализация метода наименьших квадратов

где

.

Тогда получим

Из решения этой системы уравнений можно получить для примера (10.1) значения параметров R₀ и a:

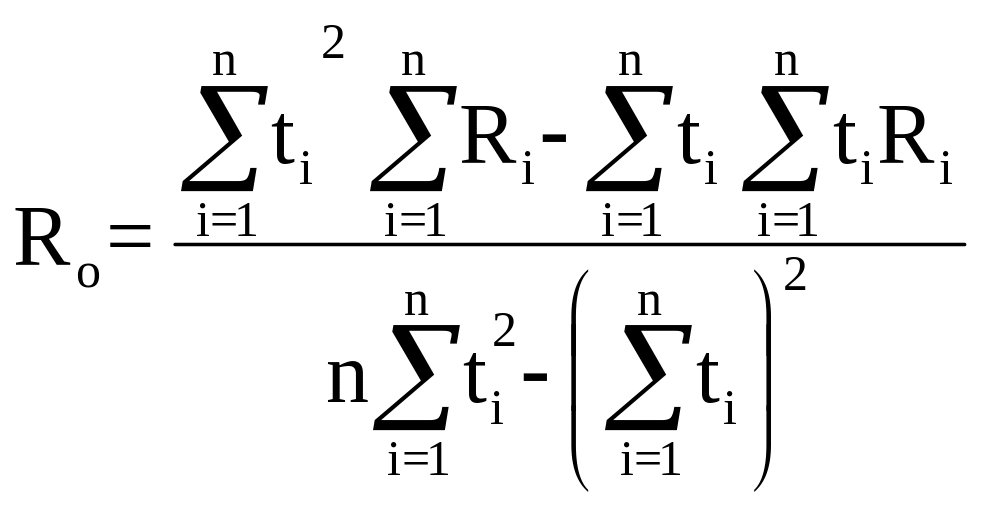(10.7)

и температурный коэффициент

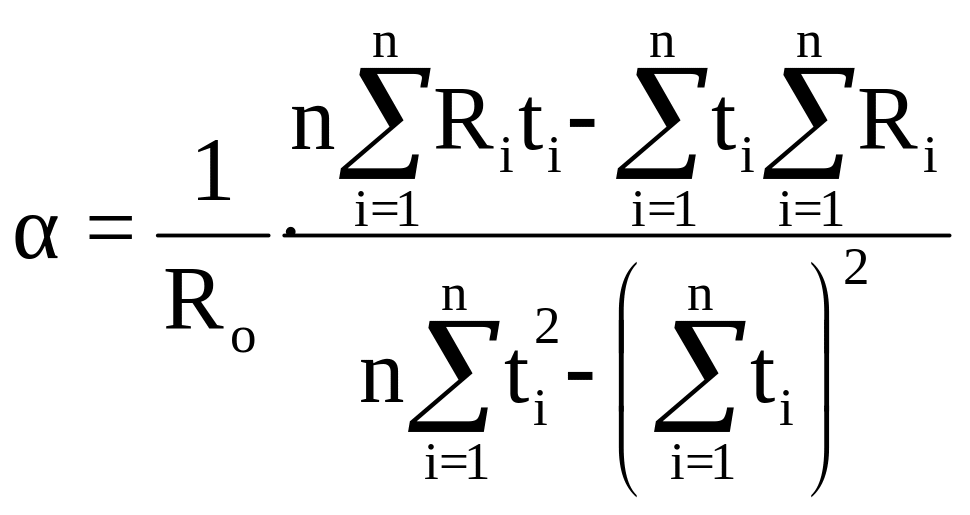(10.8)

Зная R_o и  легко построить график зависимости R=R(t). Отметим, что зависимость среднего значения какой- либо величины (например, R) от некоторой другой величины (t) называется регрессией y=u(х). Уравнение y=u(х), в котором х играет роль "независимой" переменной называется уравнением регрессии, а соответствующий график- линией регрессии величины у по х. Если регрессия у по х линейная, то можно записать, что

,

где m_y m_x- математическое ожидание х и у, _x² _y²- дисперсии х и у, r- коэффициент корреляции между х и у. Существенно, что для нормального совместного распределения обе линии регрессии y=u(х) и х=v(у) являются прямыми. Понятие коэффициента корреляции r раскрывается в следующей работе.

Приложение 1

ПРОГРАММА ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ

ЛИНЕЙНОЙ РЕГРЕССИИ

REM ************ f(x)=kx+b ********************

CLS

INPUT "введите количество n : ", n

DIM x(n): DIM y(n)

REM ********* заполнение массивов *************

FOR i = 1 TO n

PRINT "x ("; i; ") ="; : INPUT "", x(i)

PRINT "y ("; i; ") ="; : INPUT "", y(i)

NEXT i

REM *******************************************

REM********************************************

FOR i = 1 TO n

L = L - x(i) * y(i): REM L=S(-yx)

M = M + x(i) * x(i): REM M=S(x¤)

NN = NN + x(i): REM NN=S(x)

R = R + y(i): REM R=S(y)

NEXT i

REM *******************************************

REM********************************************

k = (L * n + R * NN) / (NN ^ 2 - M * n)

b = (R - k * NN) / n

PRINT "Имеем зависимость вида: y = k * x + b, где"

PRINT "k = "; k

PRINT "b = "; b