Тема 8. Задачі дробово-лінійного програмування. Основні методи їх розв’язування та аналізу Економічна і математична постановка задачі дробово–лінійного програмування

Розв’язуючи економічні задачі, часто як критерії оптимальнос­ті беруть рівень рентабельності, продуктивність праці тощо. Ці показники математично виражаються дробово-лінійними функціями. Загальну економіко-математичну модель у цьому разі записують так (розглянемо задачу визначення оптимальних обсягів виробництва продукції): позначимо через прибуток від реалізації одиниці -го виду продукції, тоді загальний прибуток можна виразити формулою: ; якщо — витрати на виробницт­во одиниці -го виду продукції, то — загальні витрати на виробництво. У разі максимізації рівня рентабельності вироб­ництва цільова функція має вигляд:

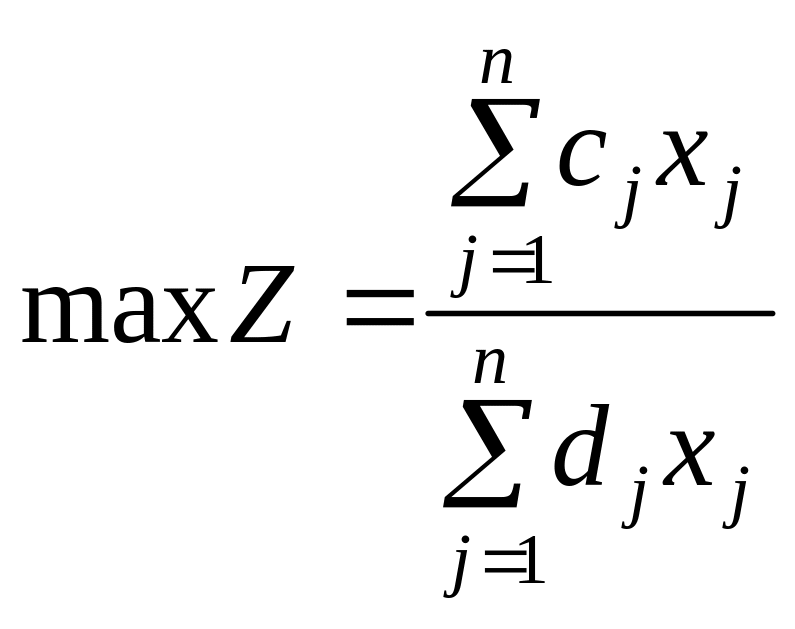(1)

за умов виконання обмежень щодо використання ресурсів:

; (2)

. (3)

Передбачається, що знаменник цільової функції в області допустимих розв’язків системи обмежень не дорівнює нулю.

Очевидно, що задача (1)—(3) відрізняється від звичайної задачі лінійного програмування лише цільовою функцією, що дає змогу застосовувати для її розв’язування за певного модифікування вже відомі методи розв’язання задач лінійного програмування.

Розв’язування дробово-лінійної задачі зведенням до задачі лінійного програмування

Нехай потрібно розв’язати задачу (1)—(3).

Позначимо

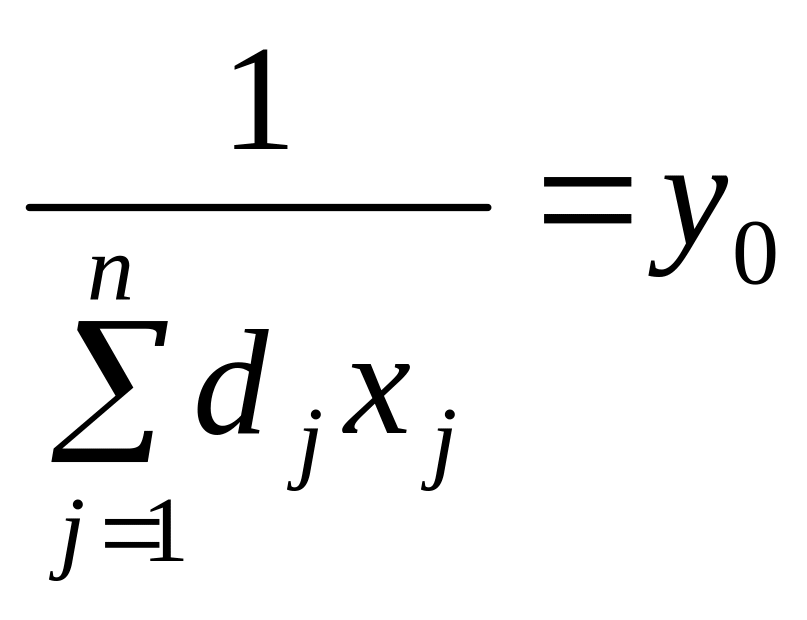
і введемо заміну змінних . Тоді цільова функція (1) матиме вигляд:

.

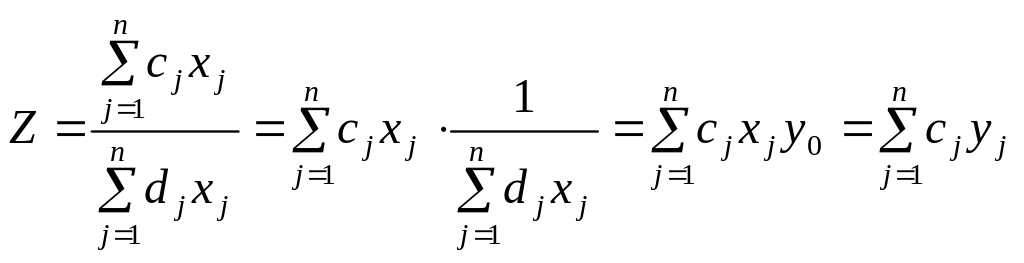Отримали цільову функцію, що виражена лінійною залежністю.

Оскільки , то звідси маємо: . Підставимо виражені через нові змінні значення в систему обмежень (2):

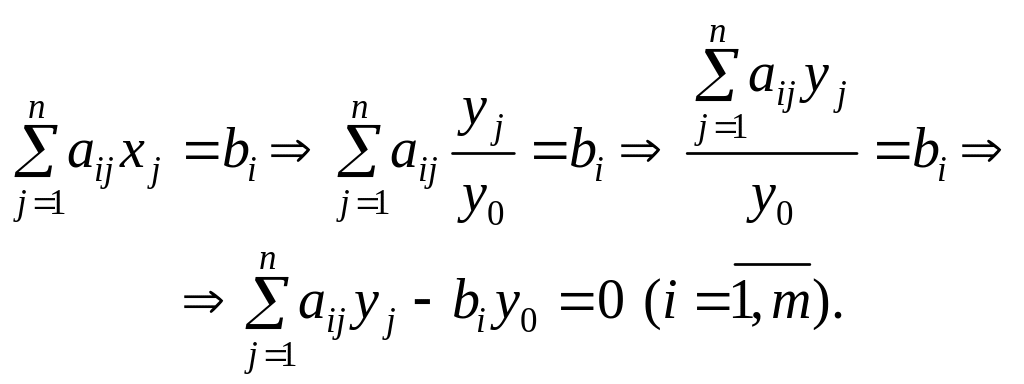
Крім того, з початкової умови

.

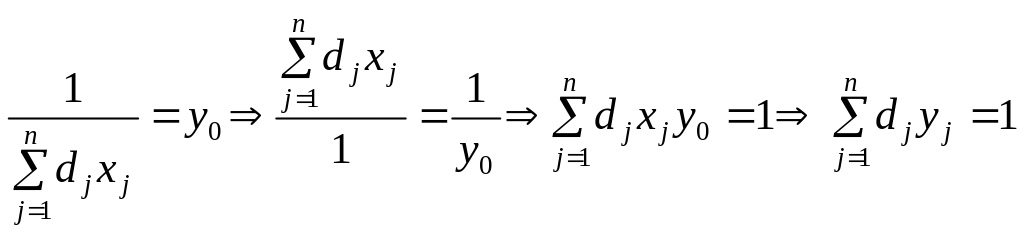Умова (3) стосовно невід’ємності змінних набуває виг­ляду:

.

Виконані перетворення приводять до такої моделі задачі:

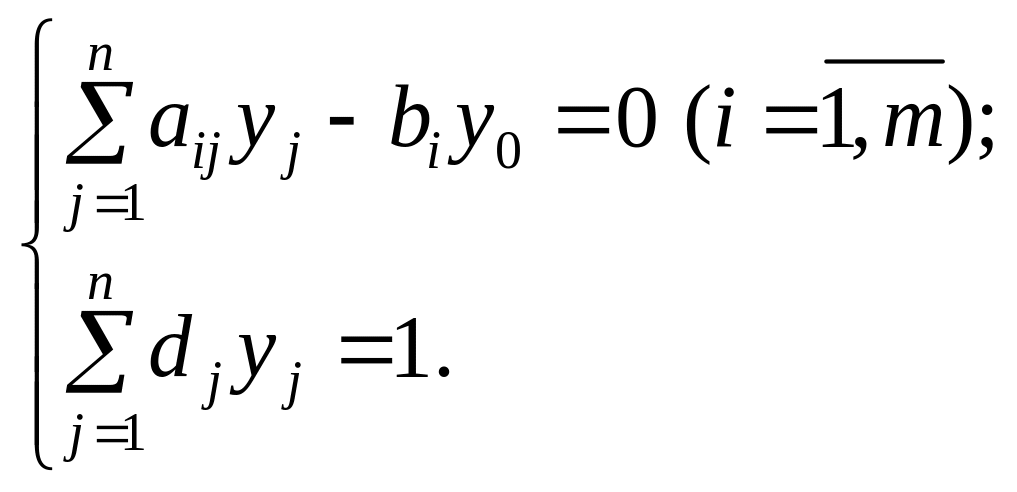
Отримали звичайну задачу лінійного програмування, яку мож­на розв’язувати симплексним методом.

Допустимо, що оптимальний розв’язок останньої задачі існує і позначається:

.

Оптимальні значення початкової задачі (1)—(3) визначають за формулою: .

Тема 9. Економічна постановка і математична модель задачі нелінійного програмування

Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на припущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Якщо такі зв’язки насправді є нелінійними, то більш адекватні математичні моделі доцільно формулювати в термінах нелінійного програмування.

Нехай для деякої виробничої системи необхідно визначити план випуску продукції, за умови найкращого способу використання ресурсів системи. Відомі загальні запаси кожного ресурсу, нормативи витрат кожного ресурсу на одиницю продукції та ціна реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різноманітними, наприклад максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та ціни одиниці продукції.

Однак, загально відомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту кінцевої продукції визначається перш за все її ціною, отже в якості цільової функції доцільно розглядати максимізацію не всієї виготовленої, а лише реалізованої продукції. Тоді необхідно визначити також і оптимальне значення ціни одиниці продукції при якій обсяг збуту буде максимальним, для цього її потрібно ввести в задачу як невідому величину, при цьому обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція міститиме добуток двох невідомих величин (оптимальна ціна одиниці продукції та оптимальна кількість відповідного виду продукції) отже є нелінійною. Таким чином маємо задачу нелінійного програмування.

І нарешті будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. В якості величини ризику розповсюджене використання такої величини як дисперсія, тому врахування обмеженості ризику вимагає введення нелінійної функції в систему обмежень, а мінімізація ризику певного процесу досягається за рахунок дослідження математичної моделі з нелінійною цільовою функцією.

Загальна задача математичного програмування формулюється наступним чином:

Знайти такі значення змінних x_j , щоб цільова функція набувала екстремального (максимального чи мінімального значення):

за умов

( )

Якщо всі функції та ( ) є лінійними, то приходимо до задачі лінійного програмування, інакше (хоча б одна з функцій не є лінійною) маємо задачу нелінійного програмування.

Для розробки методів розв’язування окремих типів задач нелінійного програмування важливе значення має поняття сідлової точки, а також визначення необхідних і достатніх умов існування сідлових точок функції Лагранжа в (n+m)-вимірному просторі змінних при довільних умовах, які можуть накладатися на їх знаки.

Розглянемо нелінійну здачу:

Причому на компоненти векторів накладено обмеження по знаку. Позначимо множину точок, що задовольняють такі обмеження .

Функція Лагранжа для цієї задачі має вигляд:

=

Точка називається сідловою точкою функції Лагранжа, якщо для всіх виконується співвідношення

Для диференційованих функцій та знайдемо необхідні умови існування сідлової точки.

Сідлова точка функції виду за означенням задовольняє умову:

маємо необхідні умови сідлової точки:

Сукупність співвідношень становить необхідні умови, які повинна задовольняти сідлова точка функції Лагранжа для точок, що належать множині . При цьому повинна мати частинні похідні по всіх компонентах векторів .