
- •Тема 3. Геометрична інтерпретація задачі лінійного програмування
- •Тема 4. Симплексний метод розв’язування задач лінійного програмування
- •Тема 5: Теорія двоїстості та двоїсті оцінки у лінійному програмуванні
- •Тема 6. Транспортна задача
- •Початковий опорний план
- •Метод північно-західного кута
- •Метод найменшої вартості
- •Метод потенціалів
- •Тема 7.Економічна постановка і математична модель цілочислової задачі лінійного програмування
- •Тема 8. Задачі дробово-лінійного програмування. Основні методи їх розв’язування та аналізу Економічна і математична постановка задачі дробово–лінійного програмування
- •Тема 9. Економічна постановка і математична модель задачі нелінійного програмування
- •Тема 10. Динамічне програмування
- •Тема 11. Теорія ігор
- •Нехай маємо скінченну матричну гру з платіжною матрицею
- •Тема 12. Кількісне оцінювання та управління ступенем ризику
Тема №1. Концептуальні аспекти математичного моделювання економіки
Розв’язування економічної задачі складається з побудови економіко-математичної моделі, підготовки інформації, отримання оптимального плану, економічного аналізу отриманих результатів і визначення можливостей їх практичного застосування.
Математична модель економічного об’єкту (системи) – це його спрощений образ поданий у вигляді сукупності математичних співвідношень (рівнянь, нерівностей, логічних співвідношень, графіків тощо).
Етапи економіко-математичного моделювання
Проаналізуємо послідовність і зміст етапів одного циклу економіко-математичного моделювання.
1. Постановка економічної проблеми та її якісний аналіз. Головне тут — чітко сформулювати сутність проблеми, мети дослідження, припущення, які приймаються, і ті питання, на які необхідно одержати відповіді. Цей етап включає виокремлення найважливіших рис і властивостей об'єкта, що моделюється, і абстрагування від другорядних; вивчення структури об'єкта і головних залежностей, що поєднують його елементи; формулювання гіпотез, що пояснюють поведінку і розвиток об'єкта.
2. Побудова математичних моделей. Це — етап формалізації економічної проблеми, вираження її у вигляді конкретних математичних залежностей і відношень (функцій, рівнянь, нерівностей тощо). Спочатку зазвичай визначається основна конструкція (тип) математичної моделі, а потім уточнюються деталі цієї конструкції (конкретний перелік змінних і параметрів, форма зв’язків).
Таким чином, побудова моделі має кілька стадій. Неправильно думати, що чим більше чинників ураховує модель, тим краще вона «працює» і ліпші дає результати. Те саме можна сказати і про такі характеристики складності моделі, як використовувані форми математичних залежностей (лінійні та нелінійні), урахування чинників випадковості й невизначеності тощо. Надмірна складність і деталізація моделі утруднює процес дослідження. Треба не лише враховувати реальні можливості інформаційного і математичного забезпечення, а й порівнювати витрати на моделювання з одержуваним ефектом (зі зростанням складності моделі приріст витрат може перевищити приріст ефекту). Однією з важливих особливостей математичних моделей є потенційна можливість їх використання для вирішення різноманітних проблем, тому, навіть зустрічаючись з новою економічною задачею, не треба намагатися «винаходити» модель; спочатку необхідно спробувати застосувати для розв'язання цієї задачі вже відомі моделі. Зазначимо, що на практиці використовують банк моделей здійснюють адаптацію відомої моделі до задачі.
3. Математичний аналіз моделі. Метою цього етапу є з'ясування загальних властивостей моделі. Тут часто застосовують математичні прийоми дослідження. Найважливіший момент — доведення існування рішень у сформованій моделі (теорема існування). Якщо поталанить довести, що математична задача не має рішення, то необхідність у наступній роботі за первісним варіантом моделі відпадає; слід скоригувати чи постановку економічної задачі, чи модифікувати її математичну формалізацію.
4. Підготовка інформації. Моделювання висуває жорсткі вимоги до системи інформації. У процесі підготовки інформації широко використовуються методи теорії ймовірностей, теоретичної і математичної статистики. У статистичному економіко-математичному моделюванні результуюча інформація, використовувана в одних моделях, є вихідною для функціонування інших моделей.
5. Числові розв'язки. Цей етап включає розробку алгоритмів для числового розв'язування задачі, складання програм на ЕОМ і безпосереднє проведення розрахунків. Труднощі цього етапу зумовлені передусім великою розмірністю економічних задач, необхідністю опрацювання значних масивів інформації. Звичайно розрахунки на підставі використання економіко-математичної моделі мають багатоваріантний характер. Завдяки високій швидкодії сучасних ЕОМ вдається проводити числові «модельні» експерименти, вивчаючи «поведінку» моделі при різних значеннях деяких умов. Дослідження, які проводяться за допомогою числових методів, можуть стати суттєвим доповненням до результатів аналітичного дослідження. Зазначимо, що клас економічних задач, які можна розв'язувати числовими методами, значно ширший, ніж клас задач, доступних аналітичному дослідженню.
6. Аналіз числових результатів та їх використання. На цьому, завершальному, етапі циклу виникає питання про правильність і повноту результатів моделювання, про рівень практичного застосування останніх.
Класифікація задач математичного програмування
В математичному програмуванні виділяють два напрямки – детерміновані задачі і стохастичні. Детерміновані задачі не містять випадкових змінних і параметрів. Вся початкова інформація повністю визначена. В стохастичних задачах використовується початкова інформація, яка містить елементи невизначеності, або деякі параметри набувають значень відповідно до визначених функцій розподілу. Якщо у відповідних економічних процесах випадкові явища не відіграють істотної ролі, то задачу можна розв’язувати як детерміновану. Кожен з названих напрямків включає класи задач математичного програмування, які в свою чергу діляться на інші класи.
Як детерміновані так і стохастичні задачі можуть бути статичними (однокрокові) або динамічними (багатокрокові). Оскільки економічні процеси розвиваються в часі, відповідні економіко-математичні моделі мають відбивати динаміку. Поняття динамічності пов’язане зі змінами об’єкту (системи, процесу) у часі.
Далі задачі математичного програмування поділяють на дискретні і неперервні. Дискретними називають задачі, в яких одна, кілька або всі змінні набувають лише дискретних значень. Серед них окремий клас становлять задачі, в яких одна або кілька змінних набувають цілочислових значень вони мають назву задач цілочислового програмування. Якщо всі змінні можуть набувати будь-якого значення в деяких інтервалах числової осі, то задача є неперервною.
Оскільки в економіко-математичних моделях залежності між показниками описані за допомогою функцій, то відповідно до їх виду всі вище згадані класи задач поділяються на лінійні та нелінійні. Якщо цільова функція та обмеження є лінійними функціями, тобто вони містять змінні xj у першому або нульовому степені. В усіх інших випадках задача буде нелінійною.
Найпростішими з розглянутих класів є статичні, детерміновані, неперервні лінійні задачі. Важливою перевагою таких задач є те, що для їх розв’язування розроблено універсальний метод, який називається симплексним методом. Теоретично кожну задачу лінійного програмування можна розв’язати. Для деяких класів лінійних задач, що мають особливу структуру, розробляють спеціальні методи розв’язування, які є ефективнішими. Наприклад, транспортну задачу можна розв’язати симплексним методом, але ефективнішими є спеціальні методи, наприклад метод потенціалів.
Економічні та технологічні процеси, як правило, є нелінійними, стохастичними, розвиваються в умовах невизначеності. Розв’язувати такі задачі набагато складніше, ніж лінійні, оскільки немає універсального методу розв’язування. Для окремих типів нелінійних задач розроблено численні спеціальні ефективні методи розв’язування. Проте слід зазначити, що на практиці застосовують, здебільшого, лінійні економіко-математичні моделі. Часто нелінійні залежності апроксимують (наближають) лінійними. Такий підхід на практиці є доволі ефективним.
У нелінійному програмуванні (в залежності від функцій, які використовуються в економіко-математичній моделі) виокремлюють такі підкласи: опукле програмування — цільова функція вгнута, якщо вона мінімізується, та опукла, якщо вона максимізується, Квадратичне програмування — цільова функція квадратична, а обмеження лінійні.
Щойно було розглянуто лише найбільші класи задач математичного програмування. Можна також за різними ознаками виокремити й інші підкласи. Це особливо стосується задач лінійного, нелінійного і стохастичного програмування. Наприклад, як окремий клас розглядають дробово-лінійне програмування, коли обмеження є лінійними, а цільова функція — дробово-лінійна. Особливий клас становлять задачі теорії ігор, які широко застосовуються в ринковій економіці. Адже тут діють дві чи більше конфліктні сторони, які мають частково або повністю протилежні цілі. У сукупності задач теорії ігор, у свою чергу, також виокремлюють певні підкласи. Наприклад, ігри двох осіб із нульовою сумою.
Тема №2.Задачі лінійного програмування та методи їх розв’язання
Загальна математична модель лінійного програмування
Загальна лінійна математична модель економічних процесів і явищ — так звана загальна задача лінійного програмування подається у вигляді:
![]() (1)
(1)
за умов
![]() (2)
(2)
![]() (3)
(3)
Отже, потрібно знайти значення змінних x1, x2, …, xn, які задовольняють умови (2) і (3), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
Стандартна(симетрична) форма запису ЗЛП
![]()
![]()
Задачу (1) – (3) легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2) всі bi (i = 1, 2, …, m) невід’ємні, а всі обмеження є рівностями.
![]()
Якщо
якесь bi
від’ємне, то, помноживши i-те обмеження
на (–1), дістанемо у правій частині
відповідної рівності додатне значення.
Коли i-те
обмеження має вигляд нерівності
![]()
![]() ,
то останню завжди можна звести до
рівності, увівши додаткову змінну
xn + 1:
,
то останню завжди можна звести до
рівності, увівши додаткову змінну
xn + 1:
![]() .
.
Аналогічно обмеження
виду
![]() зводимо до рівності, віднімаючи від
лівої частини додаткову змінну хn + 2,
тобто
зводимо до рівності, віднімаючи від
лівої частини додаткову змінну хn + 2,
тобто
![]()
Таким чином, якщо система обмежень задачі містить нерівності, то введенням в кожну нерівність своєї додаткової змінної її можна перетворити на систему рівнянь. При цьому в функціонал задачі кожна додаткова змінна входить з коефіцієнтом рівним нулю.
Домовимося називати вектор Х = (х1, х2, …, хп), координати якого задовольняють системі обмежень (2) і (3) допустимим розв’язком, або допустимим планом задачі. Сукупність допустимих розв’язків (планів) задачі утворює область допустимих розв’язків задачі.
Опорним планом задачі лінійного програмування називається допустимий план, який задовольняє не менш ніж п лінійно незалежних обмежень системи (2) у вигляді строгих рівностей разом з обмеженням (3) щодо знака.
Опорний план називається невиродженим, якщо він містить точно m додатних компонент. У противному разі опорний план є виродженим.
Оптимальним розв’язком (планом) називається той допустимий розв’язок, при якому лінійна функція (1) набуває максимального (мінімального) значення.
Тема 3. Геометрична інтерпретація задачі лінійного програмування
Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.
Розглянемо задачу.
Знайти
![]() (1)
(1)
за умов:
 (2)
(2)
![]() .
(3)
.
(3)
Припустимо, що система (2) за умов (3) сумісна і багатокутник її розв’язків обмежений.
Згідно з геометричною
інтерпретацією задачі лінійного
програмування кожне і-те
обмеження-нерівність у (2) визначає
півплощину з граничною прямою
![]() (і
= 1, 2, …, т).
Системою обмежень (2) графічно можна
зобразити спільну частину, або переріз
усіх зазначених півплощин, тобто множину
точок, координати яких задовольняють
всі обмеження задачі — багатокутник
розв’язків.
(і
= 1, 2, …, т).
Системою обмежень (2) графічно можна
зобразити спільну частину, або переріз
усіх зазначених півплощин, тобто множину
точок, координати яких задовольняють
всі обмеження задачі — багатокутник
розв’язків.
Умова (3) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих с1х1 + с2х2 = const.
Скористаємося для графічного розв’язання задачі лінійного програмування властивостями:
якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків. Якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (1) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:
1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (2) знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
4. Будуємо вектор
![]() ,
що задає напрям зростання значення
цільової функції задачі.
,
що задає напрям зростання значення
цільової функції задачі.
5. Будуємо пряму
с1х1 + с2х2
= const, перпендикулярну до вектора
![]() .
.
6. Рухаючи пряму
с1х1 + с2х2
= const в напрямку вектора
![]() (для
задачі максимізації), знаходимо вершину
багатокутника розв’язків, де цільова
функція набирає екстремального зна-
чення.
(для
задачі максимізації), знаходимо вершину
багатокутника розв’язків, де цільова
функція набирає екстремального зна-
чення.
7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
У разі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:
1. Цільова функція набирає максимального значення в єдиній вершині А багатокутника розв’язків (рис. 2.5).
2. Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 2.6). Тоді задача лінійного програмування має альтернативні оптимальні плани.
3. Задача лінійного програмування не має оптимальних планів: якщо цільова функція необмежена згори (рис. 2.7) або система обмежень задачі несумісна (рис. 2.8).
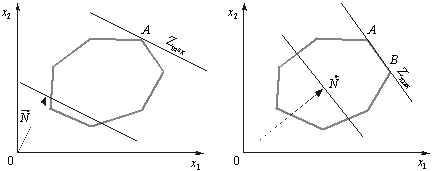
Рис. 2.5 Рис. 2.6
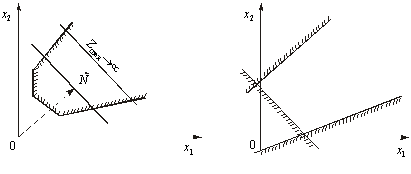
Рис. 2.7 Рис. 2.8
4. Задача лінійного програмування має оптимальний план за необмеженої області допустимих розв’язків (рис. 2.9 і 2.10). На рис. 2.9 у точці В маємо максимум, на рис. 2.10 у точці А — мінімум, на рис. 2.11 зображено, як у разі необмеженої області допустимих планів цільова функція може набирати максимального чи мінімального значення у будь-якій точці променя.
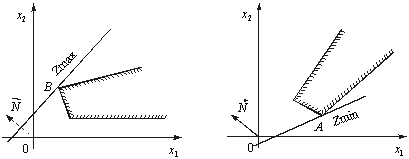
Рис. 2.9 Рис. 2.10

