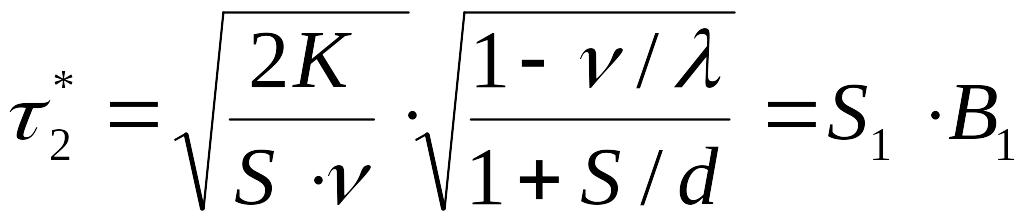- •Система открытого образования
- •Глава I. Основные понятия и методы Экономико-математического моделирования 11
- •Тема 1. Основные понятия и определения 11
- •Тема 2. Основы математического моделирования взаимосвязи экономических переменных 21
- •Тема 3. Оптимизационные методы математики в экономике 34
- •Глава II. Базовый комплекс экономико-математических моделей 52
- •Тема 4.Математические Модели формирования и использования запасов 52
- •Тема 5. Математические модели потребительского поведения и спроса 65
- •Тема 6. Математические модели производственных функций предприятия 101
- •Тема 7. Элементы математических моделей экономического равновесия 143
- •Тема 8. Экономико – математические модели «национальный доход – эффективный спрос». (курсовая работа) 187
- •Тема 9. Экономико – математическое моделирование межотраслеВого равнровесия (курсовая работа) 203
- •Введение
- •Глава I. Основные понятия и методы Экономико-математического моделирования Тема 1. Основные понятия и определения Лекция 1. Основные понятия и определения
- •Понятие и типы моделей. Моделирование
- •З аключение
- •Определение параметров линейного однофакторного уравнения регрессии
- •Параметры линейного однофакторного уравнения регрессии
- •Оценка величины погрешности линейного однофакторного уравнения
- •Некоторые значения t – критерия Стьюдента
- •Проблема автокорреляции остатков. Критерий Дарбина-Уотсона
- •Построение уравнения степенной регрессии
- •Двухфакторные и многофакторные уравнения регрессии
- •З аключение
- •Контрольные вопросы к теме №2
- •Тема 3. Оптимизационные методы математики в экономике Лекция 3. Оптимизационные модели
- •Понятие оптимизационных задач и оптимизационных моделей
- •Оптимизационные задачи с линейной зависимостью между переменными
- •Геометрическая интерпретация оптимизационных задач линейного программирования
- •Симплексный метод решения оптимизационных задач линейного программирования
- •Решение оптимизационной задачи линейного программирования в Excel
- •Двойственная задача линейного програмирования
- •Решение двойственной задачи линейного програмирования
- •Свойства объективно обусловленных оценок и их анализ
- •З аключение
- •Контрольные вопросы к теме №3
- •Построение модели управления запасами в условиях детерминированного спроса Оптимальные партии поставки для однопродуктовых моделей
- •Оптимальные партии поставки для многопродуктовых моделей
- •Определение оптимальных параметров системы управления движением запасов
- •З аключение
- •Контрольные вопросы к теме №4
- •Тема 5. Математические модели потребительского поведения и спроса Лекция 5. Математические модели потребительского поведения и спроса
- •Введение
- •Модели распределения доходов
- •Количественный подход к анализу полезности и спроса
- •Отношение предпочтения и функция полезности
- •Кривые безразличия. Решение задачи об оптимальном выборе потребителя
- •Функции спроса. Коэффициент эластичности
- •Изменение цен и компенсация
- •Заключение
- •Изокванта и ее типы
- •Оптимальная комбинация ресурсов
- •Функции предложения и их свойства
- •Моделирование издержек и прибыли предприятия (фирмы)
- •Данные об объемах выпуска, затратах и прибыли
- •Методы учета научно-технического прогресса
- •Модели фирмы (производителя) (курсовая работа) Издержки предприятия на производство продукции, задача их минимизации
- •Задача минимизации издержек
- •Задача максимизации объема выпуска продукции
- •Заключение
- •Тема 7. Элементы математических моделей экономического равновесия Лекция 7. Основы микроэкономического анализа рынка
- •Рыночное равновесие. Сравнительная статика
- •Моделирование процесса достижения равновесия
- •Моделирование рыночных механизмов в условиях ограниченности ресурсов
- •Модели частного экономического равновесия. Паутинообразная модель рынка (курсовая работа) Паутинообразная модель динамики рыночных цен. Допущения и основные составляющие модели
- •Паутинообразная модель с запаздыванием спроса
- •Паутинообразная модель с запаздыванием предложения
- •Итерационное решение задачи Постановка задачи
- •Дополнительные примеры. Анализ полученных результатов
- •Заключение
- •«Цены предшествующего периода Текущее предложение Текущий спрос и существующие цены Предложение следующего периода и т. Д.»
- •Контрольные вопросы к теме №7
- •Тема 8. Экономико – математические модели «национальный доход – эффективный спрос». (курсовая работа) Лекция 8. Экономико – математические модели «Национальный доход – эффективный спрос»
- •Введение
- •Определение национального дохода
- •Личный доход после вычета налогов
- •Совокупный личный доход
- •Национальный доход (в узком смысле слова)
- •Процесс кругооборота доходов в снс
- •Счета доходов
- •Счет вторичного распределения доходов
- •Сводный счет распределения доходов
- •Счета использования доходов
- •Счет использования валового национального располагаемого дохода
- •Определение национального дохода. Графики
- •Заключение
- •Контрольные вопросы к теме №8
- •Тема 9. Экономико – математическое моделирование межотраслеВого равнровесия (курсовая работа) Лекция 9. Экономико – математическое моделирование межотраслевого равнровесия
- •Введение
- •Определение равновесного выпуска итеративным методом
- •Основные элементы межотраслевых таблиц и межотраслевого анализа
- •Модель расширяющейся экономики Неймана
- •Контрольные вопросы к теме №9
- •Вопросы к экзамену
- •Литература
- •Экономико-математические методы и модели Курс лекций
- •220007, Г. Минск, ул. Московская, 17.
Построение модели управления запасами в условиях детерминированного спроса Оптимальные партии поставки для однопродуктовых моделей
Модель управления запасами в условиях детерминированного спроса – это модель где интенсивность поступления требований предполагается известной и постоянной во времени. Как известно, на практике спрос почти никогда нельзя указать с определенностью; вместо этого его следует описывать в вероятностных терминах.
Детерминированные модели интересны тем, что позволяют познакомиться с методами анализа, используемыми в более сложных системах. Кроме того, результаты, полученные с помощью этих моделей, дают качественно правильные суждения о поведении системы даже при отказе от гипотезы детерминированного спроса.
На рис.4.1. показан самый общий случай образования (ОА), расходования (АК) запаса, затем возможное образование дефицита (КD) и его удовлетворения (DS). В точке S вновь начинается формирование запаса, так что временной отрезок OS представляет собой продолжительность рассмотренного цикла.
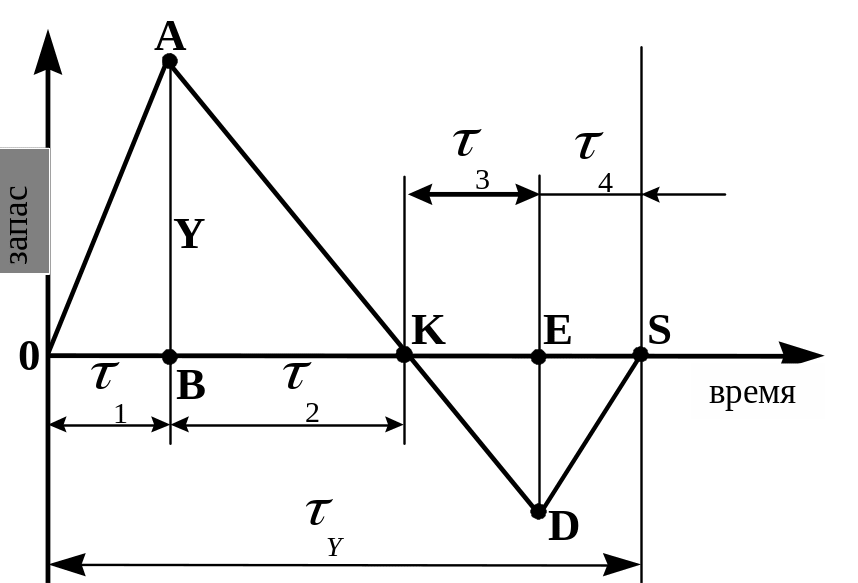
Рис. 4.1. Схема движения запасов для детерминированного спроса.
Таким образом, на рис.4.1. показана схема однопродуктовой модели с учетом неудовлетворенных требований и конечной интенсивностью потребления и расходования запаса, где по оси ординат откладывается величина текущего запаса I, а по оси абсцисс – время t.
Обозначим:
– интенсивность поступления;
– постоянная интенсивность потребления;
1 – продолжительность формирования запаса со скоростью [ед. запаса/ ед. времени];
2 – время расходования запаса со скоростью ;
3 – время образования дефицита со скоростью ;
4 – время погашения дефицита со скоростью .
Тогда (-) – интенсивность (скорость) пополнения запаса.
Максимальный уровень (объем) наличного запаса AB=Y составит:
|
(4-1) |
Максимальный уровень дефицита ED=y составит:
|
(4-2) |
Продолжительность цикла поставки
очередной партии или время возобновления
запаса
![]() :
:
|
(4-3) |
Так как спрос удовлетворяется полностью,
но не всегда своевременно, то величина
партии поставки![]() :
:
|
(4-4) |
Выразив
![]() ,
,
![]() и
и
![]() через
через
![]() и
и
![]() из (4-1) и (4-2) соответственно, получим:
из (4-1) и (4-2) соответственно, получим:
|
(4-5) |
Общие издержки при работе этой системы обеспечения запасами складываются из:
издержек
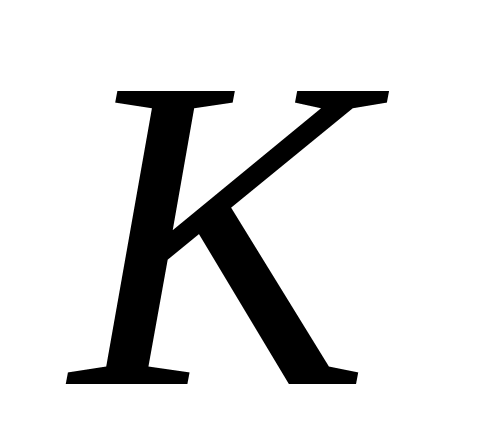 от размещения запасов, которые не
зависят от величины
;
от размещения запасов, которые не
зависят от величины
;издержек от содержания запасов
 ;
;издержек от наличия дефицита
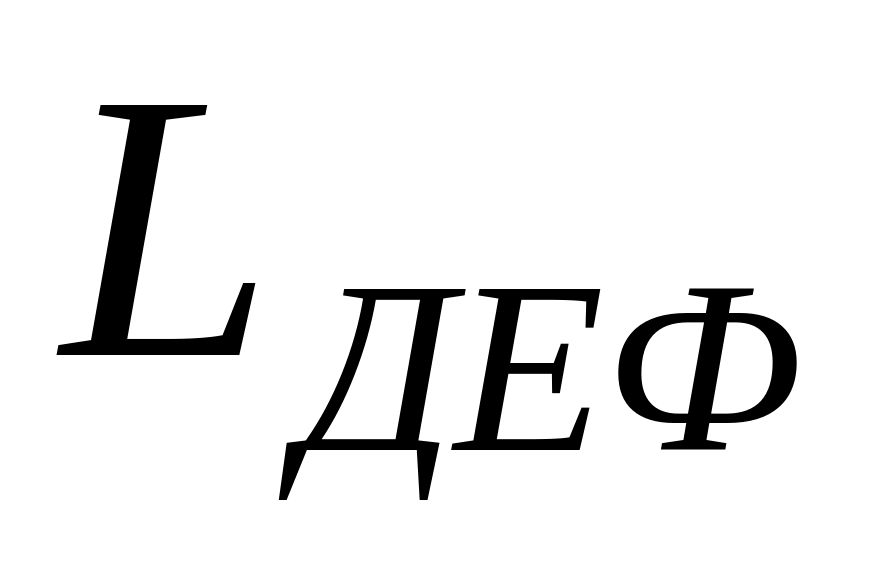 .
.
Величина:
|
(4-6) |
где
![]() – удельные расходы на хранение и
иммобилизацию средств
– удельные расходы на хранение и
иммобилизацию средств
[ руб./ ед. 60 минут].
Потери из-за отсутствия продукции, на которую предъявляются требования, или от дефицита считаем пропорциональными средней величине задолженных требований и времени их осуществления:
|
(4-7) |
где
![]() —
удельные издержки дефицита, т.е. потери,
связанные с нехваткой единицы продукции
в единицу времени.
—
удельные издержки дефицита, т.е. потери,
связанные с нехваткой единицы продукции
в единицу времени.
Учитывая полученные выражения
![]() ,
,
![]() и
,
получим формулу для общих издержек
и
,
получим формулу для общих издержек
![]() в
системе в течении цикла
:
в
системе в течении цикла
:
|
(4-8) |
отсюда удельные издержки за цикл составят:
|
(4-9) |
Найдем оптимальные значения τ2* и τ3* из условия, что:
|
и |
|
(4-10) |
Условия (4-10) позволяют получить систему двух уравнений с двумя неизвестными и :
|
(4-11) |
Обозначим
![]() и разделим первое из уравнений системы
(4-11) на второе, найдем:
и разделим первое из уравнений системы
(4-11) на второе, найдем:
![]() .
.
Откуда
![]() ,
и тогда
,
и тогда
|
(4-12)
|
Подставив (4-12) в любое из уравнений системы (4-11), получим оптимальные значения:
|
(4-13) |
|
(4-14) |
Учитывая (4-13) и (4-14), из (4-5) получим оптимальные значения еще двух составляющих продолжительности цикла возобновления запасов:
|
(4-15)
|
|
(4-16) |
Подставив τ2* и τ2* в формулы (4-5) и (4-4), получим оптимальные значения цикла повторения заказа и партии однопродуктовой поставки:
τц*=√ 2·K/(S·)·√(1+ S / d)/ (1-/)= S1/B1 (4-17)
q* = √ 2·K·/S·√(1+ S / d)/ (1-/)= S2/B1 (4-18)
Аналогично, подставив значения τ2* и τ3* из (4-13) и (4-14) в (4-9), определим оптимальные удельные издержки системы:
Lуд*=√ 2·K··S√ (1-/)/(1+ S / d)= √ 2·K··S· B1 (4-19)
И, наконец, находим оптимальные значения максимального уровня наличного запаса и задолженного спроса:
Y*= √ 2·K·/S·√ (1-/)/(1+ S / d)= √ 2·K·/(S · B1) (4-20)
y*= S / d·√ 2·K·/S·√ (1-/)/(1+ S / d)= S / d·√ 2·K·/(S · B1 ) (4-21)
Общие оптимальные издержки системы за время возобновления запаса составят:
Lобщ *= Lуд* ·τц* (4-22)
Модель с учетом неудовлетворенных требований при конечной интенсивности поступлений можно широко применять при:
управлении поставками материальных ресурсов;
определении оптимальной величины запуска деталей в производство с учетом переналадок на одном и том же технологическом оборудовании.
Во втором случае K – это издержки, связанные с переналадками. Предполагается, что они не зависят от величины выпускаемой партии и порядка запуска деталей в производство, – интенсивность выпуска (производительность), τ1+ τ4 – время, затраченное на производство определенного типа изделий.
Из уравнений (4-13) – (4-22) можно получить ряд других частных моделей:
при большой интенсивности пополнения, когда вся заказанная партия поступает одновременно; это значит, что >> и тогда можно принять /0.
при больших штрафах за допущение дефицита S/d0, т.е. дефицит недопустим (d>>S).
когда пункты а) и b) действуют одновременно. т.е. /0, S/d0, тогда имеем:
q* = √ 2·K·/S
τц*=√ 2·K/(S·)
Lуд*=√ 2·K··S
Последняя модель в отечественной и зарубежной литературе получила название Уилсона.
Применяя формулы (4-17) – (4-19), можно показать, что за счет разумного компромисса между затратами на содержание и потерями от дефицита можно уменьшить общие затраты в единицу времени в √1+S/d раз. При /0 и высоких штрафах за дефицит рассматриваемая модель превращается в модель Уилсона.