2.1.5. Колебания в электрических цепях
Колебания в электрических цепях, содержащих электроемкость С и индуктивность L, описываются теми же дифференциальными уравнениями, что и механические колебания. Рассмотрим следующую задачу.
Задача 3.
Электрическая цепь составлена из катушки индуктивностью L и двух конденсаторов емкостью С1 и С2 (см. рис. 8). Один из конденсаторов подключен к половине катушки. В начальный момент времени ток через катушку отсутствует, напряжение на конденсаторе С1 равно U0. Конденсатор С2 не заряжен. Найти зависимость напряжения на конденсаторе С2 от времени после замыкания ключа К. Принять С1 = С2 = С.
Решение.
Будем считать, что магнитный поток через любой виток ка
Р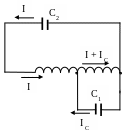
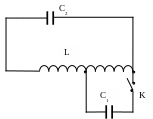ис.
8. Схема соединений до замыкания ключа
и после.
тушки один и тот же (рассеяния магнитного потока нет). По этой причине напряжение U2 на конденсаторе С2 в любой момент времени в два раза больше напряжения U1 на конденсаторе С1: U2 = 2 U1. В начальный момент, сразу после замыкания ключа, заряды на конденсаторах перераспределяются так, чтобы удовлетворить закону сохранения заряда и отмеченному соотношению между напряжениями. Пусть U21 и U11 – новые напряжения на втором и первом конденсаторах соответственно. Тогда
CU0 = CU11+ CU21 = CU11+ 2CU11 = 3CU11
Отсюда
U11
=
U0
, U21
=
U0
.
Поскольку
ток через конденсатор С2
равен Ic2
=
=
,
а ток через конденсатор С1
равен Ic1
=
,
то
Ic2 = I = 2 Ic1 = 2 Ic .
Суммарный магнитный поток Ф через все витки равен сумме потоков Ф1 и Ф2 через витки левой и правой частей катушки соответственно:
Ф
= Ф1
+ Ф2
=
I
+
(I
+ Ic
) =
(2I
+ Ic
) =
LI.
Учитывая, что
-
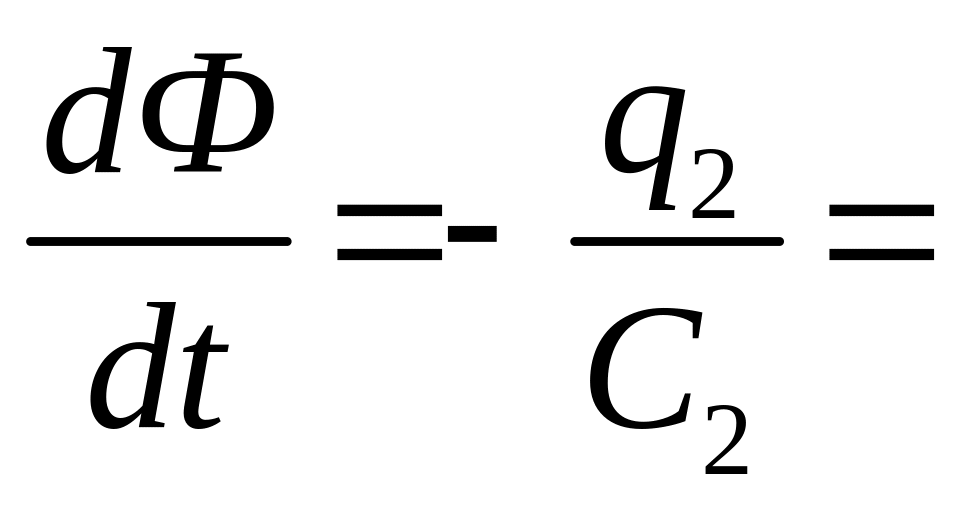U2,
Получаем
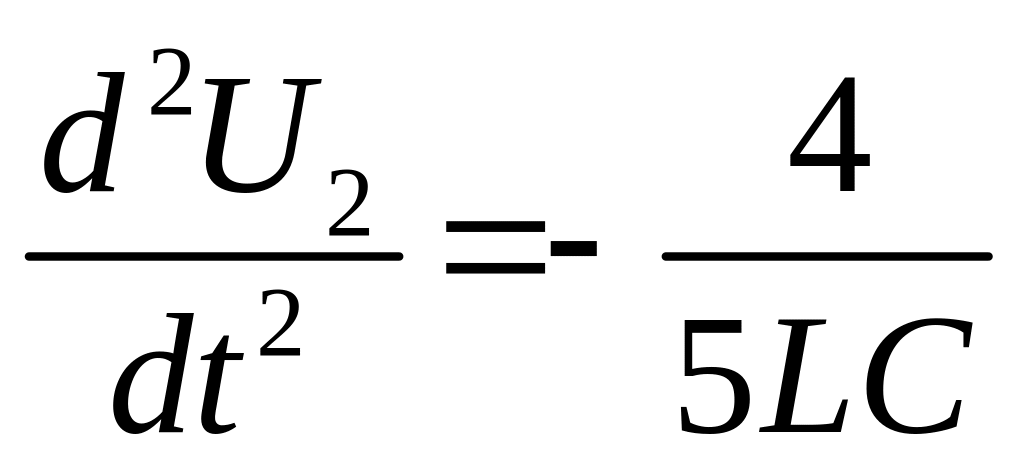U2.
Это
дифференциальное уравнение описывает
гармонические колебания с частотой ω0
=
.
В начальный момент времен t
= 0
U2 = U0. Поэтому окончательно напряжение на конденсаторе С2 изменяется со временем по закону
U2 = U0 cos ω0t.
Таким образом, рассматриваемая система эквивалентна стандартному колебательному контуру с той же индуктивностью L, но с емкостью, равной С. Напряжение на катушке эквивалентного контура в начальный момент равно U0.
2.1.6. Колебания в электростатическом поле
Задача 4. На горизонтально расположенном непроводящем стержне закреплены два маленьких тела, заряженных положительно (заряды нам неизвестны). Еще одно положительно заряженное тело - маленькая бусинка – может двигаться без трения вдоль стержня (рис. 9а). Бусинка совершает малые колебания около положения равновесия. Во сколько раз изменится период таких колебаний, если расстояние между неподвижными зарядами уменьшится вдвое (разумеется, их для этого придется переустановить)?
Решение
Пусть
один из неподвижных зарядов равен Q
и расстояние от него до равновесного
положения бусинки с зарядом q
составляет L.
Тогда для второго заряда, равного nQ,
это расстояние составит L
.
Сместим теперь заряд q
вдоль прямой на очень малое расстояние
х
в сторону заряда nQ.
Тогда сила, действующая на бусинку,
будет равна
.
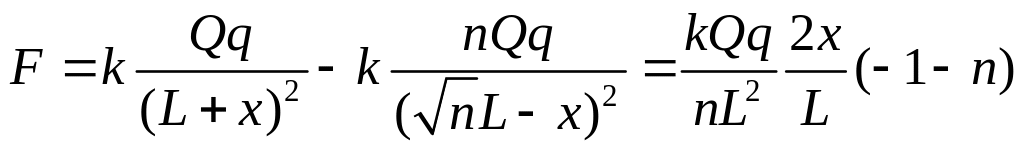Мы пренебрегаем слагаемыми вида (x/L)2 по сравнению с величинами x/L. Видно, что
ω2
.
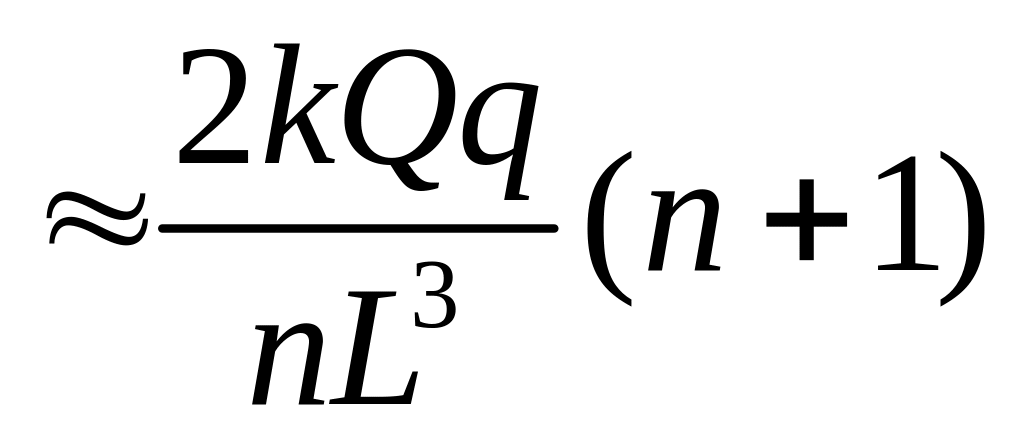Р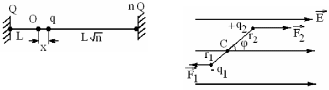
ис.
9. Колебания заряда на стержне (задача
4) и колебания диполя в однородном
электрическом поле (задача 5).
Задача 5. Электрический диполь состоит из двух заряженных тел с отношением заряда к массе η1 = q1/m1 и η2 = q2/m2 соответственно. Расстояние между телами фиксировано и равно L. Диполь помещен в однородное электрическое поле с напряженностью Е (рис. 9б). При каких условиях возможны малые колебания диполя и какова их частота? Силой тяжести пренебречь.
Решение
Колебания
возможны только около положения
устойчивого равновесия, которое
реализуется, если дипольный момент
параллелен вектору напряженности поля
(
).
Если заряды не равны по величине, то
система, установившись вдоль силовой
линии, будет двигаться по ней с ускорением
и совершать малые (гармонические) колебания около этой силовой линии. Пусть φ – малый угол отклонения оси диполя от положения устойчивого равновесия. Пусть точка С – центр масс системы. Колебания будут совершаться относительно оси перпендикулярной силовым линиям проходящей через С. Уравнение моментов:
Jc φ" = - M; (54)
Jc – момент инерции системы относительно указанной оси, М - момент электростатических сил относительно этой же оси. Т.к. массы сосредоточены на материальных точках, то
Jc = m1r12+ m2r22,
где r1 и r2 – расстояния от точки С до соответствующих масс.
Суммарный момент сил
M = (q1r1 + q2r2) E sin φ.
С учетом малости угла уравнение колебаний примет вид
Jc φ" = - (q1r1 + q2r2) E φ.
Отсюда для собственной частоты ω0 имеем:
ω02
=
.
Воспользуемся тем, что для центра масс m1r1 = m2r2 и r1 + r2 = L, что позволяет выразить отсюда r1 и r2:
r1
=
,
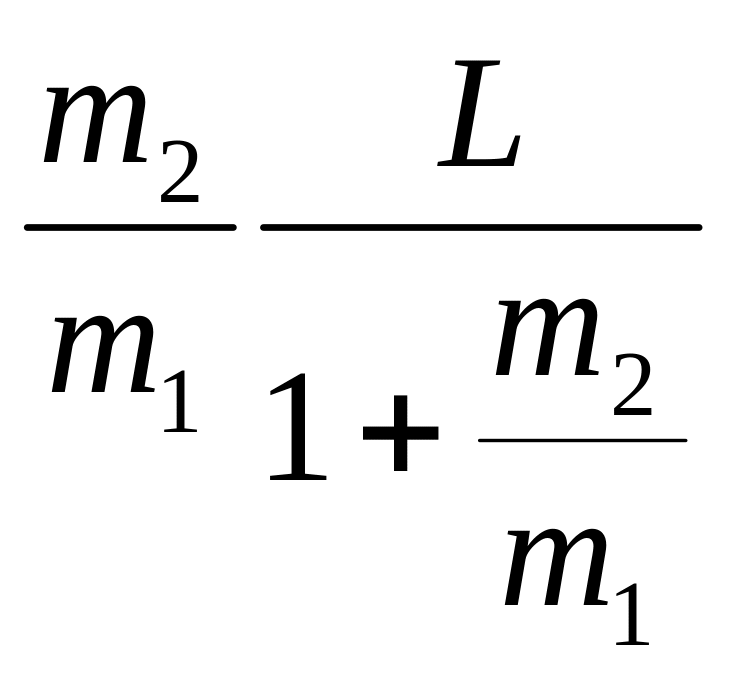r2
=
.
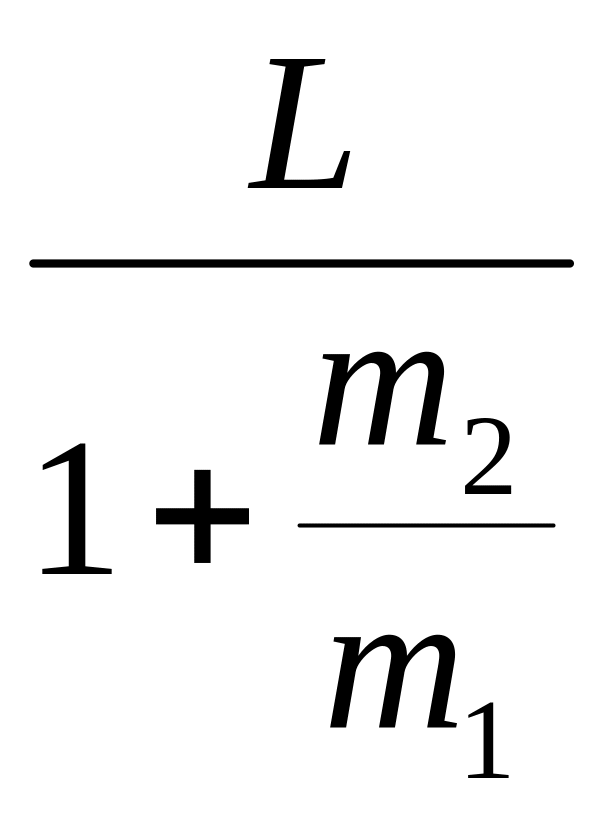Окончательно имеем
ω02
=
=
.