2.1.3. Пружинный маятник

В качестве другого примера гармонического осциллятора рассмотрим пружинный маятник – материальную точку массой m, прикрепленную к одному концу идеальной невесомой пружины жесткостью к, другой конец которой закреплен. Длина пружины в нерастянутом положении равна .

Пусть на материальную точку массой m действует, кроме силы упругости пружины , постоянные силы , , … , не зависящие от удлинения пружины, ни от кинематических характеристик движения материальной точки (например, ее скорости). В положении равновесия

= ,

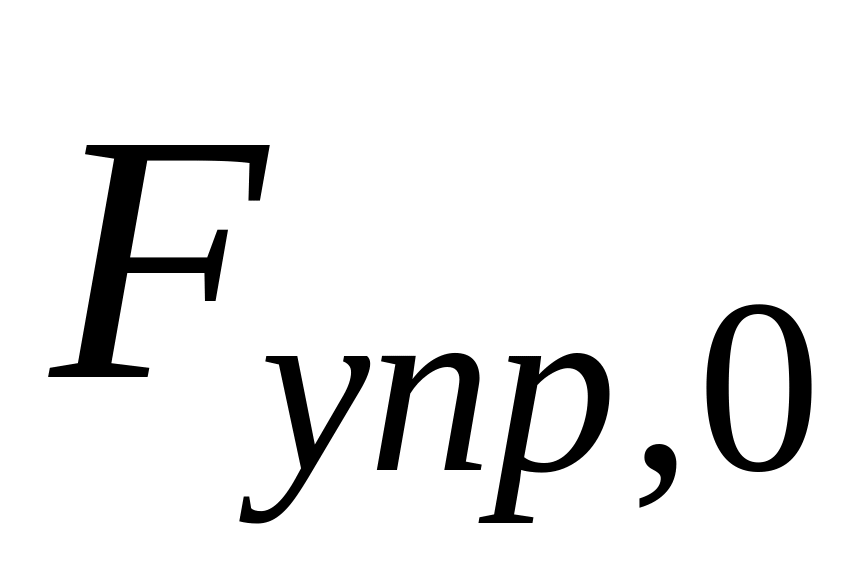т.е. пружина будет расположена вдоль равнодействующей силы и растянута (или сжата) на величину

Δl = 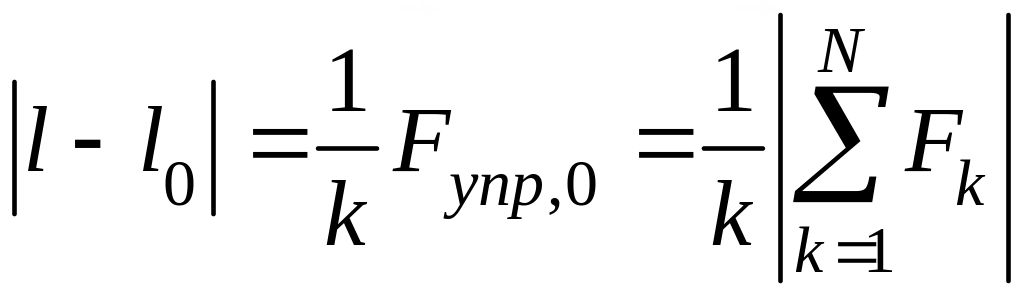. (49)

Если теперь вывести пружину из положения равновесия, растянув или сжав ее на величину x, отсчитываемую от положения равновесия, то равнодействующая сила не изменится, а сила упругости увеличится на величину kx. В результате этого появиться результирующая сила, направленная в сторону положения равновесия (возвращающая сила) и равная

F_x = - kx

Отсюда видно, что возвращающая сила линейно зависит от смещения x, причем коэффициент возвращающей силы равен жесткости пружины

k = к,

а это означает, что пружинный маятник будет совершать гармонические колебания с частотой

ω₀ = (50)

и периодом

T = 2π

около положения равновесия, в котором пружина растянута на величину, определяемую выражением (49).

Обратим внимание, что собственная частота (и период) колебаний пружинного маятника определяется лишь жесткостью пружины и массой маятника и не зависит от внешних сил , , … , действующих на него, от которых зависит лишь растяжение пружины в положении равновесия. Поэтому, где бы ни находился пружинный маятник (в шахте, на вершине горы или на борту спутника) и как бы ни двигалась точка закрепления пружины, его частота и период колебаний будут всегда одними и теми же.

Коэффициент жесткости характеризует пружину в целом и зависит как от свойств материала, из которого она изготовлена, так и от ее геометрических характеристик. Некоторое представление об этих зависимостях можно получить на основании следующей модели. Заменим пружину стержнем длины L и сечения S. Пусть на стержень действует деформирующая (растягивающая или сжимающая) сила F. Она создает в стержне механическое напряжение σ = и удлиняет его на х. Относительное удлинение составляет ε = . Закон Гука представим в виде ε = . Здесь Е – модуль Юнга. Сравнивая с F = kx, получим k = . Жесткость пружины обратно пропорциональна ее длине.

2.1.4. Комбинированные осцилляторы

Комбинированный осциллятор - маятник, находящийся под воздействием нескольких сил различной физической природы, обеспечивающих возвращение отклоненного тела к одному и тому же положению устойчивого равновесия. Будем считать, что осциллятор совершает одномерные движения. Поэтому комбинацию математического маятника и пружинного маятника, показанную на рис. 6, рассматривать не будем, поскольку здесь меняются как угол отклонения, так и длина маятника. Это колебания с двумя степенями свободы.

Задача 2. Положительный заряд q сосредоточен на материальной точке массой m, которая подвешена в вакууме на невесомой нерастяжимой непроводящей нити длины l на высоте h над провод-

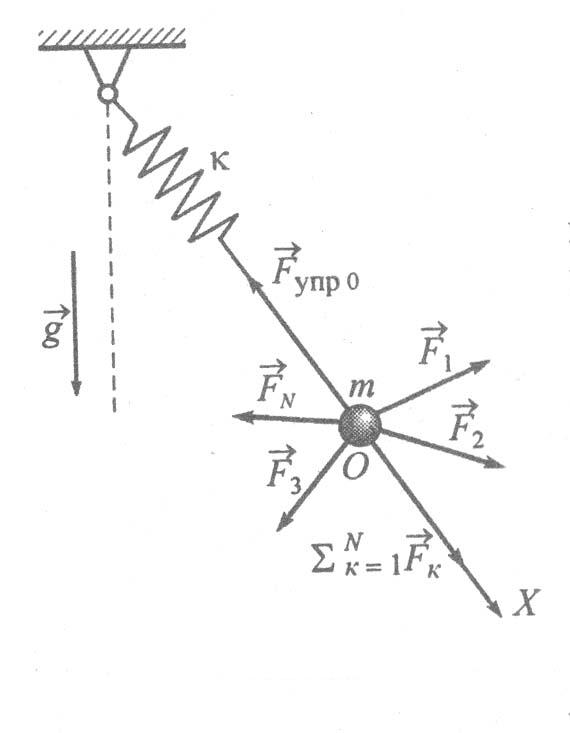
Рис.6. Математический маятник на упругом подвесе

ником (электропроводность которого бесконечна), занимающим нижнее полупространство. Граница раздела вакуума и металла – плоскость. Материальную точку отклоняют на малый угол от положения устойчивого равновесия. Найти собственную частоту колебаний такого комбинированного осциллятора.

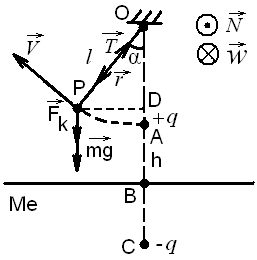
Рис.7. Заряженная материальная точка, колеблющаяся над проводящим полупространством.

AB = BC = h ; AD = Δh ; l =  - длина нити; - радиус-вектор, проведенный из точки О в точку Р.

Решение

На точку действуют сила тяжести, сила натяжения нити и сила электростатического (кулоновского) взаимодействия (рис. 7).

Рассмотрим подробнее силу кулоновского взаимодействия F_k.

Заряд +q перераспределяет свободные электроны проводника. В результате на поверхности раздела появляется отрицательный заряд по величине равный заряду q. Между исходным зарядом и наведенными зарядами возникает электростатическое взаимодействие. При колебаниях поверхностные заряды будут перемещаться, возникнут токи, что приведет к выделению джоулева тепла и магнитному взаимодействию. Однако, в хорошем металлическом проводнике (с бесконечной электропроводностью) при малых скоростях движения зарядов этими явлениями можно пренебречь.

Величину и направление кулоновской силы можно найти из сравнения картины силовых линий электрического диполя и картины силовых линий заряда, подвешенного над идеальным проводником. Силовые линии входят в проводник под прямым углом и их густота тем больше, чем ближе точка на поверхности проводника к точке B, лежащей на оси симметрии картины. Таким образом, картина силовых линий для рассматриваемого случая аналогична картине силовых линий диполя с расстоянием между положительным и отрицательным точечными зарядами равным 2h. Тогда F_k =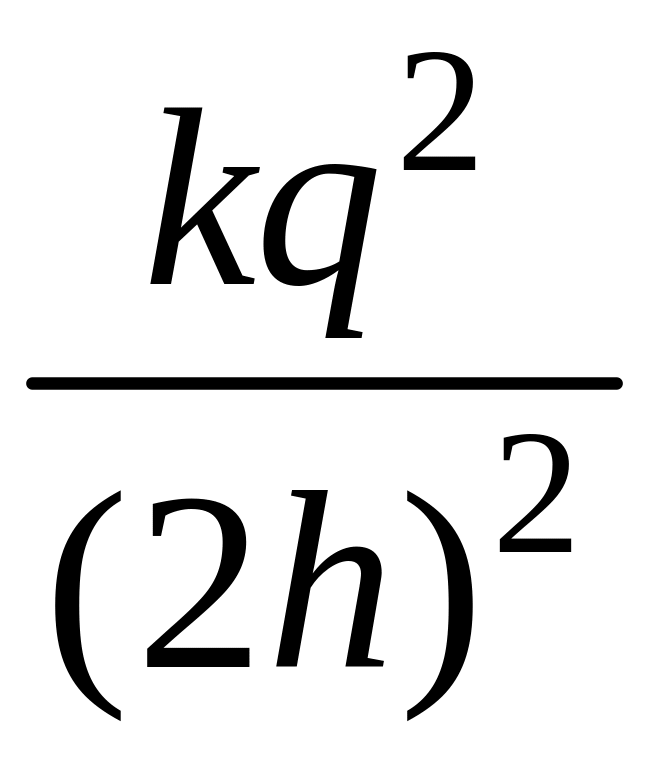 для оси симметрии. Это поле неоднородно, но для малых колебаний момент кулоновской силы, как и момент силы тяжести можно считать пропорциональным углу α.

При отклонении нити на угол α материальная точка поднимается на высоту Δh = l(1 – cos α). Это приводит к изменению величины силы F_k:

F_k = .

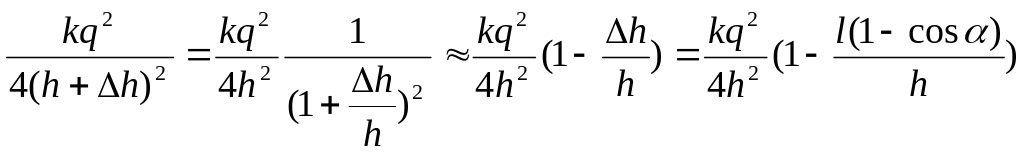Однако, при малых колебаниях, когда

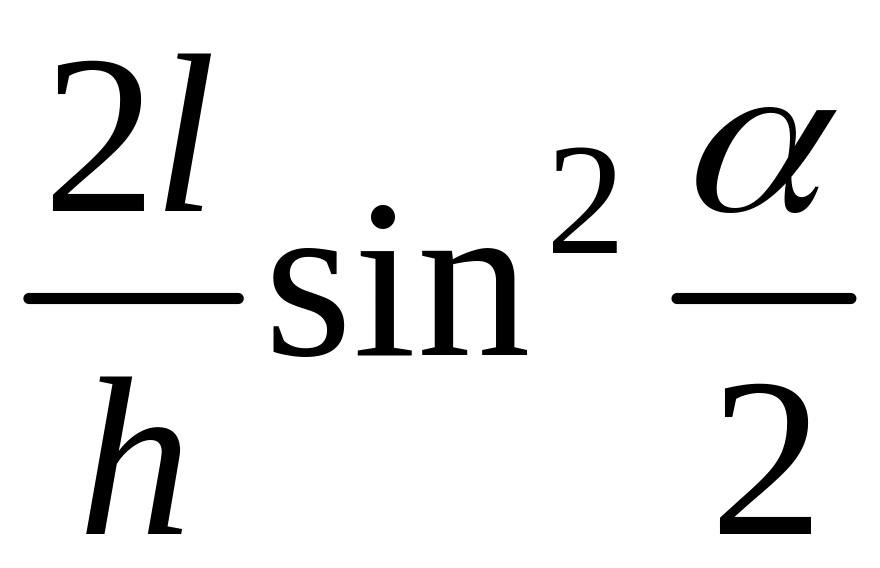<< 1 т.е. << 1

силу кулоновского взаимодействия заданного заряда и наведенных поверхностных зарядов можно считать неизменной.

Момент инерции материальной точки (относительно оси вращения О параллельной поверхности идеального проводника) J₀ = ml², l – длина нити. Момент сил, действующих на материальную точку

N = ( mg + F_k )lsinα . (51)

Здесь PD = l sinα - плечо действующих сил.

Связь между векторами скорости, угловой скорости и вектором направленным от центра вращения по радиусу к материальной точке задается соотношением:

= [ , ]

Если скорость материальной точки направлена влево, то угловая скорость и момент импульса = J₀ направлены против момента сил . Поэтому основное уравнение динамики вращательного движения (уравнение моментов) запишется в виде

J₀α" = - (mg + F_k) lsinα, (52)

где α" = ε = угловое ускорение.

Тогда из (52) для sin α ≈α получаем

α" + lα = 0

В соответствии со стандартными обозначениями ω₀² = , где ω₀ собственная частота. Если бы заряда на материальной точке не было, то ω₀₁² = mg/J₀ . Если бы можно было «отключить» силу тяжести, то ω₀₂² = F_k/J₀ . Поэтому мы можем записать ω₀² = ω₀₁² + ω₀₂² . Если бы возвращающий момент обеспечивали n сил различной физической природы, то

ω₀² = . (53)

Разумеется, это соотношение верно только для малых колебаний.