2.1.17. Добротность

Добротность – очень емкое понятие в теории колебаний. Дело в том, что любая одномерная колебательная система всегда характеризуется двумя основными параметрами: ₀ – собственной частотой и  - коэффициентом затухания. Следует отметить, что понятие коэффициента затухания вводится при условии, что сила трения, действующая на осциллятор, пропорционально скорости F_сопр ~ rV . Если закон сопротивления другой, как, например, при колебаниях с сухим трением, то введение  затруднительно. Пусть указанные два параметра ввести можно; тогда можно ввести и их отношения ₀/₀ - мы получим безразмерный параметр, который и называется добротностью. Иногда в частных исследованиях вводят величины, отличающиеся от ₀/ на некоторый постоянный множитель. Но это ничего не меняет.

При указанных условиях уравнение колебаний имеет вид

х^ + 2 х^ + ₀² х = 0.

Здесь на осциллятор действует только собственная возвращающая сила F_в= -₀²x и сила трения F_т = -2x’, х(t) – любая колеблющаяся физическая величина: смещение частицы от положения устойчивого равновесия, сила тока в колебательном контуре, смещение столбика газа в акустическом резонаторе и т.д.

Решением уравнения (110) при условии ₀ >  является затухающая гармоника (рис. 26)

х(t) = Ае ^-t cos (t + ),

где ² = ₀² - ², а величина а = Ае ^-t может рассматриваться как переменная во времени амплитуда. Пусть  - время, за которое амплитуда уменьшается в е раз, т.е.

А/а = е = е^-

за это время осциллятор успевает совершить N_e колебаний

N_e = /Т = 1/(Т); Т = 2/.

Введем параметр

,

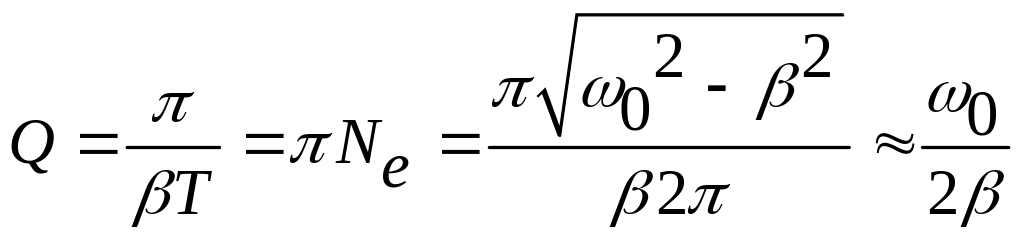называемый добротностью. Из (104) следует, что добротность в  раз больше числа колебаний, совершаемых за такое время, что амплитуда колебаний уменьшается в е раз.

1. Рассмотрим убыль энергии осциллятора при затухающих колебаниях. Запас механической энергии

E = ( к – жесткость пружины)

Отсюда

E = 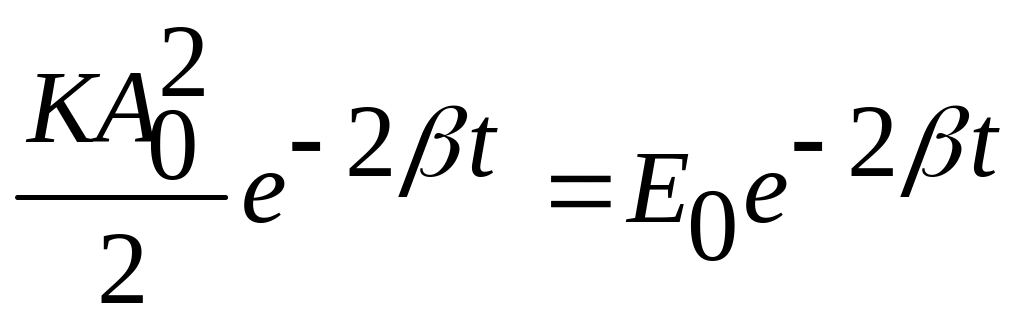(101)

(рис. 24).

здесь Е₀ – начальный запас энергии в системе. Продифференцируем (101) по времени и определим скорость убыли энергии осциллятора:

.

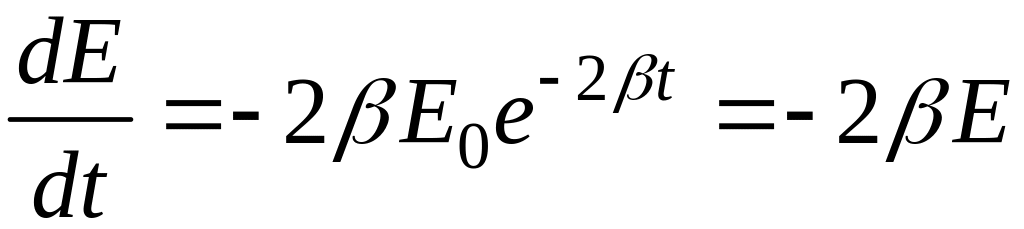Будем считать период колебаний Т достаточно малым, таким, что Т ~ dt, что оправдано для высокодобротных колебаний, тогда изменение энергии за период Е из (101):

.

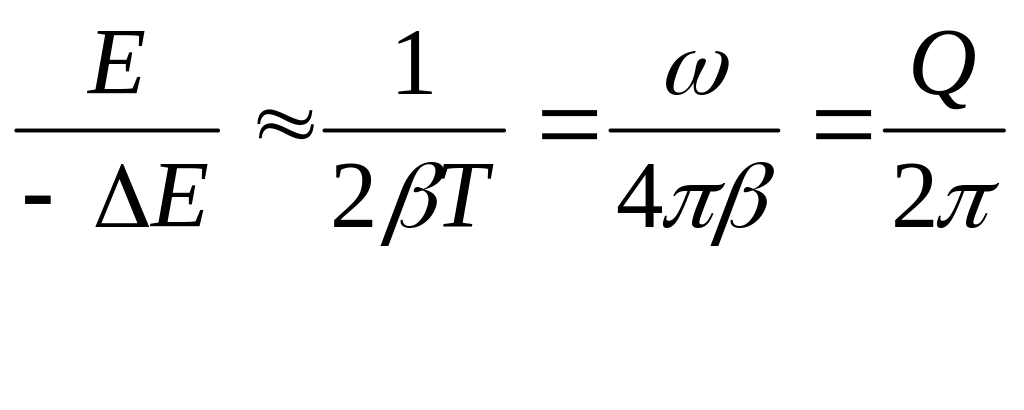Таким образом, добротность осциллятора в 2 раз больше убыли его энергии за период (рис. 24).

2. Рассмотрим вынужденные колебания осциллятора и пусть

внешняя вынуждающая сила F = F₀ cos t будет гармонической. Уравнение вынужденных колебаний возьмем в виде

,

где f = - амплитуда (приведенная) внешней (вынуждающей) силы,  - ее частота.

Решение этого уравнения в виде установившихся колебаний (без учета переходного процесса) имеет вид (86 - 87):

х(t)=Аcos(t+), A() =

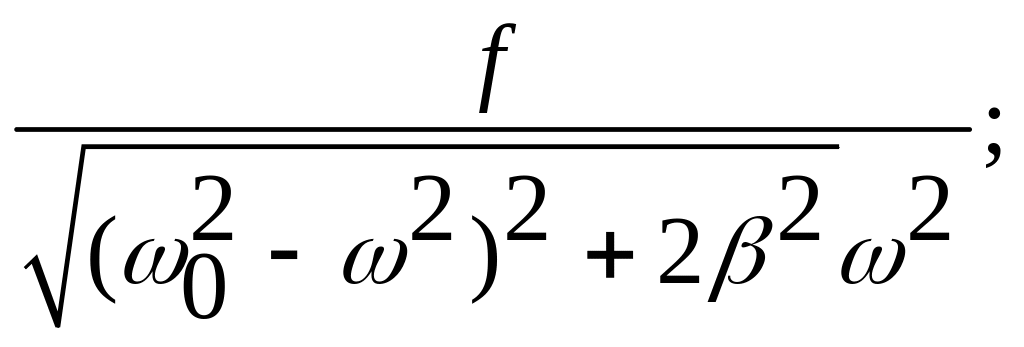
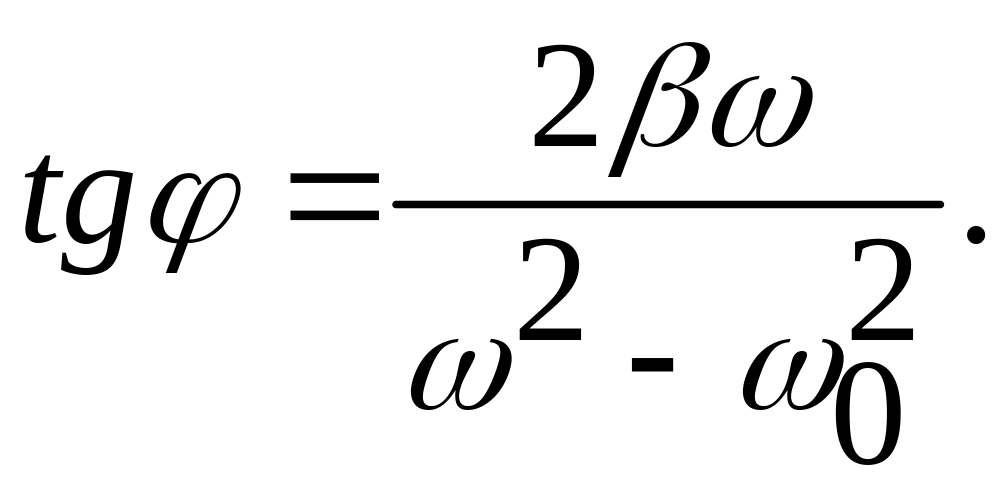
Функция А() – амплитуда установившихся колебаний, она имеет максимум на резонансной частоте

.

На этой частоте амплитуда колебаний (резонансная) имеет значение

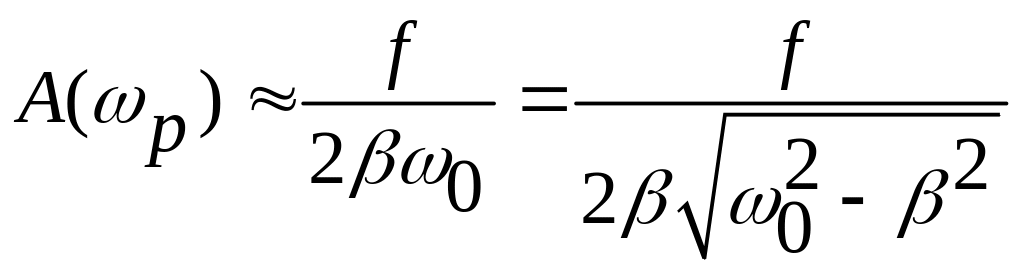. (102)

Эти соотношения уточняют приведенные ранее.

Из (102) находим, что на частоте близкой к нулю

A(0) =

(рис. 27)

Таким образом, слабая внешняя сила, действующая на осциллятор с частотой _р способна раскачать его до амплитуд тем больших, чем меньше . Можно утверждать, что слабый сигнал, поступивший в колебательную систему, усиливается, причем коэффициент усиления, понимаемый как отношение амплитуды на резонансной частоте и на низких частотах, равен

K = 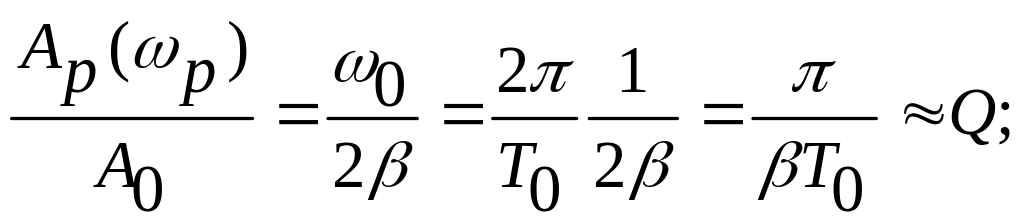(103)

Таким образом, добротность указывает, во сколько раз резонансная амплитуда больше амплитуды установившихся колебаний на низких частотах (рис. 24).

3. Рассмотрим сдвиг фаз между вынуждающей силой и установившимися колебаниями, задаваемый формулой (87). Преобразуем ее к виду

Отсюда при

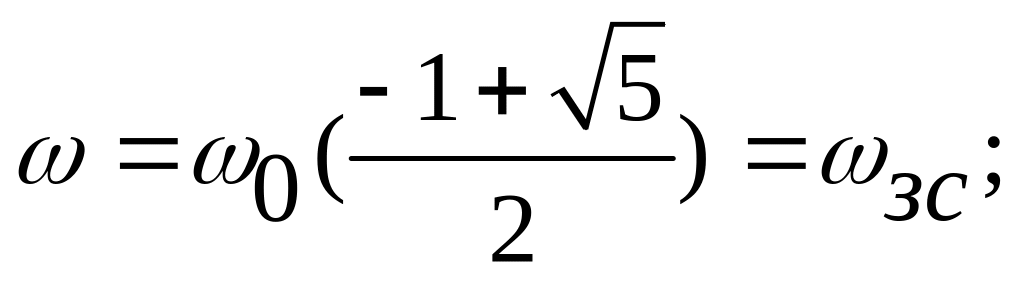
имеет место

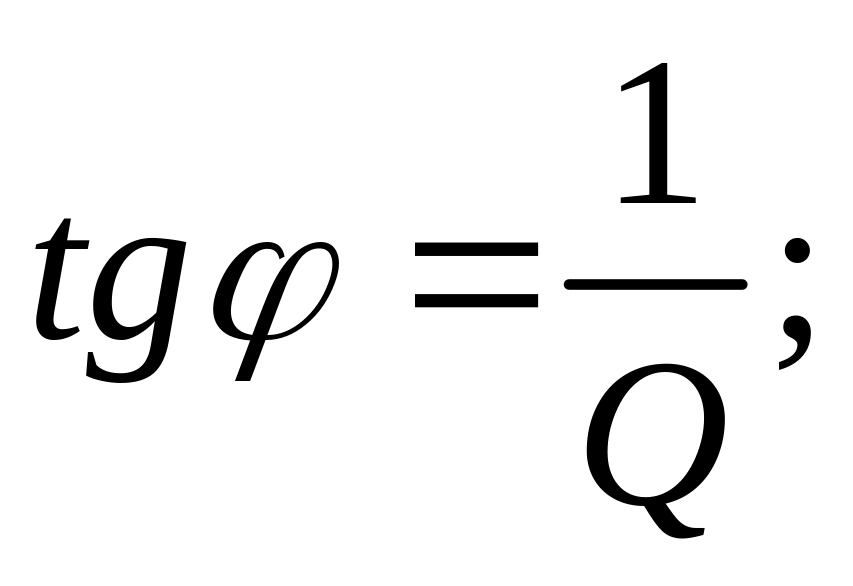
Таким образом, добротность равна котангенсу сдвига фаз на некоторой частоте _3С = 0, 618033988₀ (между вынуждающей силой и установившимися колебаниями)

Установим связь добротности с шириной частотной полосы резонансного контура. Представим схематично этот вывод. Итак, определим частотный диапазон на резонансной кривой, для которого амплитуда вынужденных колебаний в k раз меньше амплитуды в резонансе. Рассмотрим резонанс смещений. Этот диапазон и есть ширина частотной полосы по уровню 1/ k . Имеем

A= f₀/( )= (1/ k)А_рез =(1/ k)f₀/2β (104)

Отсюда

(ω²₀ – ω²)² + 4β² ω² = 4 β²k² (ω²₀ - β²).

Возведем это выражение в квадрат и получим биквадратное уравнение относительно ω :

ω⁴ + ω² (4 β² - 2 ω²₀ ) + ω⁴₀ - 4 β²k² ω²₀ +4 β⁴k² = 0.

Пусть корни этого уравнения ω₁² и ω₂² . Для дальнейшего анализа применим теорему Виетта. Имеем

ω₁² + ω₂² = - (4 β² - 2 ω²₀ )

ω₁² * ω₂² = ω⁴ ₀ - 4 β²k² ω²₀

Членом, содержащим β⁴, мы пренебрегли ввиду его малости.

Составим выражение, содержащее разность частот ω₁ и ω₂ :

(ω₁ + ω₂ )² = ω₁² + ω₂² – 2 ω₁* ω₂ =

= - 4 β² + 2 ω²₀ - 2 .

Составим выражение для относительной ширины частотной полосы

Окончательно имеем:

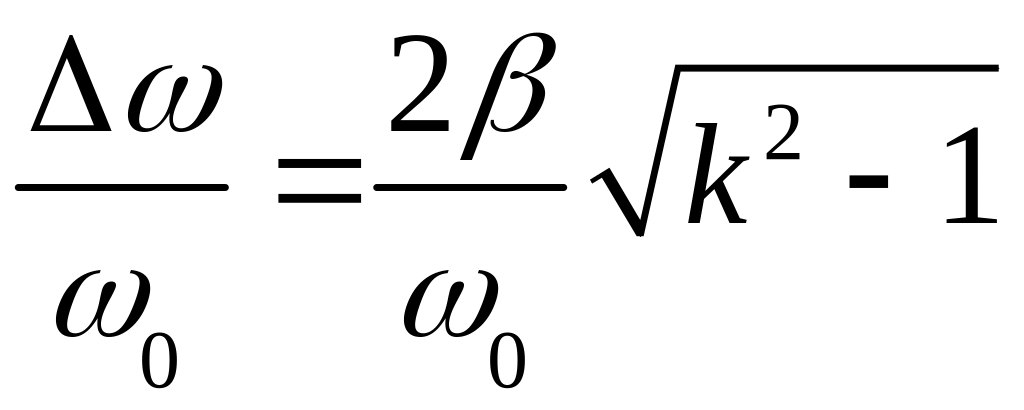. (105)

Таким образом, относительная ширина частотной полости (по уровню 1/k) /₀ обратно пропорциональна добротности осциллятора. Чем выше добротность, тем острее резонансная кривая (рис. 24).

Рассмотрим процесс установления колебаний на частоте близкой к ₀ в осцилляторе, не имеющем затухания ( = 0). Свободные колебания такой осциллятор совершает на частоте ₀

а вынужденные - на частоте вынуждающей силы  близкой к ₀

Общее решение уравнения (80), учитывающее переходной процесс установления вынужденных колебаний и вынужденное колебание, имеет вид

(106)

Пусть колебания начинаются из состояния устойчивого равновесия и состояния покоя, но с ускорением, вызванным внешней силой с амплитудой F₀. Таким образом

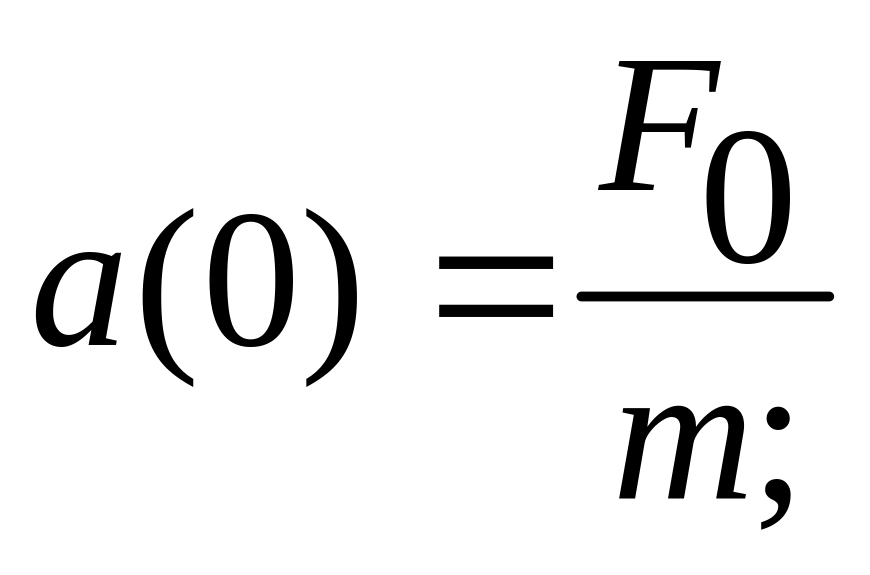(107)

Найдем скорость v (t) и ускорение a(t), продифференцировав (106)

Подставив сюда начальные условия (107), найдем амплитуды A и В (постоянные интегрирования) и получим

B = -A;

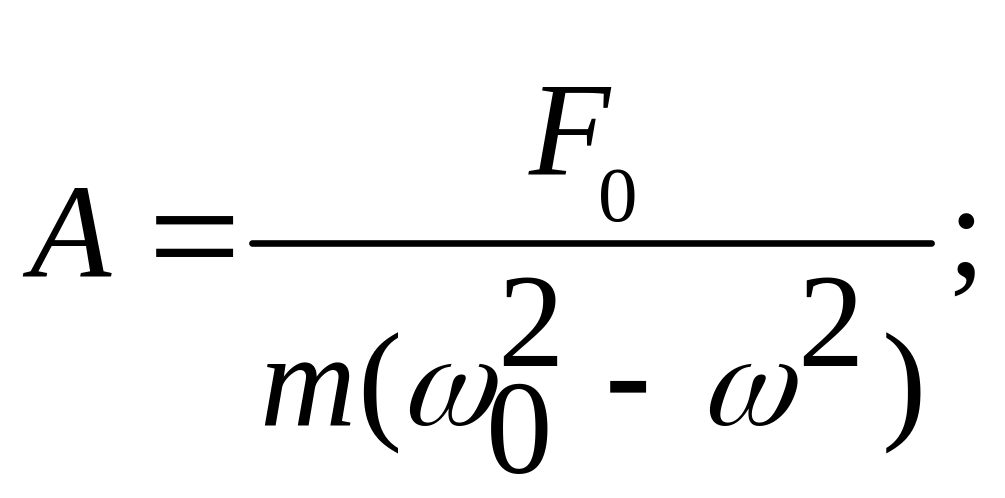
Тогда общее решение (80) примет вид

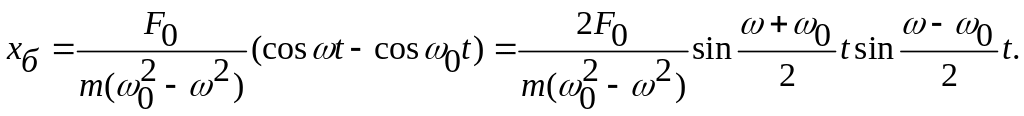
Это выражение представляет собой биения.

Устремим теперь частоту вынуждающей силы  к частоте собственных колебаний осциллятора ₀

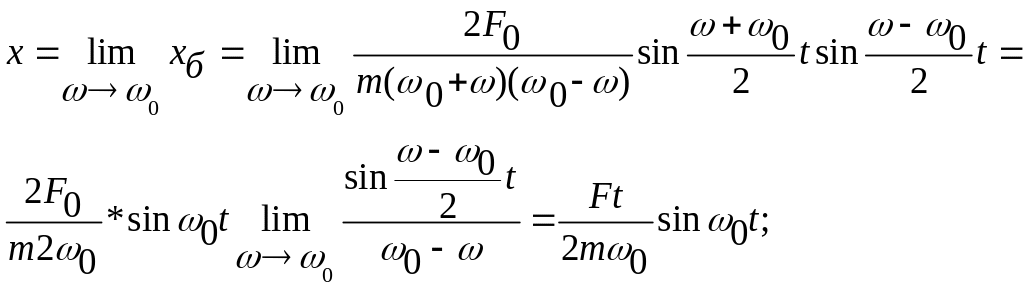
(рис. 24).

Таким образом, амплитуда колебаний при раскачке осциллятора в нашем случае происходит по линейному закону в зависимости от времени. Но раскачка заканчивается, когда амплитуда достигает значения, задаваемого формулой (75). Пусть раскачка продолжается в течение времени , тогда

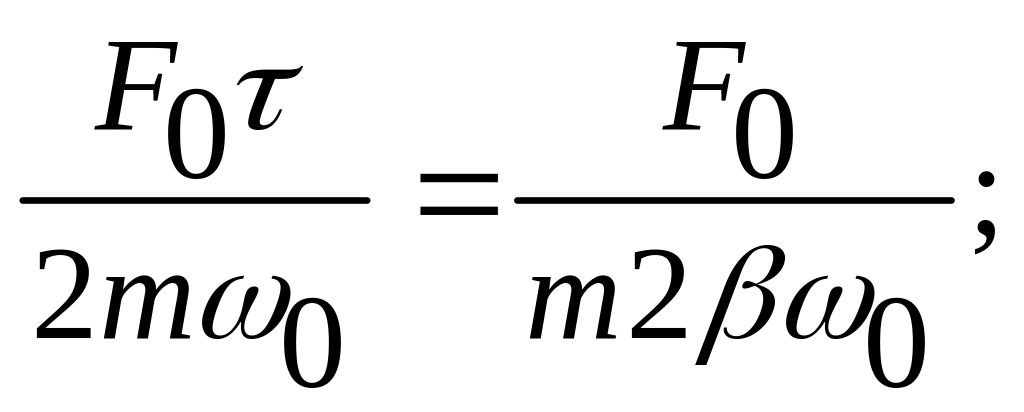
отсюда

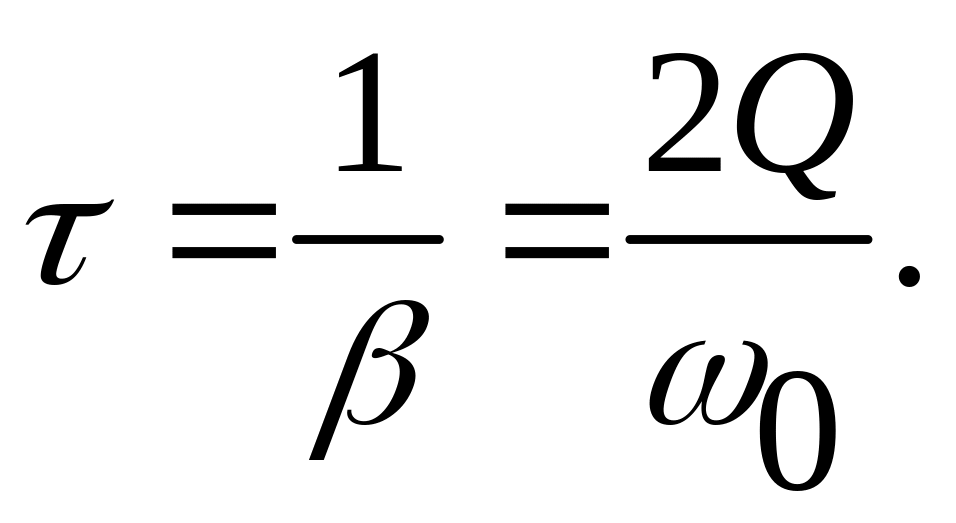(108)

В этом выражении частота ₀ фиксирована. Следовательно, время установления колебаний под действием внешней гармонической силы тем больше, чем выше добротность осциллятора.

Порядки величин добротностей некоторых осцилляторов даны в табл. 3.

Таблица 3

Добротность осцилляторов

Механические (резина) 10 на 100 Гц; 5 на 2*10³ Гц; 3 на 10⁴ Гц;

Акустические резонаторы – 50;

Радиотехнические контуры с частотой ~ 1 МГц – несколько сотен;

Медные резонаторы на СВЧ f >1МГц – 3*10⁴;

Пьезоэлектрические кристаллы (кварц) – 5*10⁵ ;

Колебания ядер атомов в эффекте Мессбауэра – 10¹⁰;

Лазерные колебания (резонатор Фабри-Перо) – 5*10⁶ ;

Пульсары (нейтронные замагниченные звезды) – 7,5*10¹²

(Период 0,033с, замедление вращения и частоты следования импульсов 36,52 нс/сутки = 4,23*10^-13. Период увеличивается в е раз за 2500 лет).

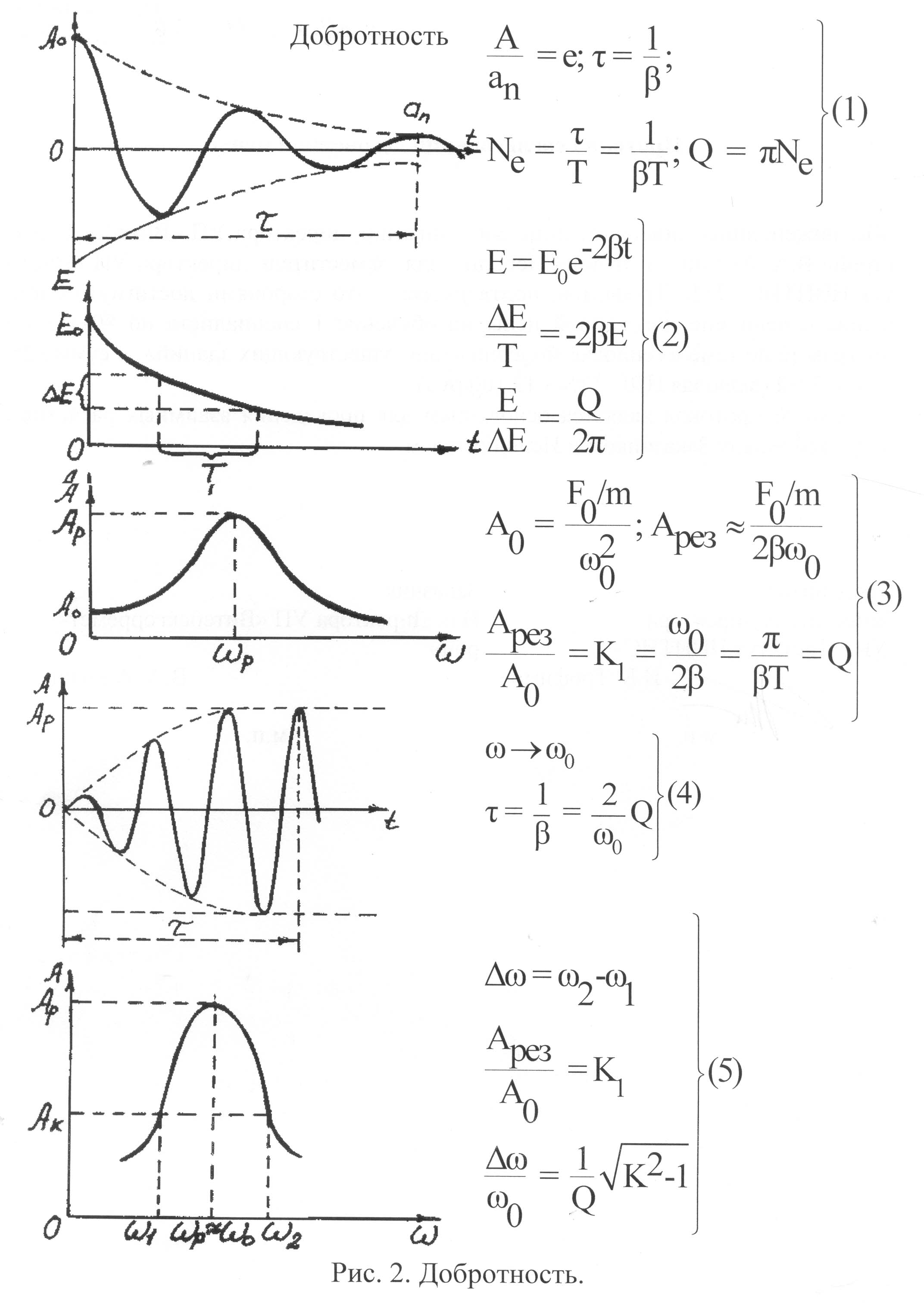
Рис. 24. Добротность как характеристика различных сторон колебательных процессов

Эти данные могут быть использованы при рассмотрении соответствующих осцилляторов.

При рассмотрении добротности колебаний следует уяснить ее роль в процессе затухания амплитуды колебаний, в потере энергии при затухании колебаний, установить ее связь с шириной частотной полосы колебательного контура по заданному уровню, с продолжительностью установления колебаний, а также с коэффициентом усиления колебаний и воспроизводимостью модуляции при усилении модулированного колебания.

Рассмотренные затухающие колебания характеризуются двумя параметрами β и ω (или ω₀). В ряде случаев весьма информативным оказывается их отношение ω/β, называемое добротностью. Аналогично вводится логарифмический декремент затухания. В различных разделах физики и техники определение добротности свое и на это следует обращать внимание. Характеристика различных аспектов колебательных процессов с помощью понятия добротности представлена в таблице 3.

При выполнении работы предполагается, что учащиеся не владеют методами решения дифференциальных уравнений второго порядка. Однако они должны уметь анализировать готовые решения. В приведенной таблице 4 представлены основные колебательные уравнения и их решения. Дифференцированием следует убедиться, что данное решение действительно удовлетворяет указанному уравнению.

Таблица 4

Основные колебательные уравнения и их решения

Гармонические колебания
х 11 + ω02х = 0	x(t) = Acos(ω0 t - 0)
Гармонические колебания около смещенного положения устойчивого равновесия. Реализуются, когда на колеблющуюся материальную точку действует постоянная внешняя сила
х 11 + ω02х = fc	x(t) = х0 + Acos(ω0 t - 0)
Гармонические колебания при силе сопротивления пропорциональной скорости
х11 + 2βх1 + ω02х = 0 (β < ω0)	x(t) = A0e-βt cos(ωt + 0). ω2= ω20 – β2
Гармонические колебания при силе сопротивления пропорциональной скорости и при действии постоянной силы
х11 + 2βх1 + ω02х = fc (β < ω0)	x(t) = х0 + A0e-βt cos(ωt + 0). ω2= ω20 – β2
Гармонические колебания при постоянно действующей внешней силе, которая линейно зависит от времени t.
х11 + 2βх1 + ω02х = a + bt	x(t) = A0e-βt cos(ωt + 0)+α+γt, где ω2= ω20 – β2, γ = b/ ω02, α = a/ ω02 - 2 β b/ ω04
Колебания под действием внешней гармонической силы. Решение в виде установившихся колебаний
х11 + 2βх1 + ω02х = f0 cosωt	x(t) = А cos(ωt - ), где A= f0/( ), tg  = 2βω/(ω02 – ω2).
х11 + ω02х = f0 sinωt	x(t) =
Колебания под действием внешней силы, представимой в виде ряда Фурье. Решение в виде установившихся колебаний
х11 + 2βх1 + ω02х = = f0i cosωi t	x(t) = Аi cos(ωi t - i ), где Ai= f0i /( ), tg i = 2βωi /(ω02 – ωi 2).
Вынужденные колебания в нелинейной системе
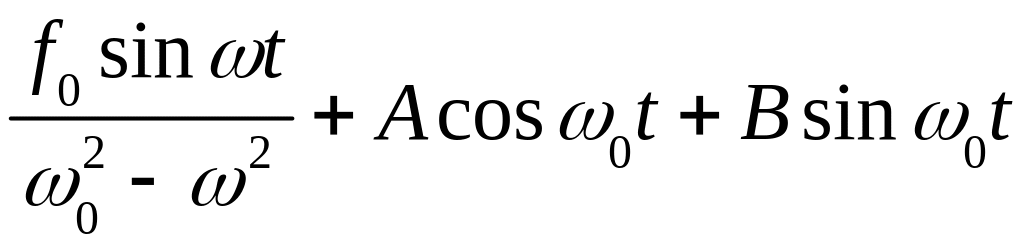
х11 + ω02х +sx3 = f0 cosωt	x(t) ≈ 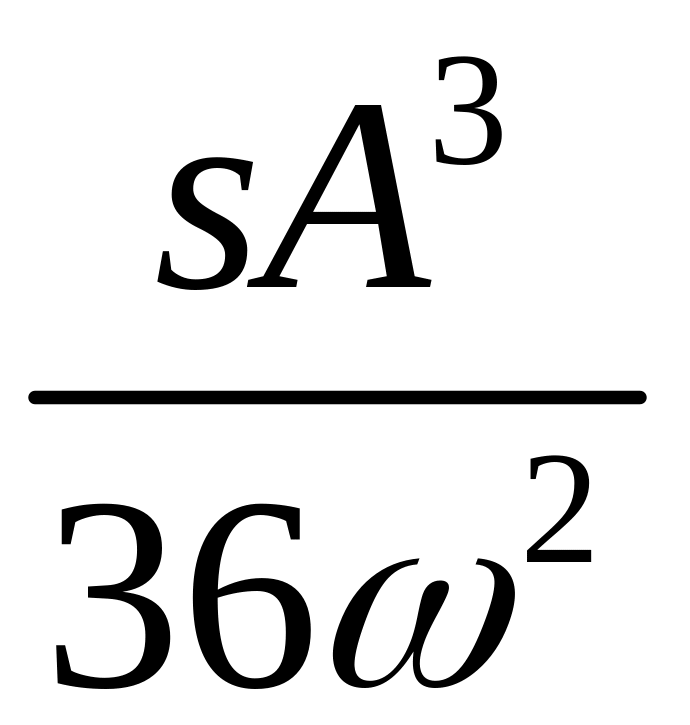( ω02A + sA3 - f0 ) cosωt + cos3ωt. ( ω02)