
- •Физика колебательных процессов
- •Часть 2
- •2.1.21. Параметрические колебания. Параметрический резонанс
- •2.1.22. Автоколебания
- •2.1.23. Режимы работы осциллятора при подводе к нему энергии. Маятник Фруда и ламповый генератор
- •Второй закон Ньютона для вращательного движения имеет вид:
- •1 Случай.
- •2 Случай.
- •2.1.24. Колебания со многими степенями свободы
- •2.1.25. Колебания связанных осцилляторов
- •3. Вспомогательные материалы
- •3.1. Перечень тем курсовых работ по физике
- •3. 2. Указания к выполнению курсового проекта (работы)
- •Пример выполнения работы
- •3.4. Приборы и стенды для выполнения курсовой работы
- •3.5. Заключительные замечания
- •Рекомендуемая литература
- •51. В.А.Касьянов, э.В.Лузик, к.Ф.Войцеховская, с.Г.Ефремов. Рас
- •Кафедра естественнонаучных дисциплин
МИНИСТЕРСТВО ТРАНСПОРТА И КОММУНИКАЦИЙ
РЕСПУБЛИКИ БЕЛАРУСЬ
Департамент по авиации
Минский государственный высший авиационный колледж
Физика колебательных процессов
Часть 2
Методические указания
по выполнению курсовой работы
для студентов дневной и заочной форм обучения
по авиационным специальностям
Минск - 2008 г.
УДК 53 075.32
ББК 22.3я722
Ф 50
Автор
А.И.КИРИЛЕНКО
кандидат физико-математических наук, доцент
Издание второе, переработанное и дополненное
Рецензенты:
Заведующий лабораторией НИИ прикладных физических проблем им. А.Н.Севченко Белгосуниверситета доктор физико-математических наук, профессор В.К.Гончаров и доктор физико-математических наук В. И. Попечиц
Одобрено и рекомендовано к изданию научно-методическим советом МГВАК (протокол № 6 от 15 февраля 2008 г.)
Пособие содержит общие требования и краткие методические указания по выполнению работ, перечень тем курсовых работ, список рекомендуемой литературы. Пособие предназначено для студентов стационара и заочной формы обучения по авиационным специальностям.
Разбиение пособия на две части связано с техническими причинами.
©МГВАК, 2002
©МГВАК, 2008
2.1.21. Параметрические колебания. Параметрический резонанс
На колебательную систему внешние силы могут воздействовать двояким образом. Во-первых, к ней может быть приложена дополнительная внешняя сила. В электрических цепях это соответствует введению в контур вынуждающей ЭДС или введению заданного тока в какой-либо элемент цепи. Во-вторых, внешней силой может изменяться один из параметров системы. Такой вид воздействия называется параметрическим.
 Рассмотрим
одномерную систему, т.е. систему с одной
степенью свободы и ограничимся случаем
периодической модуляции параметра.
Рассмотрим
одномерную систему, т.е. систему с одной
степенью свободы и ограничимся случаем
периодической модуляции параметра.
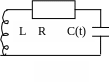
Рис. 42. Колебательный контур с электроемкостью зависящей от вре
мени.
Возьмем линейный колебательный контур (рис. 42), состоящий из последовательно соединенных резонатора, индуктивности и емкости (R,L,C). Пусть емкость конденсатора в контуре меняется во времени с помощью внешнего механического устройства так, что имеет вид, представленный на рис.43.
Предположим,
что изменения емкости малы и заряд на
конденсаторе изменяется по закону
близкому к гармоническому. Если емкость
меняется скачком на 2ΔС
причем уменьшается, то энергия конденсатора
при каждом скачке увеличивается (![]() ).
Заряд q при
скачкообразном изменении емкости не
изменяется, т. к. является инерционной
величиной. Возможно так подобрать
частотные и фазовые соотношения между
q(t)
и С(t),
чтобы емкость конденсатора уменьшалась
каждый раз точно в те моменты, когда
заряд на конденсаторе достигает
минимальной или максимальной величины
(рис.43).
).
Заряд q при
скачкообразном изменении емкости не
изменяется, т. к. является инерционной
величиной. Возможно так подобрать
частотные и фазовые соотношения между
q(t)
и С(t),
чтобы емкость конденсатора уменьшалась
каждый раз точно в те моменты, когда
заряд на конденсаторе достигает
минимальной или максимальной величины
(рис.43).
При этом поступление энергии в систему будет максимальным, т. к. при раздвижении обкладок конденсатора для уменьшения емкости совершается максимальная работа против электростатических сил притяжения между его пластинами.
Как видно из рис.43, частота изменения параметра (емкости) в нашем случае в два раза выше частоты колебаний в контуре.
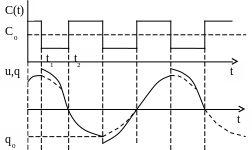
Рис. 43. Изменения емкости, напряжения и заряда на ней в зави
симости от времени.
Рассмотрим приращение электростатической энергии конденсатора ΔW, которое получается в момент скачка емкости
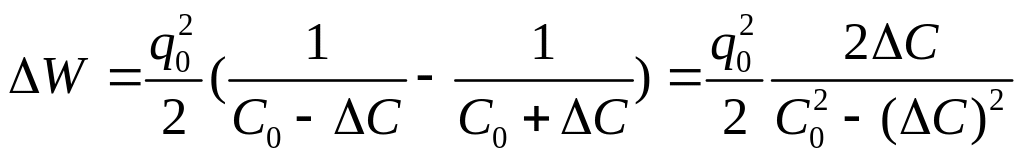 .
.
Здесь q0 - максимальный заряд (по модулю) на конденсаторе при обычном колебательном режиме; кроме того, мы считаем ΔС < < С0 . Поэтому
 .
.
Здесь W0 – энергия, запасенная в конденсаторе до скачка емкости:
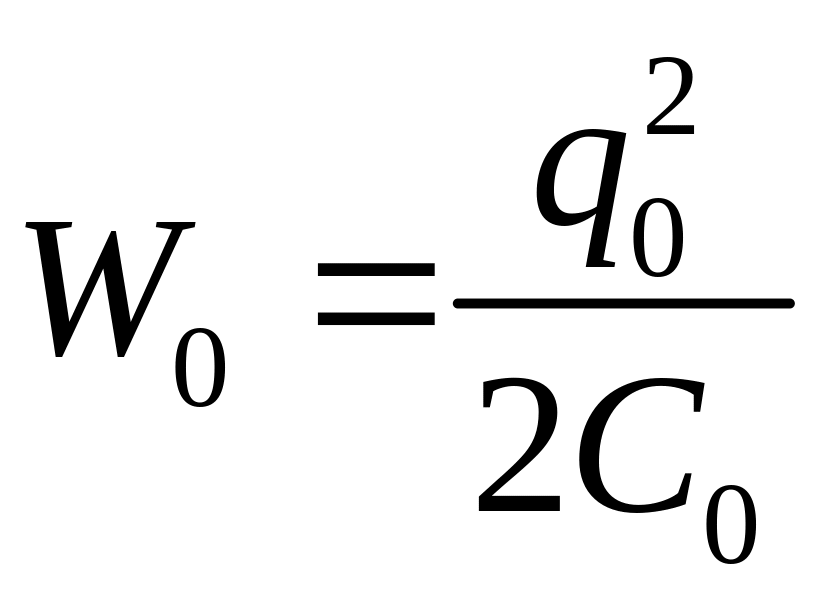 .
.
Введем коэффициент m, называемый глубиной модуляции параметра
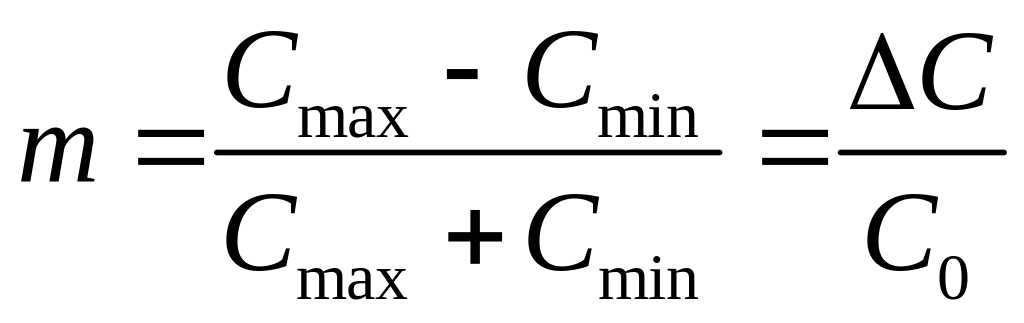 .
.
Через этот параметр приращение энергии колебаний в контуре запишется в виде:
ΔW = W0 · 2m . (133)
Это соотношение является достаточно общим. Оно справедливо и для механических колебательных систем (человек приседает и встает на качелях). Оно выражает простой закон параметрической накачки энергии: величина изменения энергии колебаний пропорциональна величине энергии запасенной в контуре.
В соответствии с выбранным фазовым соотношением между накачкой и колебанием, совершаемым в контуре, скачкообразное увеличение емкости в момент времени, аналогично с t2 на рис. 43, не вызывают изменения энергии в системе, т. к. происходят в такие моменты времени, когда заряд на пластинах конденсатора равен нулю. За один период колебания энергия вкладывается в колебания два раза, строго говоря, неодинаковыми порциями ΔW, однако при ΔC << C0 эта порция отличается мало и общее приращение энергии колебаний за период составит
 .
(134) Рассмотрим потери в
контуре. Будем считать колебания заряда
конденсатора приближенно гармоническими:
q = q0sin
ω0t;
.
(134) Рассмотрим потери в
контуре. Будем считать колебания заряда
конденсатора приближенно гармоническими:
q = q0sin
ω0t;
тогда сила тока в контуре и мощность потерь на активном сопротивлении контура R составит Q = I2R. После усреднения по периоду колебаний, учитывая, что среднее значение величины y = cos2x за период равно
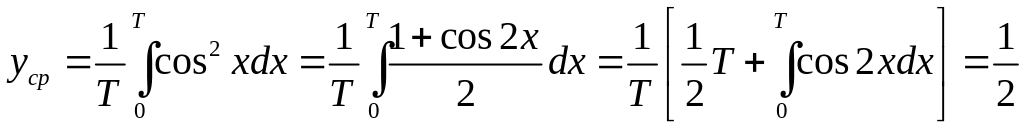 ,
,
будем
иметь
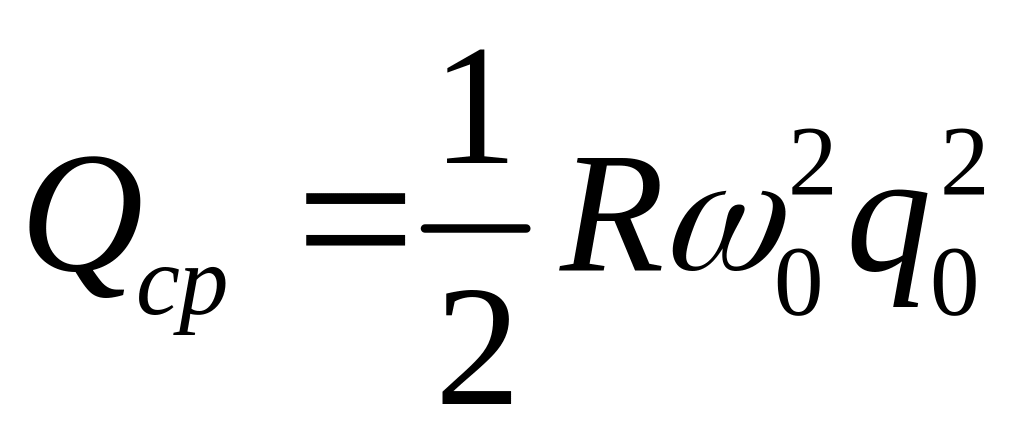 .
.
Энергия, теряемая за период колебаний,
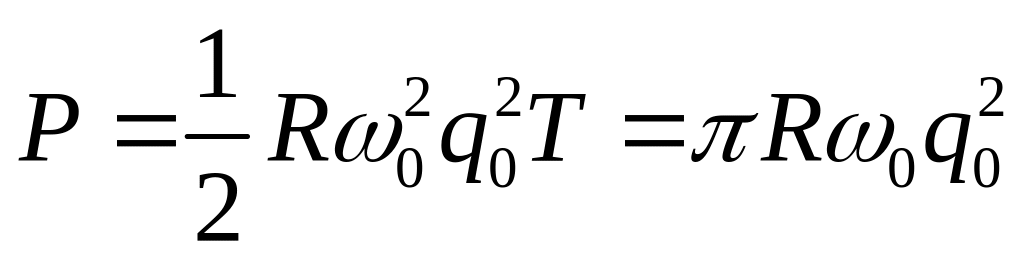 .
(135)
.
(135)
Сравнивая выражения (134) и (135), получим условие, при выполнении которого поступающая энергия превосходит потери и в системе происходит нарастание колебаний
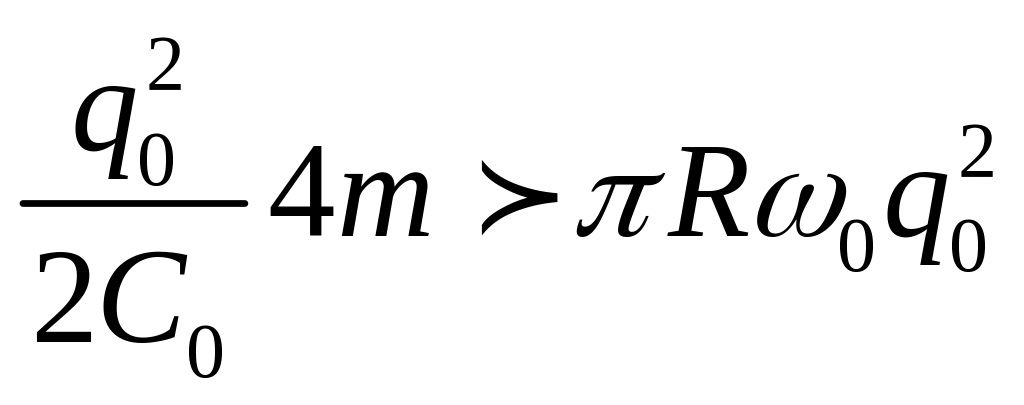 ;
;
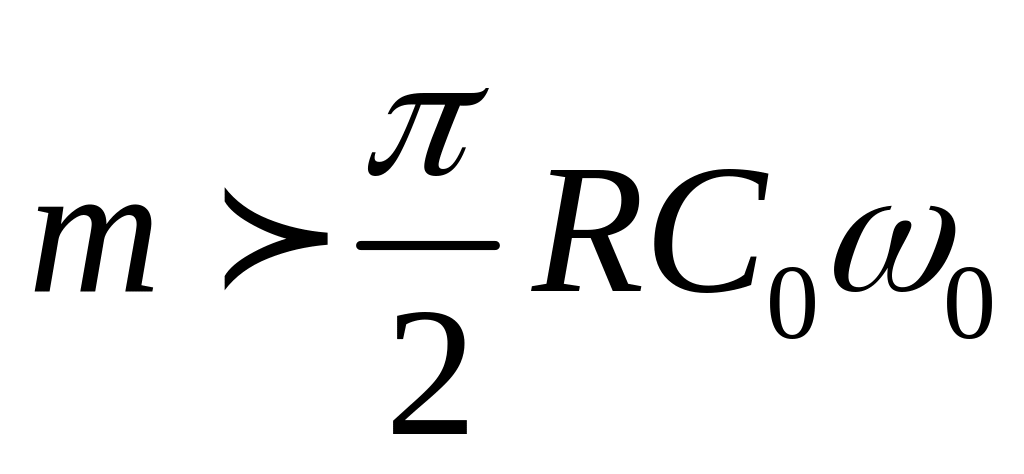 , (136)
, (136)
или
в другом виде m
> m
порог
=
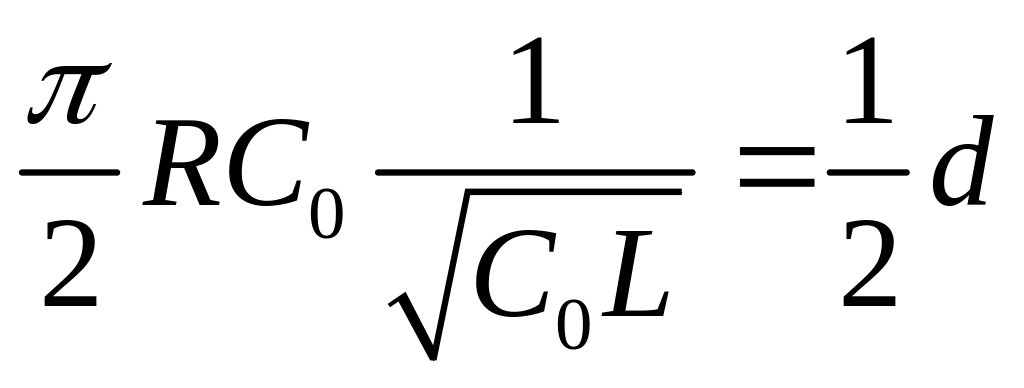 ,
,
где

логарифмический декремент затухания контура.
Такой процесс возбуждения колебания энергоемкого параметра колебательной системы мы назовем параметрическим возбуждением колебаний или параметрическим резонансом.
Если
емкость менять с тем же периодом, но по
другому закону, то получим тот же
результат, но коэффициент в (136) будет
отличен от
![]() и меньше его, т.к в рассматриваемом
случае мы выбрали самый оптимальный
способ сообщения энергии системе.
Понятно, что нарастание колебаний в
контуре и увеличение энергии этих
колебаний происходит за счет работы
внешних сил, изменяющих параметр.
и меньше его, т.к в рассматриваемом
случае мы выбрали самый оптимальный
способ сообщения энергии системе.
Понятно, что нарастание колебаний в
контуре и увеличение энергии этих
колебаний происходит за счет работы
внешних сил, изменяющих параметр.
В данном примере мы меняли параметр дважды за период собственных колебаний системы. Однако можно сообщать энергию системе за счет изменений параметра один раз за период, 2 раза за 3 периода и т.д. Если частота изменения параметра р, а ω0 - частота возбуждения колебаний, то энергия будет поступать в систему при условии
р
=
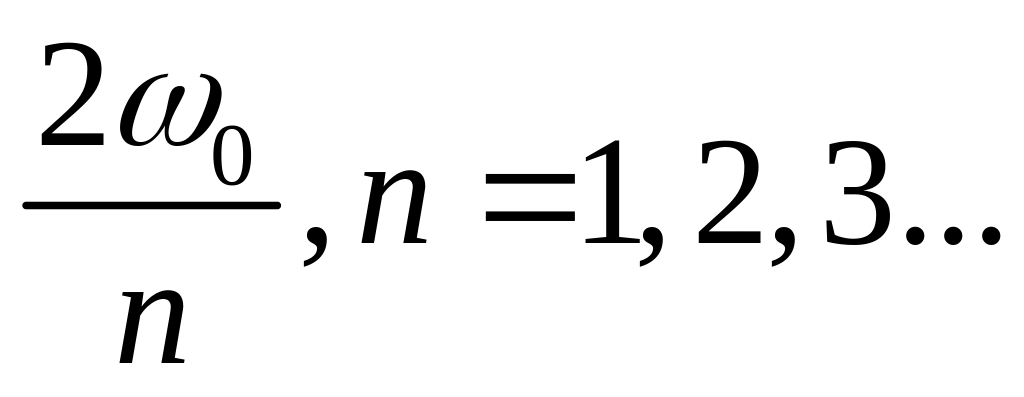 (137)
(137)
Конечно, передача энергии в возбуждаемую систему в течение периода её колебаний тем меньше, чем больше n.
В
электрической цепи энергоемким элементом
является наряду с емкостью и индуктивность
L.
Меняя её скачком в те моменты, когда ток
максимален, мы получим те же результаты.
Анализ удобно проводить, используя
магнитный поток Ф,
поскольку при изменении L
изменяется
I,
но Ф = LI
остаётся неизменным. Поэтому для энергии
удобнее использовать выражение
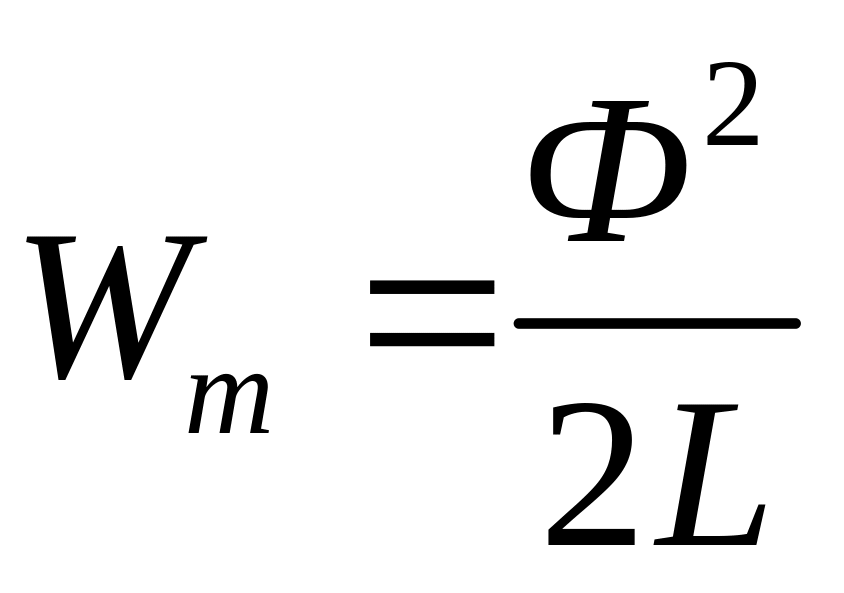 .
Аналогично
.
Аналогично
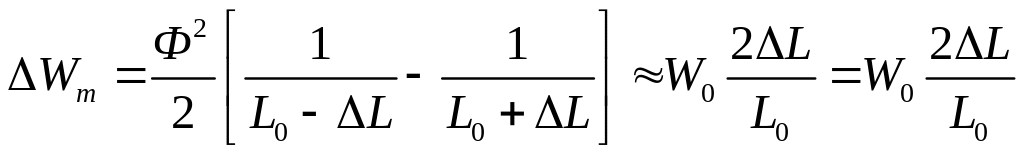 =
=
![]() ,
,
где
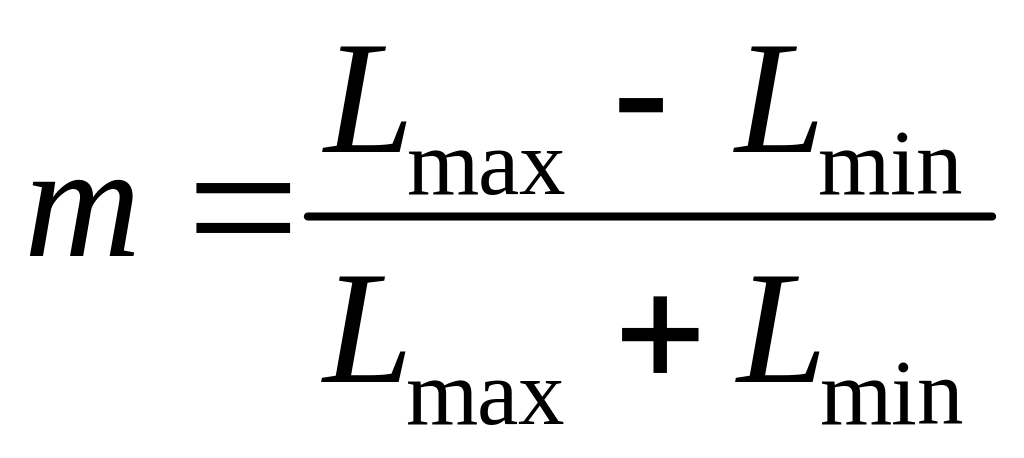 ,
,
![]()
![]() .
.
В проведенном анализе линейной колебательной системы и потери, и прирост энергии колебаний пропорциональны энергии колебаний, т.е. квадрату их амплитуды. При этом происходит неограниченное нарастание амплитуды возбуждаемых колебаний (рис. 44). В линейных системах при внешнем силовом воздействии передача энергии пропорциональна первой степени амплитуды, а потери – квадрату амплитуды. В результате устанавливается конечная амплитуда вынужденных колебаний.
Отметим, что сопротивление в цепи не является энергоемким элементом, поэтому изменение параметра R не приводит к параметрическому возбуждению колебаний.
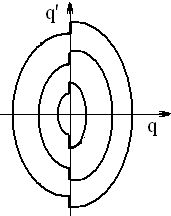
Рис. 44. Примерный вид фазовых траекторий параметрических
колебаний с различными амплитудами
Вывод: параметрический резонанс имеет место при выполнении определенных соотношений между частотой изменения параметра p (137) и частотой возбуждаемых колебаний, причем последняя близка или совпадает с собственной частотой возбуждаемой системы ώ0 . Необходимо также выполнение условий (136), налагаемых на изменения параметра при заданном соотношении частот.
Дадим более строгое математическое описание процесса параметрических колебаний. Параметрический резонанс в линейных системах с одной степенью свободы описывается линейным дифференциальным уравнением с переменными коэффициентами
![]() ,
(138)
,
(138)
где
![]() и
и
![]() периодические
функции времени. Подстановкой
периодические
функции времени. Подстановкой
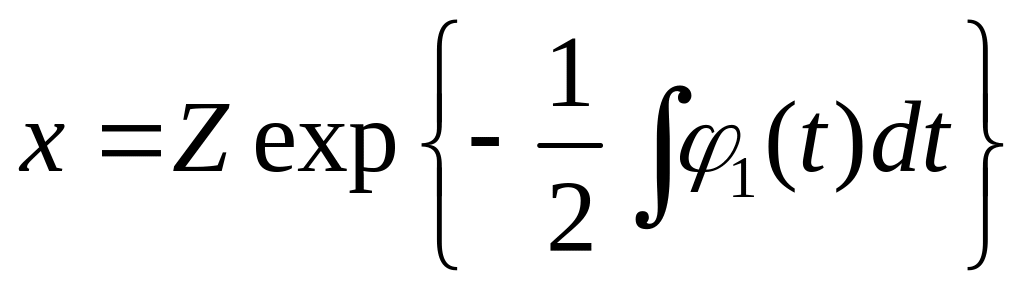
это уравнение преобразуется к стандартному уравнению Хилла
![]() ,
где
,
где

периодическая функция. Частным случаем уравнения Хилла является уравнение Матье
![]() .
(139)
.
(139)
Решение этого уравнения ищут в виде
![]() ,
,
где χ(t) – ограниченные функции с периодом, равным периоду изменения параметра или с половиной этого периода; λ - комплексный характеристический показатель, вещественная часть которого определяет, имеет ли решение нарастающий или убывающий характер.
Пример. Пусть в системе с L и C индуктивность изменяется со времени по закону
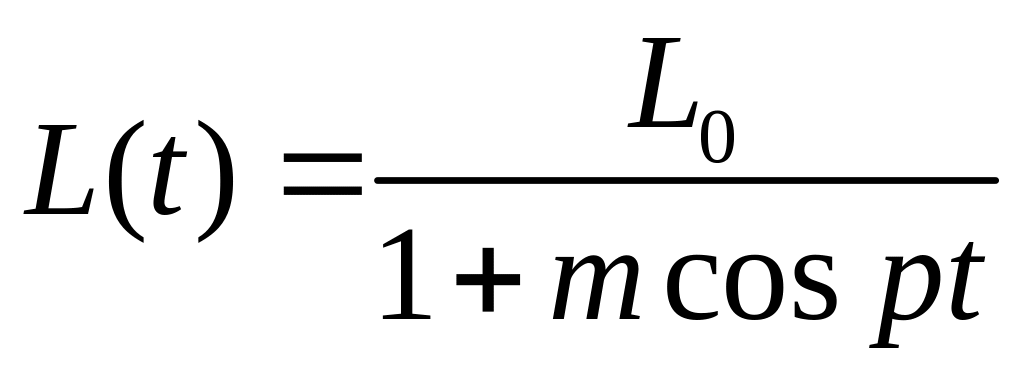
Тогда уравнение, описывающее колебания в системе при p = 2ω, примет вид
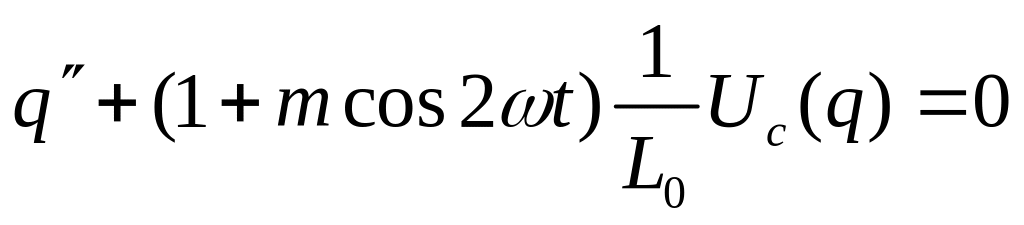
Пусть,
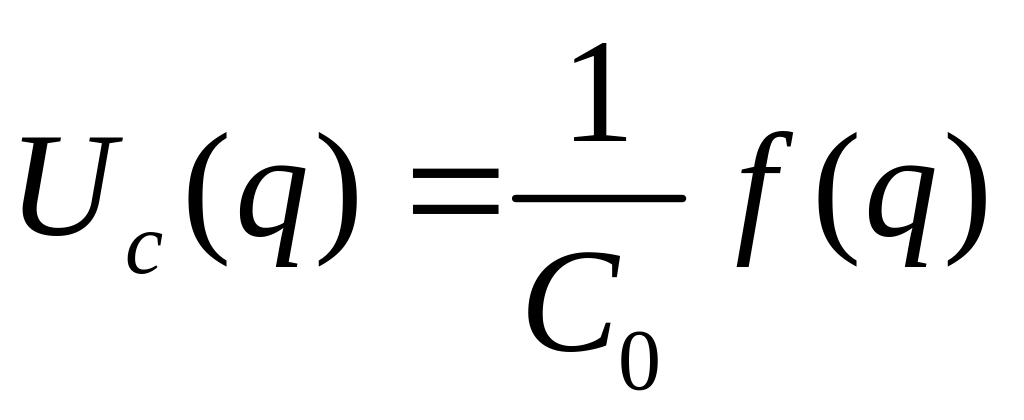 .
.
Тогда
![]() ,
(140)
,
(140)
где
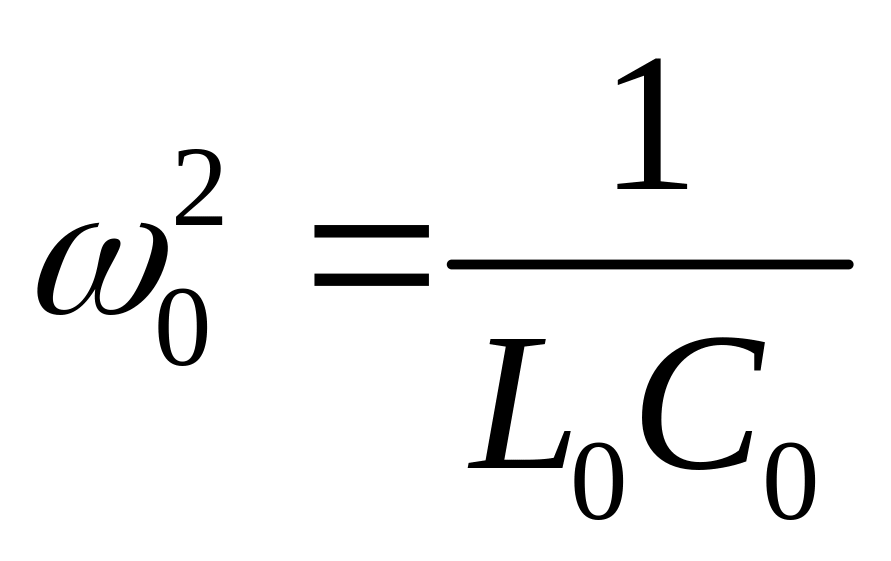 ,
,
![]() -
функция, описывающая нелинейную
характеристику конденсатора.
-
функция, описывающая нелинейную
характеристику конденсатора.
Будем
искать решение уравнения (140) в виде
![]() .
(141)
.
(141)
Продифференцируем (141) и подставим в (140). Получим
 .
(142)
.
(142)
Разложим
функцию
![]() (t)
в ряд Фурье с удержанием членов с
(t)
в ряд Фурье с удержанием членов с
![]() и
и![]() .
Коэффициенты этого разложения α1
и β1 находятся
по формулам
.
Коэффициенты этого разложения α1
и β1 находятся
по формулам
 ,
,
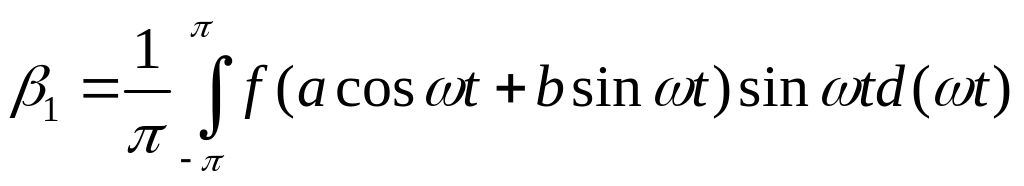 .
(143)
.
(143)
Тогда из (142) имеем
 ;
;
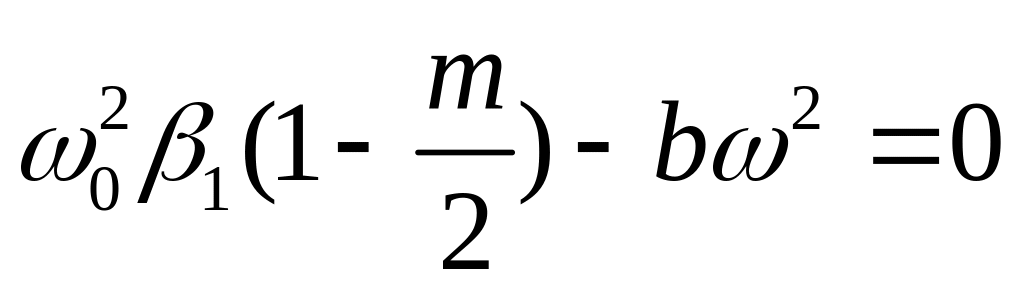 .
(144)
.
(144)
Из этих уравнений находятся a и b, а через них - амплитуда A и фаза δ стационарного решения
![]() ;
;
 .
.
Конкретизируя
результат, выберем нелинейную
характеристику емкости в виде
![]()
![]() .
.
Тогда вычисление интегралов (143) дает:
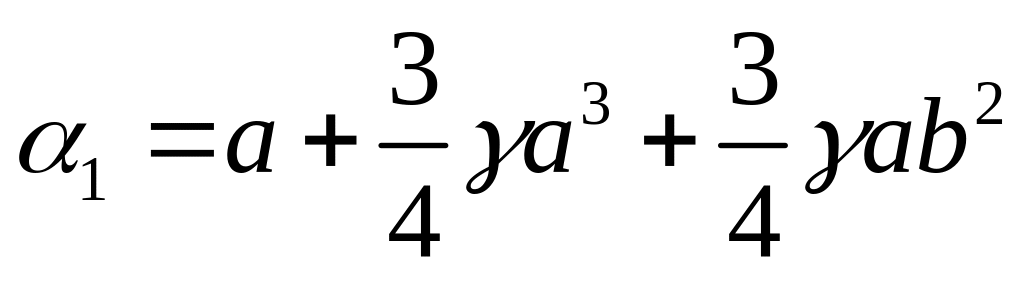 ;
;
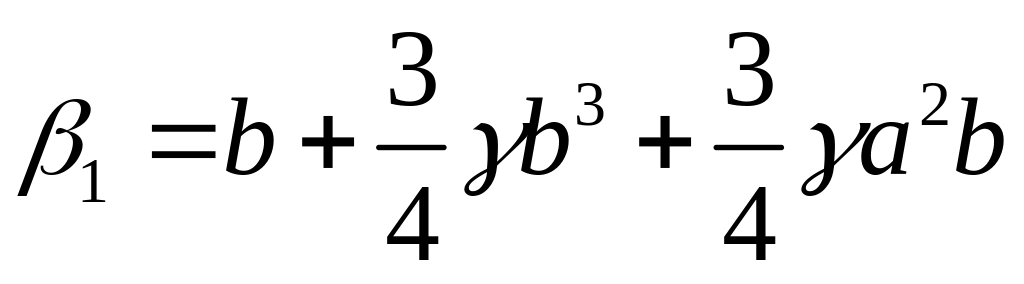 ,
,
а уравнения (144) принимают вид:
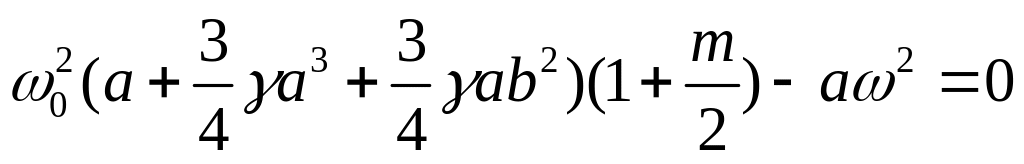 ,
,
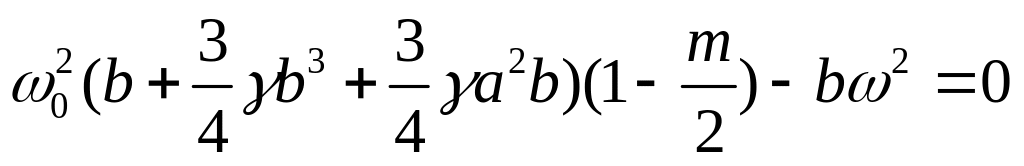 .
.
Эти выражения можно упростить и привести к виду:
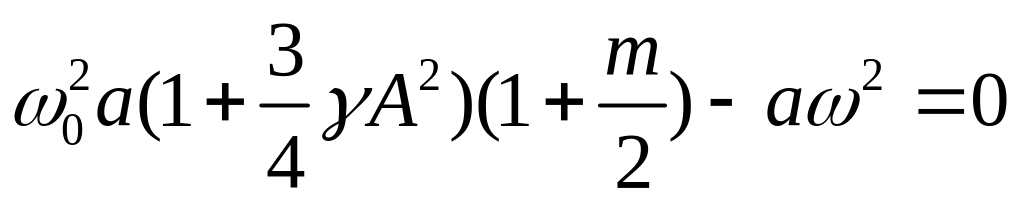 ,
,
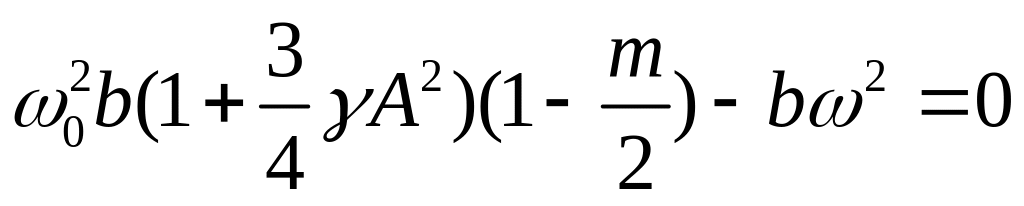 ,
(145)
,
(145)
где
![]()
Данная система допускает решение a = b = A = 0. Как бы мы не изменяли длину подвеса маятника, когда он находится в состоянии покоя (равновесия), колебания в системе не возникнут. То же самое и в электрическом колебательном контуре.
Система (145) имеет решение при a ≠ 0, b ≠ 0 тогда, когда
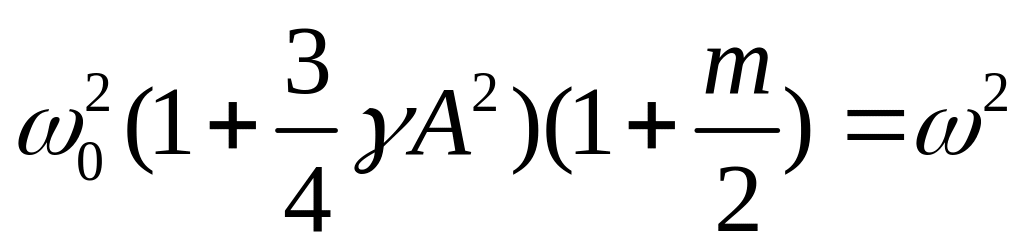 .
.
Отсюда
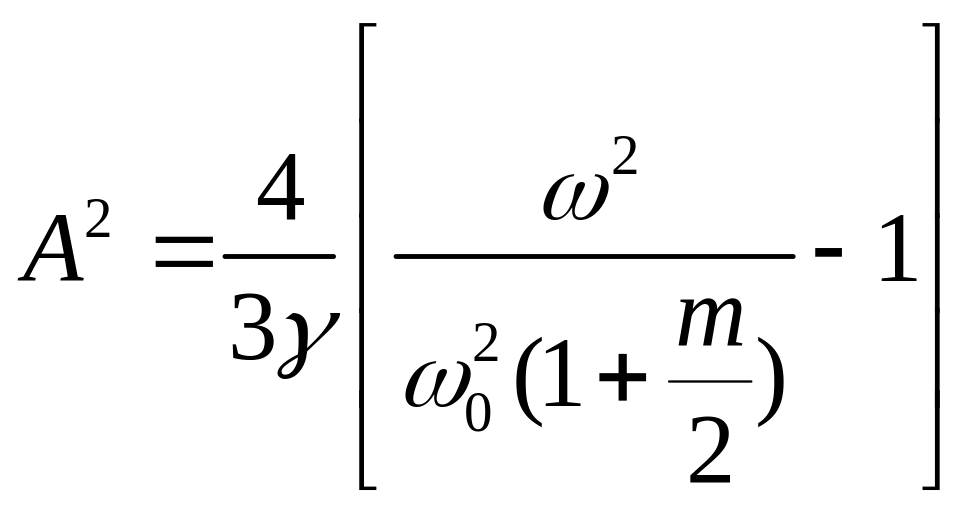 (146)
(146)
Значение
A
тем больше, чем меньше γ – коэффициент
нелинейности систем. Выражение (146) верно
при
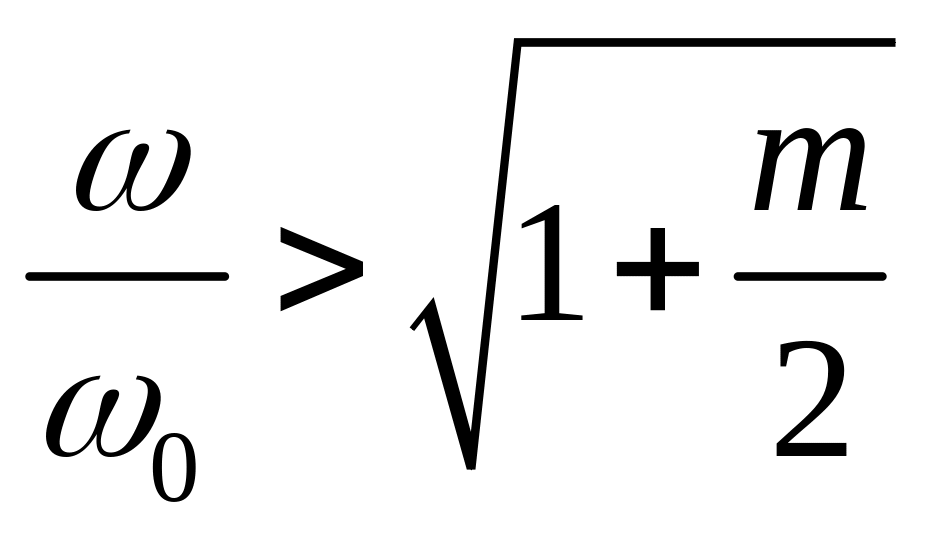 .
.
