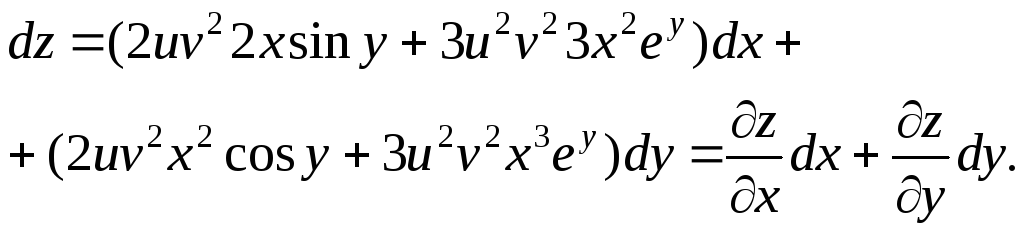Предположим, что в уравнении

z = F(u, v) (22)

и и v являются функциями независимых переменных х и у:

и = (х, у), v = (х, у). (23)

В этом случае z есть сложная функция от аргументов х и у.

Конечно, z можно выразить и непосредственно через х и у, а именно:

z = F((х, у), (х, у)) (24)

Пример 20. Пусть z = u³v³ + u + 1, u = x² + y², v = e^x+y + 1, тогда

z = (х² + у²)³(е^х+у + 1)³ +(х² + у²) + 1.

Предположим, что функции F(u, v), (х, у), (х, у) имеют непрерывные частные производные по всем аргументам и поставим задачу: вычислить ,, исходя из уравнений (22) и (23) и не используя уравнение (24).

Дадим аргументу х приращение х, сохраняя значение у неизменным. Тогда в силу уравнения (23) u и v получат приращения и.

Но если u и v получают приращения и, то и функцияz = F(u, v) получит приращение z, определяемое формулой (12):

.

Разделим все члены этого равенства на х:

.

Если х  0, то  0 и  0 (в силу непрерывности функций u и v). Но тогда ₁ и ₂ тоже стремятся к кулю. Переходя к пределу при х  0, получим

, ,,,

и, следовательно,

. (25)

Если бы мы дали приращение у переменной у, а х оставили неизменным, то с помощью аналогичных рассуждений нашли бы

. (26)

Пример 21. ,,.

, ,,,,.

Используя формулы (25) и (26), находим

,

.

В последнем выражении вместо u и v необходимо подставить исоответственно.

Для случая большего числа переменных формулы (25) и (26) естественным образом обобщаются.

Например, если w = F(z, u, v, s) есть функция четырех аргументов z, u, v, s, а каждый из них зависит от х и у, то формулы (25) и (26) принимают вид

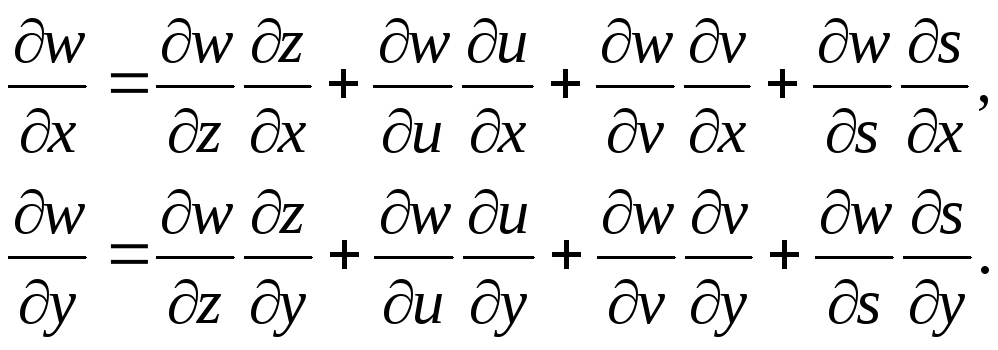(27)

Если задана функция z = F(x, y, u, v), где y, u, v в свою очередь зависят от одного аргумента х:

у = f(x), u = (x), v = (х),

то, по сути дела, z является функцией только одной переменной х и можно ставить вопрос о нахождении производной .

Эта производная вычисляется по первой из формул (27)

;

но так как y, u, v – функции только одного х, то частные производные обращаются в обыкновенные, кроме того, ; поэтому

. (28)

Эта формула носит название формулы для вычисления полной производной (в отличие отчастной производной ).

Пример 22. ,.

, ,.

Формула (28) дает в этом случае следующий результат:

.

Найдем далее полный дифференциал сложной функции, определенной равенствами (22) и (23).

Подставляя выражения и, определенные равенствами (25) и (26), в формулу полного дифференциала

. (29)

Получаем

.

Произведем следующее преобразование в правой части:

. (30)

Но

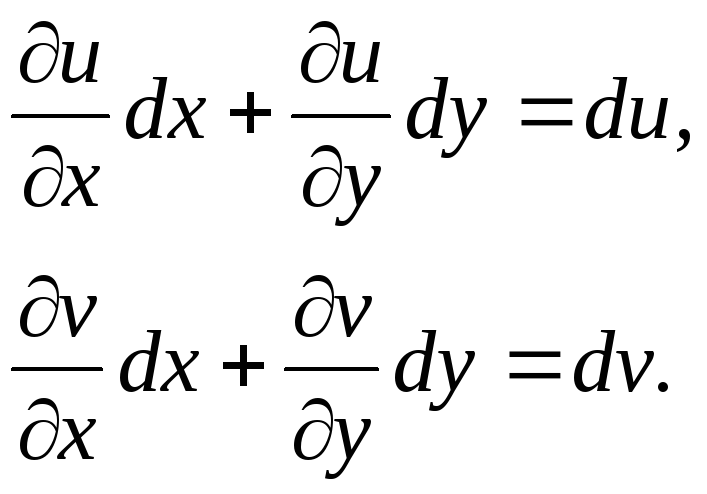(31)

Равенство (30) с учетом равенства (31) можно переписать так:

,

или

. (32)

Сравнивая (29) и (32), можем сказать, что выражение полного дифференциала функции нескольких переменных (дифференциала первого порядка) имеет тот же вид, т.е. форма дифференциала инвариантна, являются ли u и v независимыми переменными или функциями независимых переменных.

Пример 23. Найти полный дифференциал сложной функции

z = u²v³, u = x²sin y, v = x³e^y.

Решение. По формуле (32) имеем

Последнее выражение можно переписать и так: