Задание для самостоятельной работы.

Найти частные и полное приращения функции z:

11. u = x2y3.	12. u = ln(x+y).	13. .
14. .	15. u = arcsin(yx).	16. .
17. .	18. u = xy.	19. .
20. .	21. .	22. .

4. Непрерывность функции нескольких переменных

Введем важное вспомогательное понятие – понятие окрестности данной точки.

Окрестностью радиуса r точки М₀(х₀, у₀) называется совокупность всех точек (х, у), удовлетворяющих неравенству , т.е. совокупность всех точек, лежащих внутри круга радиусаr с центром в точке М₀(х₀, у₀).

Если мы говорим, что функция f(х, у) обладает каким-либо свойством «вблизи точки (х₀, у₀)» или «в окрестности точки (х₀, у₀)», то под этим подразумеваем, что найдется такой круг с центром (х₀, у₀), во всех точках которого данная функция обладает указанным свойством.

Прежде чем рассматривать понятие непрерывности функции нескольких переменных, рассмотрим понятие предела функции нескольких переменных.

Пусть дана функция

z = f(х, у),

о

y

пределенная в некоторой областиG плоскости Оху. Рассмотрим некоторую определенную точку М₀(х₀, у₀), лежащую в области G или на ее границе (рис. 3).

G

М₀(х₀, у₀)

r

М(х, у)

0 x

Рис. 3

Определение 4. Число А называется пределом функции f(х, у) при стремлении М(х, у) к точке М₀(х₀, у₀), если для каждого число   0 найдется такое число r > 0, что для всех точек М(х, у), для которых выполняется неравенство , имеет место неравенство

.

Если число А является предел функции f(х, у) при М(х, у)  М₀(х₀, у₀), то пишут

.

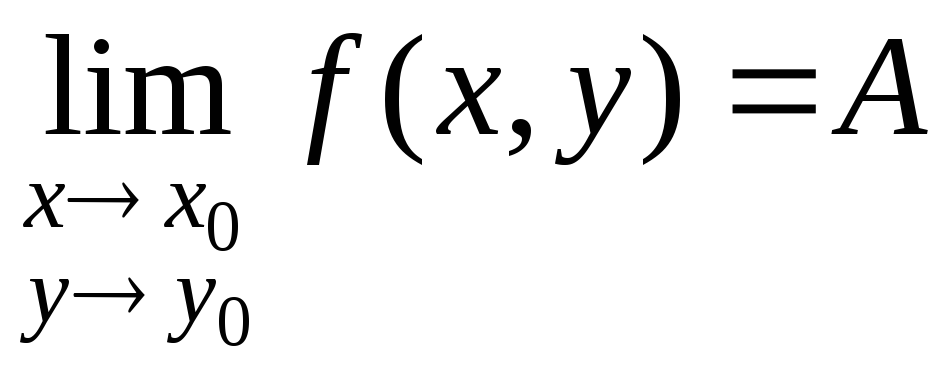Определение 5. Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(х, у). Функция z = f(х, у) называется непрерывной в точке М₀(х₀, у₀), если имеет место равенство

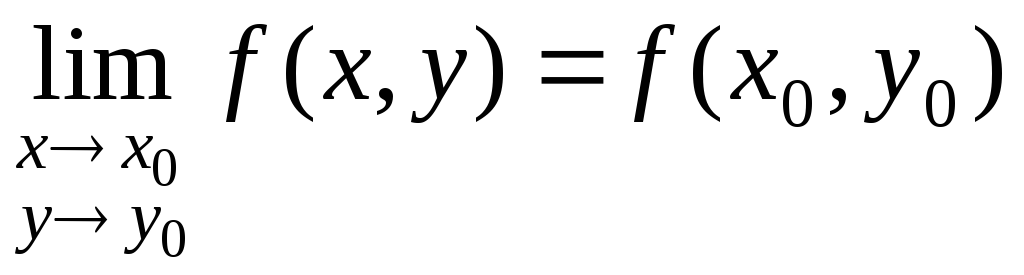, (2)

причем тоска М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом, оставаясь в области определения функции.

Если обозначим х = х₀ + х, у = у₀ + у, то равенство (2) можно переписать так:

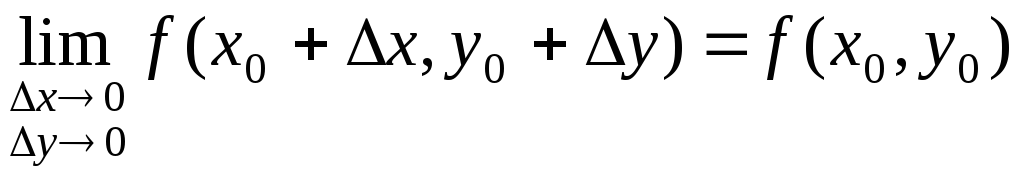(3)

или

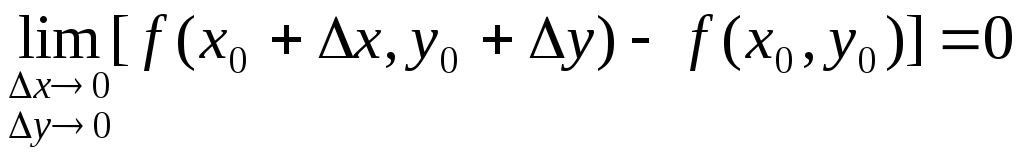. (4)

Обозначим . Прих  0 и у  0   0, и обратно, если   0, то х  0 и у  0.

Замечая, далее, что выражение, стоящее в квадратных скобках в равенстве (4), есть полное приращение функции z, равенство (4) можно переписать в форме

.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.

Если в некоторой точке N(х₀, у₀) не выполняется условие (2), то точка N(х₀, у₀) называется точкой разрыва функции z = f(х, у). Условие (3) может не выполняться, например, в случаях:

1. z = f(х, у) определена во всех точках некоторой окрестности N(х₀, у₀), за исключением самой точки N(х₀, у₀);

2. функция z = f(х, у) определена во всех точках окрестности точки N(х₀, у₀), но не существует предел ;

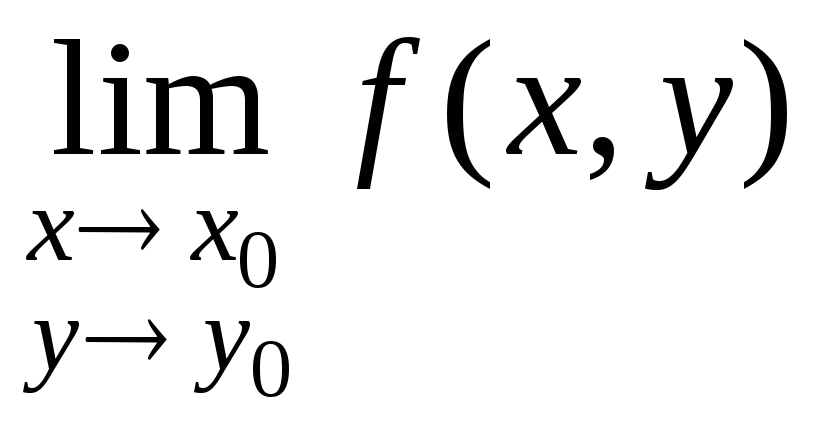3. функция определена во всех точках окрестности N(х₀, у₀) и существует предел 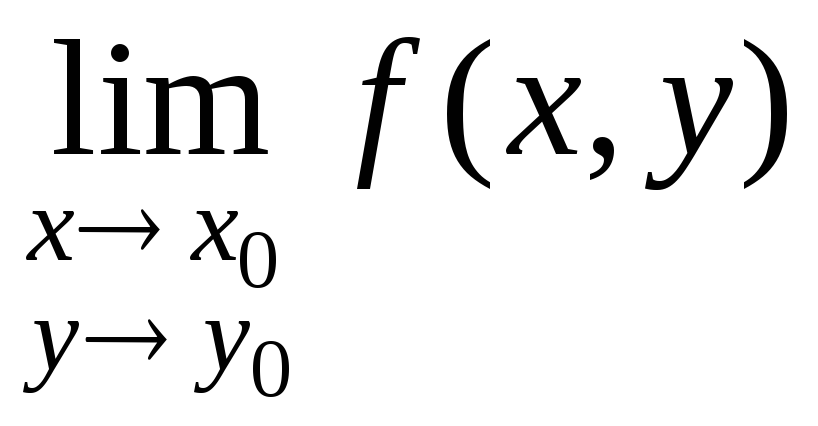, но.

Пример 12. Функция z = х² + у² непрерывна при любых значениях х и у, т.е. в любой точке плоскости Оху.

Действительно, каковы бы ни были числа х и у, х и у, имеем

,

следовательно, .

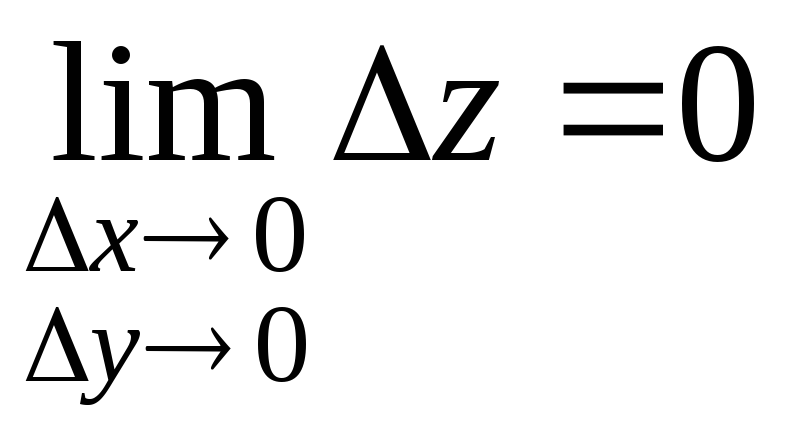Приведем пример разрывной функции.

Пример 13. Функция определена всюду, кроме точких = 0, у = 0.

Рассмотрим значения z вдоль прямой y = kx (k = const). Очевидно, вдоль этой прямой

,

т.е. функция z вдоль всякой прямой, проходящей через начало координат, сохраняет постоянное значение, зависящее от углового коэффициента k прямой. Поэтому, подходя к началу координат по различным путям, мы будем получать различные предельные значения, а это значит, что функция f(х, у) не имеет предела, когда точка (х, у) на плоскости Оху стремится к началу координат. Следовательно, функция разрывна в этой точке. Эту функцию нельзя доопределить в начале координат так, чтобы она стала непрерывной. Легко видеть, с другой стороны, что в остальных точках эта функция непрерывна.

Укажем некоторые важные свойства функции многих переменных, непрерывной в замкнутой и ограниченной области. Эти свойства аналогичны свойствам непрерывной на отрезке функции одной переменной.

Свойство 1. Если функция f(х, у, …) определена и непрерывна в замкнутой и ограниченной области D, то в области D найдется по крайней мере одна точка N(х₀, у₀, …) такая, что для всех других точек области будет выполняться соотношение

f(х₀, у₀, …)  f(х, у, …),

и по крайней мере одна точка Р(х₁, у₁, …) такая, что для всех других точек области будет выполняться соотношение

f(х₁, у₁, …)  f(х, у, …).

Значение функции f(х₀, у₀, …) = М будем называть наибольшим значением функции f(х, у, …) в области D, а значение f(х₁, у₁, …) = т – наименьшим значением.

Это свойство формулируется и так. Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения М и наименьшего значения т.

Свойство 2. Если функция f(х, у, …) непрерывна в замкнутой и ограниченной области D и если М и т – наибольшее и наименьшее значения функции f(х, у, …) в области, то для любого числа , удовлетворяющего условию т <  < М, найдется в области такая точка Р^*(х^*, у^*, …), что будет выполняться равенство f(х^*, у^*, …) = .

Следствие свойства 2. Если функция f(х, у, …) непрерывна в замкнутой ограниченной области и принимает как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых функция f(х, у, …) обращается в нуль.