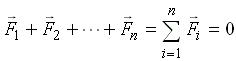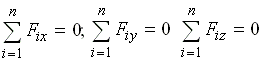Момент
силы относительно центра как векторное
произведение.
Введенного понятия "момент силы
относительно центра как алгебраическая
величина" оказывается недостаточно
в случае сил, произвольно расположенных
в пространстве. Плоскости поворота у
разных сил будут различными и должны
задаваться дополнительно. Удобно ввести
понятие "момент силы относительно
центра как вектор", модуль которого
равен произведению модуля силы на ее
плечо, а направление перпендикулярно
плоскости, проходящей через линию
действия силы и центр момента.
Вектор
момента силы
прикладывают
в центре момента и направляют в сторону,
откуда сила видна вращающей тело в
направлении, противоположном ходу
часовой стрелки (рис. 1.26). Соединим центр
момента О с точкой приложения силы
радиусом-вектором и найдем векторное
произведение
По определению векторного произведения его модуль | |= 2S ОАВ
Модуль
вектора момента силы
также
равен удвоенной площади
ОАВ
=
Направление
векторного произведения также совпадает
с направлением вектора момента.
Следовательно, вектор-момент
силы
относительно
центра О можно рассматривать как
векторное произведение
радиус-вектора
проведенного
из этой точки в точку приложения силы,
на вектор силы
Систе́ма сходя́щихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке.
Такая система сил является на плоскости статически определимой, если число неизвестных сил в ней не больше двух (а не трёх, как в других статически определимых системах). Это обусловлено тем, что у такой системы сил имеется равнодействующая, равная нулю, и её момент равен нулю относительно любой точки плоскости по теореме Вариньона, а не исходя из условий равновесия статики.
В трёхмерном пространстве сходящаяся система сил является статически определимой, если число неизвестных сил в ней не превышает трёх.
На практике простейшим примером сходящейся системы сил являются силы, действующие на груз, лежащий на абсолютно гладком, горизонтальном столе. В такой системе сил имеется сила тяжести, и сила реакции опоры, действующие вдоль одной линии. Другим примером сходящейся системы сил являются силы, действующие в точке подвеса груза, висящего на двух тросах (см. рисунок).
Задачи с системой сходящихся сил могут быть решены как аналитически, так и графически (методами графостатики).
Система сходящихся сил.
Напомним определение системы сходящихся сил. Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.
Используя только аксиомы статики, рассмотрим приведение системы сходящихся сил и найдем условия равновесия твердого тела под действием этой системы сил.
Приведение системы сходящихся сил.
Пусть система сходящихся сил (F1, F2,...,Fn) приложена к твердому телу (рис. 12, a).
Согласно
следствию второй аксиомы, п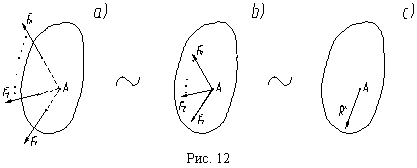
ереносим
все силы системы в точку пересечения
линий действия A и получаем систему
сил, приложенных в одной точке (рис. 12,
b). По аксиоме параллелограмма сил,
начиная с сил F1 и F2,
последовательно складываем силы,
добавляя каждый раз к полученной сумме
по одной силе системы. Дойдя до последней
силы Fn, выясняем, что
система сил (рис. 12, b) эквивалентна одной
силе или равнодействующей R*
(рис. 12, c), равной геометрической сумме
сил системы.
Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:
(F1, F2,...,Fn) ~ R*; R* = F1 + F2 + ... + Fn |
Система сходящихся сил.
Напомним определение системы сходящихся сил. Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.
Используя только аксиомы статики, рассмотрим приведение системы сходящихся сил и найдем условия равновесия твердого тела под действием этой системы сил.
Приведение системы сходящихся сил.
Пусть система сходящихся сил (F1, F2,...,Fn) приложена к твердому телу (рис. 12, a).
Согласно следствию второй аксиомы, п ереносим все силы системы в точку пересечения линий действия A и получаем систему сил, приложенных в одной точке (рис. 12, b). По аксиоме параллелограмма сил, начиная с сил F1 и F2, последовательно складываем силы, добавляя каждый раз к полученной сумме по одной силе системы. Дойдя до последней силы Fn, выясняем, что система сил (рис. 12, b) эквивалентна одной силе или равнодействующей R* (рис. 12, c), равной геометрической сумме сил системы.
Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:
(F1, F2,...,Fn) ~ R*; R* = F1 + F2 + ... + Fn |
(1) |
Условия равновесия системы сходящихся сил.
Эти условия определяют, когда твердое тело находится в равновесии под действием системы сходящихся сил. Сформулируем условие, а затем докажем его.
Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы была равна нулю:
|
(2) |
Необходимость условия сразу следует из (1). При выполнении условия (2) получим R* = 0, следовательно F1, F2,..., Fn ~ 0.
Достаточность условия равновесия докажем методом от противного. Предположим, что условие (2) не выполняется, а твердое тело находится в равновесии. Но если (2) не выполняется, то система сходящихся сил приводится к одной силе, а тело под действием одной силы не может находиться в равновесии. Таким образом, достаточность условия равновесия доказана.
В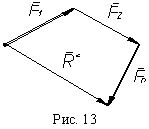
ыражение
(2) представляет собой условие равновесия
в векторной или геометрической
форме. Вспомнив суммирование векторов
по правилу векторного многоугольника
(рис. 13), формулируем условие равновесия
иными словами. На рисунке вектор R*
является суммой векторов и не равен
нулю. Но если R* = 0,
то конец последнего вектора попадет в
начало первого вектора, и векторный
многоугольник, который в нашем случае
можно назвать силовым многоугольником,
окажется замкнутым.
Следовательно, для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник системы был замкнутым.
Применение условия равновесия в геометрической форме ограничено трудностью построения силового многоугольника в пространстве. Более универсальными являются условия равновесия в аналитической форме. Для получения этих условий выберем систему координат OXYZ, связанную с поверхностью Земли . Проектируя на оси координат векторное равенство (2), имеем F1x + F2x +...+ Fnx = 0; F1y + F2y +...+ Fny = 0; F1z + F2z +...+ Fnz = 0. Записав эти выражения в компактной форме, получаем
|
(3) |
По математической записи формулируем условия равновесия в аналитической форме для системы сходящихся сил.
Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил системы на оси координат были равны нулю.
В
плоской системе сходящихся сил все силы
лежат в одной плоскости, например XOY,
и третье условие в (3) вырождается в
тождество
.
Отбрасывая его, имеем условия равновесия
для плоской системы сходящихся сил в
аналитической форме:
|
(4) |
