Заняття 41 Основи теорії алгоритмів

Що таке алгоритм? З давніх часів в математиці склалося інтуїтивне уявлення про алгоритм як формальне розпорядження, яке визначає сукупність операцій і порядок їх виконання для вирішення всіх завдань якого-небудь типа. Кожен зустрічається з алгоритмами з шкільної лави. Правила, по яких виконуються арифметичні дії є простими прикладами алгоритмів. Сам термін «алгоритм» відбувається від імені середньовічного узбецького математика Аль-хорезмі який ще в IX ст сформулювало такі правила.

У своєму розвитку математика накопила величезну кількість різних алгоритмів. Отримуючи відповідну інтерпретацію в конкретних застосуваннях, вони складають значну і найбільш істотну частину математичного апарату1" використовуваного в техніці. У наш час поняття алгоритму піддалося глибокому вивченню і уточненню, головним чином, у зв'язку з проблемою алгоритмічної неразрешимості. Річ у тому, що спроби вирішити ряд завдань натрапили на труднощі, які не удалося здолати, не дивлячись на довгі і наполегливі зусилля багатьох крупних математиків. Наприклад, до цих пір не знайдено алгоритму для вирішення діофантових рівнянь, залишилася нерешенной проблема чотирьох фарб в теорії графів і т. д, У зв'язку з цим виникло припущення, що далеко не для всякого класу завдань можлива побудова вирішуючого алгоритму.

Якщо доказом існування алгоритму служить само опис вирішуючого процесу, то для доказу його відсутність вже недостатньо інтуїтивного поняття алгоритму. Потрібно точно знати, що таке алгоритм і мати в своєму розпорядженні методи строгого доказу алгоритмічної неразрешимості. Ці завдання стали одними з центральних проблем сучасної математики.

2. Чисельні алгоритми.

Алгоритми, які зводять рішення поставленої задачі до арифметичних дій над числами, називаються чисельними алгоритмами. Традиційним прикладом є відомий алгоритм Евкліда для знаходження найбільшого загального дільника двох заданих цілих позитивних чисел а і b. Алгоритм Евкліда складається з наступної системи послідовних вказівок: 1) оглядай а і b переходь до наступного; 2) порівняй числа (а = b, або а < b, або а > b), що оглядають, і переходь до наступного; 3) якщо числа, що оглядають, рівні/то кожне з них дає шуканий результат, якщо немає — переходь до наступного; 4) якщо перше число, що оглядає, менше другого, перестав їх місцями і переходь до наступного; 5) віднімай друге число з першого і оглядай два числа — від'ємник і залишок; переходь до вказівки 2.

Як видно, після п'ятої вказівки слід кожного разу повертатися до другого до тих пір, поки не буде виконано третю вказівку. Хоча заздалегідь і невідомо, скільки буде потрібно таких циклічних переходів, але ясно, що для будь-яких двох чисел мета буде досягнута за кінцеве число кроків. Чисельні алгоритми набули широкою поширення завдяки тому, що до них зводиться вирішення багатьох завдань (обчислення коріння рівнянь алгебри, вирішення систем рівнянь, чисельне диференціювання і інтеграція і т. п.),

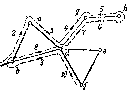
Рис 257. Пошук дороги в лабіринті від крапки а до крапки f .

3, Логічні алгоритми. Існує інший тип алгоритмів, які містять розпорядження, що відносяться не до цифр, а до об'єктів будь-якої природи. Типовим прикладом логічних алгоритмів може служити алгоритм пошуку дороги в кінцевому лабіринті. Лабіринт зручно змальовувати у вигляді графа, вершини якого відповідають майданчикам, а дуги — коридорам (мал. 257). Хай потрібно з'ясувати, чи досяжний майданчик/з майданчика а, і якщо так, то знайти дорогу а в /, а якщо немає — повернутися в а. Звичайно, передбачається, що заздалегідь нічого не відомо про пристрій даного лабіринту. Особа, що шукає дорогу в лабіринті, має в своєму розпорядженні нитку, кінець якої закріплений на майданчику а, і, рухаючись по лабіринту, може розмотувати клубок (Р) або навпаки намотувати на нього нитку (Я). Можна робити відмітки на прохідних коридорах і розрізняти потім коридори ще жодного разу не пройденниє (зелені — 3), пройденниє один раз (жовті — Ж) і пройденниє двічі (червоні — /З). Метод пошуку можете бути заданий наступною схемою: 1) майданчик / — зупинка (мета досягнута); 2) петливши (Я) — намотування нитки (від даного майданчика розходяться, принаймні, два жовті коридори); 3) зелена вулиця (ЗУ) — розмотування нитки (від даного майданчика відходить хоч би один зелений коридор); 4) майданчик а — зупинка (вихідний пункт); 5) відсутність всіх попередніх ознак (ОП) — намотування нитки. Попавши на який-небудь майданчик, звіритися з схемою ознак у вказаному порядку і робити черговий хід відповідно до першої ж виявленої ознаки, не перевіряючи останніх ознак. Такі ходи робляться до тих пір, поки не настане зупинка. Один з можливих варіантів пошуку містить наступні ходи (у скорочених позначеннях вказані номер ходу, ознака, хід, пройденний коридор, колір коридору після його проходження): 1) ЗУ — Р — аb — Ж; 2) ЗУ — р — bо — Ж; 3) ЗУ — Р — cd— — Ж; 4) ЗУ — Р — ае — Ж; б) ЗУ — Р — dg — Ж; 6) ОP — P — gh — Ж 7) ОП — H — hg — К 8) ЗУ — Р — db — Ж; 9) П — H —db — К 10) ЗУ — Р — df — Ж; 11) майданчик f — зупинка. В даному випадку майданчик f виявилася досяжною (недостіжімимі є майданчики i, k, l, т). Виділивши коридори, які залишилися жовтими (аb bз cl, df), отримаємо дорогу від а до f (аbсdf вказаний на мал. 257 жирними дугами). 4, Загальні властивості алгоритмів. Багатий досвід розробки і вживання алгоритмів підказує ряд загальних властивостей, які деталізують приведений вище опис. Дискретність алгоритму. Будь-який алгоритм можна розглядати як процес послідовної побудови величин, що йде в дискретному часі по певному розпорядженню, званому програмою. У початковий момент задається кінцева сукупність величин (вихідні дані), а в кожен наступний момент сукупність величин виходить за програмою з сукупності, що була в попередній момент, Детермінована алгоритму. Сукупність величин', що отримуються в якийсь (не початковий) момент часу, однозначно визначається сукупністю величин, отриманих в попередні моменти часу. Наприклад, алгоритм пошуку дороги в лабіринті допускає свавілля у виборі коридору за наявності декількох зелених коридорів, що відходять від даного майданчика. Аби зробити його строго детермінованим, необхідно додати розпорядження про вибір зеленого коридору (наприклад, перший за годинниковою стрілкою). Спрямованість алгоритму. Якщо спосіб здобуття подальшої величини з якої-небудь заданої не наводить до результату, то має бути вказівка, що треба вважати результатом алгоритму. Інакше кажучи, алгоритм через кінцеве число тактів часу (кроків) повинен привести до зупинки, яка свідчить про досягнення необхідного результату. Так, при пошуку дороги в лабіринті зупинка настає або на досяжному майданчику, або при поверненні на вихідний майданчик, якщо вказана мета недостіжіма. Масовість алгоритму. Алгоритм служить для вирішення цілого класу завдань, причому початкова сукупність величин може вибиратися з деякої безлічі. Наприклад, в алгоритмі Евкліда числа a і b вибираються з безконечної (рахункового) безлічі цілих чисел, а в алгоритмі пошуку дороги в лабіринті початковий і кінцевий майданчики вибираються з кінцевої безлічі майданчиків лабіринту. У математиці проблема вважається вирішеною, якщо для неї знайдений загальний алгоритм. Елементарність кроків алгоритму. Розпорядження про здобуття подальшої сукупності величин з передуючої має бути простим і локальним. Це означає, що відповідна операція має бути елементарною для виконавця алгоритму (людини або машини). Наприклад, операції порівняння, віднімання і перестановки чисел, що зустрічаються в алгоритмі Евкліда, можна було б розчленувати на простіші операції, якби вони не вважалися досить стандартними і звичними. В той же час сам алгоритм Евкліда може фігурувати як елементарна операція складнішого алгоритму. 5. Асоціативне числення. Подальше узагальнення поняття алгоритму пов'язане з асоціативним численням, яке будується на безлічі всіх слів в даному алфавіті. Нагадаємо, що алфавіт є будь-якою кінцевою системою різних символів, званих буквами. Будь-яка кінцева послідовність п букв деякого алфавіту є словом довжини п в цьому алфавіті. Наприклад, в алфавіті з трьох букв {а, b, c}словами будуть послідовності b, ас,bас, аbbcа, сbсссасаbса і так далі Порожнє слово що не містить жодної букви, зазвичай позначається через ^ . Якщо слово L є частиною слова М, то говорять про входження слова L у слово М. Наприклад, в слові аbсbсbаb є два входження слова bсb і одне входження слова bа. Як операції асоціативного числення визначається система допустимих підстановок, за допомогою яких одні слова перетворяться в інших. Підстановка вигляду L—м, де L і М— слова в тому ж алфавіті, означає заміну входження лівій частині правою, так само як і заміну правою частини лівою. Інакше кажучи, якщо в деякому слові R є одне або декілька входжень слова L, то кожне з цих входжень може замінюватися словом М, і навпаки, якщо є входження слова М, то його можна замінити словом L. Наприклад, підстановка аb—bсb застосовна чотирма способами до слова аbсbсbаb. Заміна кожного з двох входжень bсb дасть слова ааbсbаb і аbсаbаb, а заміна кожного з двох входжень аb дає слова bсbсbсbаb, аbсbсbbсb. В той же час до слова bасb ця підстановка не не застосовна. Підстановка вигляду Р—/\ означає, що з перетворюваного слова викидається входження слова Р, а також що між двома якими-небудь буквами перетворюваного слова або попереду нього, або за ним вставляється слово Р. Отже, асоціативне числення — це безліч всіх слів в деякому алфавіті разом з якою-небудь кінцевою системою допустимих підстановок. Вочевидь, аби задати., асоціативне числення, досить визначити алфавіт і систему допустимих підстановок (наприклад, алфавіт (а, b, c d, е) і система підстановок ас—са, аd—dа bс—сb bd—db, аbас—аbасс, еса—аe, еdb—bе).

6. слів. Два слова називаються еквівалентними, якщо одне з них можна отримати з іншого послідовним вживанням допустимих підстановок. Так, в приведеному вище (5) численні еквівалентними є, наприклад, слова аbсdе і саdеdb, що видно з наступних послідовних перетворень: аbсdе, асbdе, саbdе, саdbе, саdеdb. Послідовність слів R1, R2, ..., Rп, коли кожне наступне слово є результатом однократного вживання допустимої підстановки до попереднього слова, утворює дедуктивний ланцюжок, причому сусідні слова в цьому ланцюжку називають суміжними, Вочевидь, будь-які два слова в дедуктивному ланцюжку є еквівалентнимі* Еквівалентність слів L і М позначається L ~М і володіє всіма властивостями відношення еквівалентності (рефлективність, симетричність і транзитивність). Якщо L ~ М, то за наявності в якому-небудь слові R входження L в результаті підстановки L — М виходить слово, еквівалентне R. Наприклад, скориставшись еквівалентністю аbсdе~саdbе, із слова bbаbсdес отримуємо еквівалентне йому слово bbсаdbес. У кожному асоціативному численні виникає своя спеціальна проблема слів, що полягає в наступному: для будь-яких двох слів в даному численні потрібно взнати, еквівалентні вони чи ні. Вирішення цієї проблеми аналогічно пошуку дороги в лабіринті, майданчики якого відповідають суміжним словам. Вочевидь, еквівалентність двох слів означає що відповідні ним майданчики зв'язані деяким дорогою, яка є дедуктивним ланцюжком від одного слова до іншого. Проте проблема слів є узагальненням завдання пошуку дороги, що далеко йде, в кінцевому лабіринті. Оскільки в будь-якому асоціативному численні міститься безконечна безліч різних слів, то відповідний лабіринт має безконечне число майданчиків, і, отже, рішення питання про еквівалентність будь-яких двох слів зводиться до пошуку дороги в безконечному лабіринті. З допомогою алгоритму перебору вирішується обмежена проблема слів: потрібно встановити, чи можна одне із заданих слів перетворити в інше вживанням допустимих підстановок не більш, ніж і раз, де і — довільне, але фіксоване число. Для цього досить побудувати всі слова, суміжні з одним із заданих слів, потім для кожного з отриманих слів побудувати всі слова, суміжні з ним і так далі всього k раз. В результаті отримаємо список всіх слів, які можна отримати з заданого за допомогою допустимих підстановок, вживаних не більш k раз. Якщо друге задане слово виявиться в цьому списку, то відповідь на поставлене питання буде позитивною, а якщо його в списку немає, відповідь негативна. Можна відмітити, що обмежена проблема слів відповідає обмеженню лабіринту таким чином, що відстань між даними майданчиками не перевищує k коридорів. Проте така дорога принципово не придатна для вирішення неограніченной проблеми слів. Оскільки довжина дедуктивного ланцюжка, що тягнеться між еквівалентними словами (якщо такий ланцюжок існує), може виявитися скільки завгодно великою, то не існує жодної можливості вказати таке кінцеве число k, яке гарантує вирішення проблеми шляхом простого перебору. Тому для здобуття бажаних результатів необхідно застосовувати інші ідеї, засновані на аналізі самого механізму перетворення слів за допомогою допустимих підстановок. В деяких випадках можуть бути виявлені і використані властивості, що залишаються незмінними для всіх слів дедуктивного ланцюжка (дедуктивні інваріанти). Так, в кожній з допустимих підстановок числення з (5) ліва і права частини містять одне і те ж число входжень букви а. Отже, в будь-якому дедуктивному ланцюжку всі слова також повинні містити одне і те ж число входжень букви а. На основі цього дедуктивного інваріанта можна встановити, які слова не можуть бути еквівалентними (наприклад, слова аbасdас і аbааdас — не еквівалентні). Проблема слів в асоціативному численні має величезне значення у зв'язку з тим, що до неї зводяться багато геометричних, алгебра і логічні завдань. Так, будь-яку формулу логіки висловів і предикатів можна трактувати як слова в деякому алфавіті, що містить логічні символи, вислови, предикати і наочні змінні. Процес еквівалентного перетворення або виведення логічного слідства може бути представлений як перетворення слів, причому роль допустимих підстановок грають логічні закони або аксіоми. Таким чином, питання про виводимість якої-небудь формули стає питанням існування дедуктивних ланцюжків, ведучих від слів, що представляють посилки, до слів, що представляють слідство. У ряді інтерпретацій асоціативного числення, зокрема в теорії виводу, використовуються орієнтовані підстановки вигляду L®М, які допускають лише підстановку зліва направо (слова L у слово М). Це відповідає лабіринтам, по кожному коридору якого можна рухатися лише в одному напрямів. \

7. Нормальний алгоритм Марков. Система допустимих підстановок в деякому алфавіті, забезпечена точним розпорядженням про порядок і спосіб їх використання, дозволяє здійснити процес, що термінує, який послідовно перетворить деяке слово в нові слова, еквівалентні початковому. Говорять, що заданий алгоритм в алфавіті А, який застосовний до слова L, і переробляє його в словоm, якщо, вирушаючи від L і діючи згідно розпорядженню, врешті-решт отримують М на якому процес обривається. Безліч слів, до яких застосуємо даний алгоритм, називають його областю застосовності. Два алгоритми в деякому алфавіті називаються еквівалентними, якщо області їх застосовності збігаються і результати переробки їх будь-якого слова із загальної області застосовності також збігаються. Важливий крок на дорозі уточнення поняття алгоритму зроблений А. А. Марковом, який дав стандартні раз і назавжди певні вказівки про порядок використання підстановок визначення нормального алгоритму Марков зводиться до следущему. Задається алфавіт А і фіксується у визначеному порядку система орієнтованих підстановок. Виходячи з довільного слова R у алфавіті A, є видимими підстановки в тому порядку, в якому вони задані. Перша підстановка, що зустрілася, з лівою частиною, що входить в R, використовується для перетворення R у яке замість першого входження її лівої частини підставляється її права частина, внаслідок чого отримуємо нове слово R1Далі процес Далі процес повторюється, виходячи із слова R1, R2і так далі до тих пір, поки цей процес не зупиняється. Ознаками зупинки процесу служать два випадки: по-перше, коли виходить таке слово Rn що жодна з лівих частин допустимих підстановок в нього не входять, і по-друге, коли при здобутті Rп доводиться застосовувати останню підстановку. Хай, наприклад, заданий алфавіт А ={1, +} і система підстановок: + ^ , 11 (^ — порожнє слово). Слово 111 + 11 + 1111+ 1 цей алгоритм переробляє так:

111 + 11 + 1111 + 1

11111 + 1111 + 1

111111111 + 1

1111111111

1111111111

Процес закінчується вживанням завершальної підстановки, яка переробляє слово само в себе. Як видимий алгоритм підсумовує кількість одиниць, тобто здійснює операцію складання. Еквівалентний йому алгоритм можна задати за допомогою системи підстановок:. 1 +  + 1; +1 1; 1 1.