Лекції з курсу (електронна версія)

Теорія алгоритмів

Доцент кафедри вищої математики Гаврилов В.Г.

Лекція 1

Основні поняття теорії алгоритмів

Кілька вступних слів. З алгоритмами, тобто ефективними процедурами, що однозначно приводять до результату, математика мала справу завжди. Шкільні методи множення "стовпчиком" і ділення "кутом", метод виключення невідомих при розв'язку системи лінійних рівнянь, правило диференціювання складної функції, спосіб побудови трикутника по трьом заданим сторонам - усе це алгоритми. Однак поки математика мала справу в основному із числами й обчисленнями й поняття алгоритму ототожнювалося з поняттям методу обчислення, потреби у вивченні самого цього поняття не виникало. Традиції організації обчислень складалися століттями й стали складовою частиною загальної наукової культури тією самою мірою , що й елементарні навички логічного мислення. Усе різноманіття обчислень комбінувалося з 10-15 чітко певних операцій арифметики, тригонометрії й аналізу. Тому поняття методу обчислення вважалося споконвічно ясним і не потребувало спеціальних досліджень.

До середини XIX ст. єдиною областю математики, що працювала з нечисловими об'єктами, була геометрія, і саме вона, не маючи можливості опиратися на обчислювальну інтуїцію людини, різко відрізнялася від іншої математики підвищеними вимогами до строгості своїх міркувань. Дотепер будь-який сучасний шестикласник, для якого математика - це світ обчислень (і в цьому він мало чому відрізняється від типового інженера), болісно звикає до понять доказу й математичної побудови й ніяк не може зрозуміти, навіщо доводити рівність відрізків, коли їх простіше виміряти, і навіщо будувати перпендикуляр за допомогою циркуля й лінійки, коли є косинець із "готовим" прямим кутом або транспортир.

Таке ж болісне звикання до нових, більш твердим вимогам строгості почалося в математику в другій половині XIX ст. Воно стимулювалося в основному математикою нечислових об'єктів - відкриттям неевклідових геометрій, появою абстрактних алгебраїчних теорій типу теорії груп і т.д. Одніею з вирішальних обставин, що привела до перегляду підстав математики, тобто принципів, що лежать в основі математичних міркувань, з'явилося створення Кантором теорії множин. Досить швидко стало ясно, що поняття теорії множин у силу своєї спільності лежать в основі всього будинку математики. Однак майже настільки ж швидко було показано, що деякі гадані цілком природніми міркування в рамках цієї теорії приводять до нерозв'язних протиріч - парадоксам теорії множин (які згадувалися в гл. 1; більш докладно див. [42]). Усе це вимагало точного вивчення принципів математичних міркувань (дотепер казавшихся інтуїтивно ясними) математичними ж засобами. Виникла особлива галузь математики - підстави математики, або метаматематіка.

Досвід парадоксів теорії множин навчив математика вкрай обережно поводитися з нескінченністю й по можливості навіть про нескінченність міркувати за допомогою фінітних методів (див. § 3-4). Суть фінітного підходу полягає в тому, що він допускає тільки кінцеві комплекси дій над кінцевим числом об'єктів. З'ясування того, які об'єкти й дії над ними слід уважати точно визначеними, які властивості й можливості мають комбінації елементарних дій, що можна й чого не можна зробити з їхньою допомогою,- усе це стало предметом теорії алгоритмів і формальних систем, которая первоначально утворилася в рамках метаматематики та стала найважливішою її частиною. Головним внутрішнматематичним додатком теорії алгоритмів з'явилися докази неможливості алгоритмічного (тобто точного й однозначного) розв'язку деяких математичних проблем. Такі докази (та й точні формулювання доказуваних тверджень) нездійсненні без точного поняття алгоритму.

Поки техніка використовувала чисто обчислювальні методи, ці високі проблеми чистої математики її мало цікавили. У техніку термін "алгоритм" прийшов разом з кібернетикою. Якщо поняття методу обчислення не потребувало пояснень, то поняття процесу керування довелося виробляти практично заново. Знадобилося усвідомлювати, яким вимогам повинна задовольняти послідовність дій (або її опис), щоб уважатися конструктивно заданої, тобто мати право називатися алгоритмом. У цім усвідомленні величезну допомогу інженерноій інтуїції виявила практика використання обчислювальних машин, що зробила поняття алгоритму відчутною реальністю. З погляду сучасної практики алгоритм - це програма, а критерієм алгоритмичности процесу є можливість його запрограмувати. Саме завдяки цій реальності алгоритму, а також тому, що підхід інженера до математичних методів завжди був конструктивним, поняття алгоритму в техніку за короткий строк стало надзвичайно популярним (можливо , навіть більше, чим у самій математиці).

Однак у всякої популярності є свої витрати. У повсякденній практиці слово "алгоритм" уживається занадто широко, втрачаючи найчастіше свій точний зміст. Приблизні описи поняття "алгоритм" (начебто того, яке наведено в першій фразі цього параграфа) часто ухвалюються за точні визначення. У результаті за алгоритм найчастіше видається будь-яка інструкція, розбита на кроки. З'являються такі дикі словосполучення, як "алгоритм винаходження" (але ж наявність "алгоритму винаходження" означало б кінець винахідництва як творчої діяльності).

Зрозуміле представлення про те, що таке алгоритм, важливо, звичайно, не тільки для правильного слововживання. Воно потрібно й при розробці конкретних алгоритмів, особливо коли мається на увазі їх наступне програмування. Однак воно ще важливіше при наведенні порядку в бурхливо зростаючому алгоритмічному господарстві. Щоб орієнтуватися в морі алгоритмів, що захлиснув технічну кібернетику, необхідно вміти порівнювати різні алгоритми розв'язку тих самих завдань, причому не тільки по якості розв'язку, але й по характеристиках самих алгоритмів (числу дій, витраті пам'яті і т.д.). Таке порівняння неможливе без уведення точної мови для обговорення всіх цих питань; інакше кажучи, самі алгоритми повинні стати такими ж предметами точного дослідження, як і ті об'єкти, для роботи з якими вони призначені.

Строге дослідження основних понять теорії алгоритмів почнеться в наступному параграфі. Перш ніж приступитися до нього, обговоримо на неформальному рівні деякі основні принципи, по яких будуються алгоритми, і з'ясуємо, що ж саме в понятті алгоритму потребує уточнення.

Основні вимоги до алгоритмів. 1. Перше, що слід зазначити в будь-якому алгоритмі, - це те, що він застосовується до вихідних даних і видає результати. У звичних технічних термінах це означає, що алгоритм має входи й виходи. Крім того, у ході роботи алгоритму з'являються проміжні результати, які використовуються надалі . Таким чином, кожний алгоритм має справа з даними - вхідними, проміжними й вихідними. Оскільки ми збираємося уточнювати поняття алгоритму, потрібно уточнити й поняття даних, тобто вказати, яким вимогам повинні задовольняти об'єкти, щоб алгоритми могли з ними працювати.

Зрозуміло, що ці об'єкти повинні бути чітко визначені й відрізнимими як друг від друга, так і від "необ'єктів". У багатьох важливих випадках добре зрозуміло, що це значить: до таких алгоритмічних об'єктів відносяться числа, вектори, матриці сміжностей графів, формули. Зображення (наприклад, малюнок графа) представляються менш природніми в якості алгоритмічних об'єктів. Якщо говорити про граф, то справа навіть не в тому, що в малюнку більше несуттєвих деталей і дві людини той самий граф зобразять по-різному (зрештою , різні матриці суміжності теж можуть задавати той самий граф з точністю до ізоморфізму), а в тому, що матриця суміжності легко розбивається на елементи, причому з елементів усього двох видів (нулів і одиниць) складаються матриці будь-яких графів, тоді як розбити на елементи малюнок набагато важче. Нарешті, з такими об'єктами, як "гарна книга" або "осмислене твердження", з якими легко управляється будь-яка людина (але кожна по-своєму!), алгоритм працювати відмовиться, поки вони не будуть описані як дані за допомогою інших, більш підходящих об'єктів.

Замість того щоб намагатися дати загальне словесне визначення чіткої визначеності об'єкта, у теорії алгоритмів фіксують конкретні кінцеві набори вихідних об'єктів (називаних елементарними) і кінцевий набір засобів побудови інших об'єктів з елементарних. Набір елементарних об'єктів утворює кінцевий алфавіт вихідних символів (цифр, букв і т.д. ), з яких будуються інші об'єкти; типовим засобом побудови є індуктивні визначення, що вказують, як будувати нові об'єкти із уже побудованих. Найпростіше індуктивне визначення - це визначення деякої множини слів, класичним прикладом якого служить визначення ідентифікатора в АЛГОЛі; ідентифікатор- це або буква, або ідентифікатор, до якого приписана праворуч буква або цифра. Слова кінцевої довжини в кінцевих алфавітах (зокрема , числа) - найбільш звичайний тип алгоритмічних даних, а число символів у слові (довжина слова) - природна одиниця виміру обсягу оброблюваної інформації. Більш складний випадок алгоритмічних об'єктів - формули. Вони також визначаються індуктивно й також є словами в кінцевому алфавіті, однак не кожне слово в цьому алфавіті є формулою. У цьому випадку звичайно основним алгоритмам передують допоміжні, які перевіряють, чи задовольняють вихідні дані потрібним вимогам. Така перевірка називається синтаксичним аналізом.

2. Дані для свого розміщення вимагають пам'яті. Пам'ять звичайно вважається однорідною й дискретною, тобто складається з однакових комірок, причому кожна комірка може містити один символ алфавіту даних. Таким чином, одиниці виміру обсягу даних і пам'яті погоджені. При цьому пам'ять може бути нескінченною. Питання про те, потрібна чи одна пам'ять або декілька й, зокрема , чи потрібна окрема пам'ять для кожного із трьох видів даних (вхідних, вихідних і проміжних), вирішується по різному.

3. Алгоритм складається з окремих елементарних кроків, або дій, причому множина різних кроків, з яких складений алгоритм, скінченна. Типовий приклад множини елементарних дій - система команд ЕОМ. Звичайно елементарний крок має справу з фіксованим числом символів (це зручно, наприклад, для виміру часу роботи алгоритму числом виконаних кроків), однак ця вимога не завжди виконується. Наприклад, в ЕОМ третього покоління є команди типу " пам'ять-пам'ять", що працюють із полями пам'яті змінної довжини.

4. Послідовність кроків алгоритму детермінована, тобто після кожного кроку або вказується, який крок робити далі, або дається команда зупинки, після чого робота алгоритму вважається закінченою.

5. Природно від алгоритму зажадати результативності, тобто зупинки після кінцевого числа кроків (залежного від даних) із вказівкою того, що вважати результатом. ЗОКРЕМА , всякий, хто пред'являє алгоритм розв'язку деякого завдання, наприклад обчислення функції f(x), зобов'язано показати, що алгоритм зупиняється після кінцевого числа кроків (як кажуть, сходиться) для будь-якого х з області завдання f. Однак перевірити результативність (збіжність) набагато сутужніше, чим вимоги, викладені в пп. 1-4. НА відміну від них збіжність звичайно не вдається встановити простим переглядом опису алгоритму; загального ж методу перевірки збіжності, придатного для будь-якого алгоритму А и будь-яких даних х, як буде показано далі, взагалі на загал не існує. Обговорення труднощів, пов'язаних з розпізнаванням збіжності, див. в § 5.4.

6. Слід розрізняти: а) опис алгоритму (інструкцію або програму); б) механізм реалізації алгоритму (наприклад, ЕОМ), що включає засобу пуску, зупинки, реалізації елементарних кроків, видачі результатів і забезпечення детермінованості, тобто керування ходом обчислення; в) процес реалізації алгоритму, тобто послідовність кроків, яка буде породжена при застосуванні алгоритму до конкретних даних. Будемо припускати, що опис алгоритму й механізм його реалізації кінцеві (пам'ять, як уже говорилося, може бути нескінченною, але вона не включається в механізм). Вимоги до кінцівки процесу реалізації збігаються з вимогами результативності (див. п. 5).

Приклад 5.1. Розглянемо наступну задачу: дана послідовність Р з п позитивних чисел (n — скінченне, але довільне число); потрібно впорядкувати їх, тобто побудувати послідовність R, у якій ці ж числа розташовані в порядку зростання. Майже відразу ж спадає на думку наступний простий спосіб її рішення: переглядаємо Р и знаходимо в ній найменше число; викреслюємо його з Р и виписуємо його як перше число R; знову звертаємося до Р и знаходимо в ній найменше число; приписуємо його праворуч до отриманої частини R і так далі, доти, поки в Р не будуть викреслені всі числа.

Виникае природне запитанння: що значить «і так далі». Для більшої ясності перепишемо опис способу рішення в більше чіткій формі, розбивши його на кроки й указавши переходи між кроками.

Крок 1. Шукаємо в Р найменше число.

Крок 2. Знайдене число приписуємо праворуч до R (у початковий момент R порожня) і викреслюємо його з Р.

Крок 3. Якщо в Р немає чисел, то переходимо до кроку 4. У іншому випадку переходимо до кроку 1.

Крок 4. Кінець. Результатом уважати послідовність побудовану до даного моменту.

Більшість читачів визнає такий опис досить ясним (і навіть зайве формальним), щоб, користуючись їм, однозначно одержати потрібний результат. Однак це враження ясності опирається на деякі неявні припущення, до правильності яких ми звикли, але які неважко порушити. Наприклад, що значить «дана послідовність чисел»? Чи є такою послідовність , ,(1,2)^π? Очевидно, так, однак у нашому описі нічого не сказано, як знайти найменше число серед таких чисел. У ньому взагалі не говориться про те, як шукати найменші числа, очевидно, передбачається, що мова йде про числа, представлених у вигляді десяткових дробів, і що відомо, як їх порівнювати.

Отже, необхідно уточнити форми подання даних. При цьому не можна просто заявити, що припустимо будь-яке подання чисел. Адже для кожного подання існує свій алфавіт (який, крім цифр, може включати коми, дужки, знаки операцій і функцій і т.д.) і свій спосіб порівняння чисел (наприклад, спосіб переведення в десятковий дріб), тоді як скінченнісь алфавіту вимагає фіксувати його заздалегідь, а скінченність опису алгоритму дозволяє включити в нього лише заздалегідь фіксоване число способів порівняння. Фіксація подання чисел у вигляді десяткових дробів також не вирішує всіх проблем. Порівняння 10—20 розрядних чисел уже не може вважатися елементарною дією: відразу не можна сказати, яке із чисел більше: 90811557001,15 або 32899901467,0048. У машинних алгоритмах саме подання числа ще вимагає подальшого уточнення: потрібно, по-перше, обмежити число розрядів (цифр) у числі, тому що від цього залежить, скільки комірок пам'яті буде займати число, а по-друге, домовитися про спосіб розміщення десяткової коми в числі, тобто вибрати подання у вигляді числа з фіксованої- або плаваючої комою, оскільки способи обробки цих двох подань різні. Нарешті, кожний, хто мав справу із програмуванням, відзначить, що на кроці 1 потрібно довідатися дві речі: саме найменше число (щоб записати його в R) і його місце в Р, тобто його адреса в тій частині пам'яті, де зберігається Р (щоб викреслити його з Р), а отже потрібно мати засоби вказівки цієї адреси.

Таким чином, навіть у цьому простому прикладі нескладний аналіз показує, що опису, що виглядає цілком ясним, ще далеко до алгоритму. Ми зіткнулися тут з необхідністю уточнити майже всі основні характеристики алгоритму, які відзначалися раніше: алфавіт даних і форму їхнього подання, пам'ять і розміщення в ній елементів Р и R, елементарні кроки (оскільки крок 1 явно неелементарний). Крім того, стає ясним, що вибір механізму реалізації (скажемо, людини або ЕОМ) буде впливати й на сам характер уточнення: у людини вимоги до пам'яті, поданню даних і до елементарності кроків набагато більше слабкі й «укрупнені», окремі незначні деталі він може уточнити сам.

Мабуть, тільки дві вимоги до алгоритмів у наведеному описі виконані в достатній мірі (вони-те й створюють враження ясності). Досить очевидна збіжність алгоритму: після виконання кроків 1 й 2 або робота закінчується, або з Р викреслюється одне число; тому рівно після п виконань кроків 1 й 2 з Р будуть викреслені всі числа й алгоритм зупиниться, а R буде результатом. Крім того, не викликає сумніву детермінованість: після кожного кроку ясно, що робити далі, якщо врахувати, що тут і надалі використається загальноприйнята угода - якщо крок не містить вказівок про подальший перехід, те виконуємо крок, що іде за ним в описі. Оскільки використані в прикладі засоби забезпечення детермінованості носять досить загальний характер, зупинимося на них трохи докладніше.

Блок-схеми алгоритмів. Зв'язки між кроками можна зобразити у вигляді графа. Для приклада 5.1 граф зображений на мал. 5-1.

Ні

Початок

Крок 1

Крок 2

Крок 3

Кінець

Так

Мал. 5-1.

Такий граф, у якому вершинам відповідають кроки, а ребрам - переходи між кроками, називається блок-схемою алгоритму. Його вершини можуть бути двох видів: вершини, з яких виходить одне ребро (їх називають операторами), і вершини, з яких виходять два ребра (їх називають логічними умовами, або предикатами). Крім того, є єдиний оператор кінця, з якого не виходить жодного ребра, і єдиний оператор початку. Важливою особливістю блок-схеми є те, що зв'язки, які вона описує, не залежать від того, чи є кроки елементарними або являють собою самостійні алгоритми,- як говорять у програмуванні, блоки (власне кажучи крок 1 таким й є). Можливість «розблочювати» алгоритм добре відома у програмуванні й широко там використається: великий алгоритм розбивається на блоки, які можна роздати для програмування різним особам. Для даного блоку неважливо, як улаштовані інші блоки; для програмування блоку досить знати, де лежить вся вихідна інформація, яка форма її подання, що повинен робити блок і куди записати результат.

За допомогою блок-схем можна, навпаки, кілька алгоритмів, розглянутих як блоки, зв'язати в один великий алгоритм. Зокрема, якщо алгоритм А₁ обчислюючий функцію f₁(х), з'єднаний з алгоритмом A₂, що обчислює функцію f2 (x) (мал. 5.2), і при цьому вихіднимиданими для A₂ служить результат А₁, те отримана блок-схема задає алгоритм, що обчислює f₂(f₁(x)), тобто композицію f₁ й f₂ (див. § 1.2). Таке з'єднання алгоритмів називається композицією алгоритмів.

Початок

А₁

А₂

Кінець

Мал. 5-2.

На блок-схемі добре видна різниця між описом алгоритму й процесом його реалізації. Опис - це граф; процес реалізації - це шлях у графі. Різні шляхи в тому самому графі виникають при різних даних, які створюють різні логічні умови в точках розгалуження. Відсутність збіжності означає, що в процесі обчислення не з'являється умов, що ведуть до кінця, і процес іде по нескінченному шляху (зациклюеться).

При всій наочності мови блок-схем не треба, однак, переоцінювати його можливості. Він досить грубий і відображає зв'язку лише по керуванню (що робити в наступний момент, тобто якому блоку передати керування), а не за інформацією (де цьому блоку брати вхідні дані). Наприклад, мал. 5.2 при зробленому застереженні відносно даних зображує обчислення f₂(f₁(x)), однак він же міг зображувати послідовне обчислення двох незалежних функцій f1(5) і f₂(100), порядок яких несуттєвий. Блок-схеми не містять відомостей ні про дані, ні про пам'яті, ні про використовуваний набір елементарних кроків. Зокрема, треба мати на увазі, що якщо в блок-схемі немає циклів, це ще не означае, що немає циклів в алгоритмі (вони можуть бути в якому-небудь неелементарному блоці). Власне кажучи блок-схеми — це не мова, а засіб, щоправда, дуже зручний, для однієї мети — опису детермінізму алгоритму. Воно буде неодноразово використатися надалі з однією видозміною:8 умови, тобто точки розгалуження, можуть бути не тільки двійковими, але й багатозначними; важливо лише, щоб вірною була рівно одина з можливих відповідей. Приклади таких умов: а) x<0, х=0, х>0; б) х<5, 5^x<20, х=20, х<20.

О підходах до уточнення поняття «алгоритм». Раніше були сформульовані основні вимоги до алгоритмів. Однак поняття, використані в цих формулюваннях (такі, як ясність, чіткість, елементарність), самі мають потребу в уточненні. Очевидно, що їхні словесні визначення будуть містити нові поняття, які знову зажадають уточнення, і т.д. Тому в теорії алгоритмів приймається інший підхід: вибирається скінченний набір вихідних об'єктів, які оголошуються елементарними, і скінченний набір способів побудови з них нових об'єктів. Цей підхід був уже використаний під час обговорення питання про дані: уточненням поняття «дані» надалі будемо вважати множини слів у скінченний алфавітах. Для уточнення детермінізму будуть використатися або блок-схеми й еквівалентні їм словесні описи (типу того, котрий наведений у прикладі 5.1), або опис механізму реалізації алгоритму. Крім того, потрібно зафіксувати набір елементарних кроків і домовитися про організації пам'яті. Після того як це буде зроблено, вийде конкретна алгоритмічна модель.

Алгоритмічні моделі, розглянуті в цій главі, претендують на право вважатися формалізацією поняття «алгоритм». Це значить, що вони повинні бути універсальними, тобто допускати опис будь-яких алгоритмів. Тому може виникнути природне заперечення проти пропонованого підходу: чи не приведе вибір конкретних засобів до втрати спільності формалізації? Якщо мати на увазі основні цілі, що стояли при створенні теорії алгоритмів,— універсальність і пов'язану з нею можливість говорити в рамках якої-небудь моделі про властивості алгоритмів взагалі, то це заперечення знімається в такий спосіб. По-перше, доводиться зведення одних моделей до іншим, тобто показується, що всякий алгоритм, описаний засобом однієї моделі, може бути описаний засобами іншої. По-друге, завдяки взаємному зведенню моделей у теорії алгоритмів вдалося виробити інваріантну стосовно моделей систему понять, що дозволяє говорити про властивості алгоритмів незалежно від того, яка формалізація алгоритму обрана. Ця система понять заснована на понятті обчислюваності функції, тобто функції, для обчислення якої існує алгоритм. Загальне поняття обчислюваності і його властивості будуть більш докладно розглянуті в § 5.4.

Тим не менш, хоча спільність формалізації в конкретній моделі не губиться, різний вибір вихідних засобів приводить до моделей різного виду. Можна виділити три основних типи універсальних алгоритмічних моделей, що розрізняються вихідними евристичними міркуваннями щодо того, що таке алгоритм. Перший тип зв'язує поняття алгоритму з найбільш традиційними поняттями математики — обчисленнями й числовими функціями. Найбільш розвинена й вивчена модель цього типу — рекурсивні функції — є історично першою формалізацією поняття алгоритму. Другий тип заснований на представленні про алгоритм як про деякий детермінований пристрій, здатний виконувати в кожний окремий момент лише досить примітивні операції. Таке подання не залишає сумнівів в однозначності алгоритму й елементарності його кроків. Крім того, евристика цих моделей близька до ЕОМ й, отже, до інженерної інтуїції. Основною теоретичною моделлю цього типу (створеної в 30-х раніше ЕОМ!) є машина Тьюрінга. Нарешті, третій тип алгоритмічних моделей - це перетворення слів у довільних алфавітах, у яких елементарними операціями є підстановки, тобто заміни частини слова (підслова) іншим словом. Переваги цього типу - у його максимальній абстрактності й можливості застосувати поняття алгоритму до об'єктів довільної (не обов'язково числовий) природи. Втім, як буде ясно з подальшого, моделі другого й третього типу досить близьке (їхнє взаємне зведення доводиться просто) і відрізняються в основному евристичними акцентами. Приклади моделей цього типу - канонічні системи Поста й нормальні алгоритми Маркова.

Лекція 2 Рекурсивні функції

Історично першою алгоритмічною системою була система, заснована на використанні конструктивно обумовлених арифметичних (цілочисленних) функцій, що одержали спеціальну назву рекурсивних функцій.

Рекурсією називається спосіб завдання функції, при якому значення обумовленої функції для довільних значень аргументів виражається відомим образом через значення обумовленої функції для менших значень аргументів.

Чисельні функції, значення яких можна встановити за допомогою деякого алгоритму, називаються обчислюваними функціями. Функція називається рекурсивною, якщо існує ефективна процедура для її обчислення. Поняття ефективної процедури є інтуїтивним. Говорять, що є ефективна процедура для виконання певних обчислень, якщо ці обчислення виконуються за механічними правилами, тобто по певному алгоритму.

Оскільки поняття алгоритму в цьому визначенні береться в інтуїтивному змісті, то й поняття обчислюваної функції виявляється інтуїтивним. Проте при переході від алгоритмів до обчислюваної функцій виникає одна дуже істотна обставина: сукупність процесів, що підпадають під інтуїтивне поняття алгоритму, дуже велика й мало доступна для огляду. Сукупність обчислюваних функцій для самих різних розумінь процесів виявилася однією й тією ж і притім легко описуваної у звичайних математичних термінах.

Сукупність числових функцій, що збігає із сукупністю всіх вычислимых функцій при самому широкому дотепер відомому розумінні алгоритму, зветься сукупністю рекурсивних функцій.

Гёдель уперше описав клас всіх рекурсивних функцій як клас всіх числових функцій, визначних у деякій формальній системі. Виходячи із зовсім інших передумов, Черч в 1936 р. вивів той же клас числових функцій, що й Гёдель. Черчем була сформульована гіпотеза про те, що клас рекурсивних функцій тотожний із класом усюди визначених обчислюваних функцій. Ця гіпотеза відома під ім'ям тези Черча. Поняття обчислюваної функції точно не визначається, тому тезу Черча довести не можна.

Якщо деяким елементам множини X поставлені у відповідність однозначно певні елементи множини Y, то говорять, що задано часткову функцію з X в Y.

Сукупність тих елементів множини X, у яких є відповідні в Y, називається областю визначеності функції, а сукупність цих елементів множини Y — сукупністю значень функції. Якщо область визначеності функції з X в Y збігається із множиною X, то функція називається всюди певної.

Кліні ввів поняття частково рекурсивної функції й висловив гіпотезу, що всі часткові функції, обчислювані за допомогою алгоритмів, є частково рекурсивними. Ця гіпотеза також недоказова, як і гіпотеза Черча. Однак математичні дослідження останніх 30 років виявили повну доцільність уважати поняття частково рекурсивної функції науковим еквівалентом інтуїтивного поняття обчислюваної часткової функції.

Надалі під тезою Черча будемо розуміти гіпотезу Черча в тому розширеному виді, що був доданий їй Кліні.

Теза Черча виявився достатньою, щоб додати необхідну точність формулюванню алгоритмічних проблем й у ряді випадків уможливити доказ їхньої нерозв'язності. У силу тези Черча питання про обчислюваність функції рівносильне питанню про її рекурсивність. Поняття рекурсивної функції суворе. Тому звичайна математична техніка дозволяє іноді безпосередньо довести, що вирішуюча задачу функція не може бути рекурсивною, тобто задача нерозв'язна.

Застосування рекурсивних функцій у теорії алгоритмів засновано на ідеї нумерації слів у довільному алфавіті послідовними натуральними числами. Найбільш просто таку нумерацію можна здійснити, розташовуючи слова в порядку зростання їхніх довжин, а слова, що мають однакову довжину, - у довільному (лексикографічному) порядку.

Після нумерації вхідних і вихідних слів у довільному алфавітному операторі цей оператор перетворюється у функцію y = f(x), у якій аргумент х і функція y приймають ненегативні цілочисленні значення. Функція f(x) може бути визначена не для всіх значень х, а лише для тих, які становлять область визначення цієї функції.

Подібні частково певні цілочисленні й цілозначні функції для стислості називаються арифметичними функціями, серед них виділимо найбільш прості й будемо їх називати елементарними арифметичними функціями:

1) функції, тотожно рівні нулю:

Oⁿ(x₁, x₂, ... , x_n) = 0,

певні для всіх ненегативних значень аргументів;

2) тотожні функції, що повторюють значення своїх аргументів:

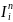(x₁, x₂, . . ., Xn) = Xi (1≤i≤n; n = 1, 2, ...), окремий випадок (х) = х;

3) функції безпосереднього проходження:

S¹(x)=x+1

також певні для всіх цілих ненегативних значень свого аргументу.

Використовуючи в якості вихідних функції перераховані елементарні арифметичні функції, можна за допомогою невеликого числа загальних конструктивних прийомів будувати усе більше й більше складні арифметичні функції. У теорії рекурсивних функцій особливо важливе значення мають три операції: суперпозиції, примітивної рекурсії й найменшого кореня. Розглянемо кожну з них.

Операція суперпозиції функцій полягає в підстановці одних арифметичних функцій замість аргументів інших арифметичних функцій.

Нехай задані п функцій f₁, ..., f_п від m змінних кожна й функція f(x_1, ..., х_п) від п змінних. Операція суперпозиції функцій f₁, ..., f_n з f дасть нам функцію

g(x₁, …, x_m)=f(f₁(x₁, … ,x_m), … ,f_n(x₁, … ,x_m))...

Наприклад, здійснюючи операцію суперпозиції функцій f(x) = 0 й g(x) = х + 1, одержимо функцію

h(x)=g(f(x))=0+1=1.

При суперпозиції функції g(x)c самою собою одержимо функцію h(x) = x + 2 і т.п.

Операція суперпозиції позначається символом Sⁿ⁺¹, де індекс зверху означає число функцій.

Операція примітивної рекурсії дозволяє будувати п + 1-місну арифметичну функцію (функцію від п + 1 аргументу) по двох заданих функціях, одна йз яких є n-місною, а інша п + 2-місною.

Нехай задані які-небудь числові часткові функції: п-містна g і п + 2-містна h. Говорять, що п + 1-містнаа часткова функція f виникає з функцій g й h примітивною рекурсією, якщо для всіх натуральних значень х₁ ,..., х_п, у маємо:

f(x₁, …, x_n, 0)=g(x₁, …, x_n); (3)

f(x₁, ..... , х_п, в+1)=h(x₁, ... , х_п, в, f( x₁, ... , х_п, у)). (4)

Для правильного розуміння операції примітивної рекурсії необхідно помітити, що всяку функцію від меншого числа змінних можна розглядати як функцію від будь-якого більшого числа змінних. Зокрема, функції-константи, які природно розглядати як функції від нуля аргументів, можна розглядати як функції від будь-якого кінцевого числа аргументів.

Відповідно до цього операцію примітивної рекурсії будемо застосовувати й для п = 0, говорячи, що одномісна часткова функція f виникає примітивною рекурсією з постійної одномісної функції, рівної числу а, і двумістної часткової функції h, якщо

f(0) =а;

f(x+1)=h(x, f(x)).

Встає питання, для чи кожних g й h існує функція f і чи буде вона єдиною. Область визначення функції -множина всіх натуральних чисел, тому відповідь на обидва питання позитивний.

Якщо f існує, то з (3) і (4) знаходимо:

f(x₁, ...,x_n, 0) =g(x₁, ... , х_п); (5)

f(x₁, …, x_n, 1)=h(x₁, …, x_n, 0, g(x₁, ..... , х_п));

f(x₁, …, x_n, 2)=h(x₁, …, x_n, 1, f(x₁, ..... , х_п, 1));

. . . . . . . . .

f(x₁, …, x_n, m+1)=h (x₁, …, x_n, m, f(x₁, ..... , х_n, т))

і тому f визначена однозначно. Таким чином, для будь-яких часткових n-містної функції g і п + 2-містної функції h/n = 0, 1, 2, ... існує тільки одна часткова п + 1-містна функція f, що виникає з g й h примітивною рекурсією. Символічно пишуть f = R(g, h).

З (5) видно, що якщо ми якимось чином уміємо знаходити значення g й h, то значення f можна обчислити за допомогою процедури цілком механічного характеру. Для знаходження значення f(a₁ ..., а_п, т + 1) досить послідовно знайти числа:

b₀=g(a₁, …, a_n);

b₁=h(a₁, …, a_n, 0, b₀);

b₂=h(a₁, …, a_n, 1, b₁);

....... . . . . . . . .

b_m+1 = h(a₁, ... , a_n, m, b_m).

Отримане на m + 1 кроці число b_m+1 і буде шуканим значенням f у крапці (a₁, …, a_n, m+1)...

Як приклад застосування операції примітивної рекурсії покажемо, як за допомогою цієї операції з елементарних функцій можна побудувати двумістну функцію підсумовування f(x, у) = х + y.

Ця функція визначається за допомогою тотожної функції g(x) = х і функції безпосереднього проходження:

h(x, в, z) = z + 1.

Справді, використовуючи правила (3) і (4), маємо:

f(x,0) =g(x) =х;

f(x, 1) =h(x,0, х) =x+1;

f(x, 2)=h(x, 1, х+1)=х + 2;

. . . . . . . .

f(x, у— 1) =h(x, в — 2, х + в — 2) = х + в-1;

f(x, y) = h(x, у-1, x + y-1)=x + y.

Аналогічно можна побудувати показову, степенну й іншої відомої арифметичної функції.

Функції, які можуть бути побудовані з елементарних арифметичних функцій за допомогою операцій суперпозиції й примітивної рекурсії, застосованих будь-яке кінцеве число раз у довільній послідовності, називаються примітивно рекурсивними функціями.

Операції суперпозиції й примітивної рекурсії, будучи застосовані до всюди певних функцій, дають у результаті знову всюди певні функції.

Як приклад доведемо примітивну рекурсивність деяких простих арифметичних функцій.

Двуміста функція f(x, у) = х + у задовольняє співвідношенням:

х + 0 = х = (х) -тотожна функція;

х + (в + 1) = (х + у) + 1 = S(x + у) — функція безпосереднього проходження.

Отже, функція х + у виникає із примітивно рекурсивних функцій і h(x, в, z) = z + I операцією примітивної рекурсії й тому функція х + в — примітивно рекурсивна.

Двуміста функція f(x, у) = х. у задовольняє схемі примітивної рекурсії:

х. 0 = 0(х);

х(y+1) = ху + х,

с початковими примітивно рекурсивними функціями

g(x) =0(х), h(x, в, z)=z + x,

тому функція х. у примітивно рекурсивна.

В області натуральних чисел різницю х — у природно вважати часткової двумістною функцією від х и y, певної лише для х≥y, тому що від'ємні числа не входять у розглянуту область. Але примітивно рекурсивні функції всюди певні. Тому в теорії примітивно рекурсивних функцій замість звичайної різниці вводять усічену різницю, позначувану символом 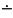і обумовлену в такий спосіб:

(*)

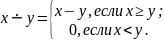На відміну від простої різниці усічена різниця в області натуральних чисел усюди визначена, і в той же час вона дуже просто пов'язана зі звичайною різницею. Так, наприклад, відповідно до визначення (*):

5 3 = 2; 3 5=0, (х у) z = х (в + z).

Функція х 1 задовольняє примітивно рекурсивній схемі

0 1 = 0;

(x + 1) 1 = х,

с примітивно рекурсивними початковими функціями ПРО¹ й 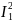. Тому функція x 1 - примітивно рекурсивна.

З іншого боку, з (*) треба, що для будь-яких х, в

x 0= х;

х (в+1) =(х у) 1.

Ці тотожності показують, що двуместная функція x y виникає примітивною рекурсією з функції і h(x, y, z) = z 1. Обидві останні функції примітивно рекурсивні, тому й функція х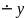 — примітивно рекурсивна.

Більшість арифметичних функцій відносяться до примітивно рекурсивних. Проте примітивно рекурсивні функції не охоплюють всіх арифметичних функцій, які можуть бути визначені конструктивно. При побудові всіх цих функцій використаються інші операції, зокрема операція найменшого кореня.

Операція найменшого кореня, або операція мінімізації, дозволяє визначити нову арифметичну функцію f(x₁,…, х_п) від п змінних за допомогою раніше побудованої арифметичної функції g(x₁ ..., х_п, у) від п + 1 змінних.

Для будь-якого заданого набору значень змінних x₁ = a₁,..., x_n = а_п як відповідне значення f(a₁, .. ., а_п) обумовленої функції f(x₁, …, х_п) приймається найменший цілий ненегативний корінь y= а рівняння g(a₁ , ..., а_п, у) = 0,

В випадку неіснування цілих ненегативних корінів у цього рівняння функція f(x₁, ..., х_п) уважається невизначеною при відповідному наборі значень змінних.

Арифметичні функції, які можуть бути побудовані з елементарних арифметичних функцій за допомогою операцій суперпозиції, примітивної рекурсії й найменшого кореня, називаються частково рекурсивними функціями. Якщо такі функції виявляються до того ж усюди визначеними, то вони називаються загальрекурсивними функціями.

У цьому визначенні, як й у визначенні примітивно рекурсивних функцій, передбачається можливість виконання всіх припустимих операцій у будь-якій послідовності й будь-яке кінцеве число раз.

Частково рекурсивні функції являють собою найбільш загальний клас конструктивно обумовлених арифметичних функцій.

Поняття частково рекурсивної функції - одне з головних понять теорії алгоритмів. Значення його полягає в наступному.

1. Кожна стандартно задана частково рекурсивна функція обчислювана шляхом певної процедури механічного характеру.

2. Які би класи точно обкреслених алгоритмів дотепер фактично не будувалися, у всіх випадках незмінно виявлялося, що числові функції, обчислювані за допомогою алгоритмів цих класів, були частково рекурсивними. Тому загальноприйнятою є наступна наукова гіпотеза, відома під ім'ям тези Черча.

Клас алгоритмічно (або машинно) обчислюваних часткових: числових функцій збігається із класом всіх частково рекурсивних, функцій. Ця теза дає алгоритмічне тлумачення поняттю частково рекурсивних функцій.

Практично поняттям частково рекурсивних функцій користуються для доказу алгоритмічної можливості розв'язання або нерозв'язності проблем.

Використання ж частково рекурсивних функцій для подання того або іншого конкретного алгоритму практично недоцільно через складність такого процесу алгоритмізації.

Вправи:

1. Побудувати функції додавання й розписати алгоритм у вигляді послідовних кроків з використанням рекурсивних функцій:

а) тримісну функцію додавання;

б) n-містну функцію додавання.

2. Побудувати функції множення й розписати алгоритм у вигляді послідовних кроків з використанням рекурсивних функцій:

а) двомісну функцію множення;

б) тримісну функцію множення;

в) n-містну функцію множення.

3. Побудувати функції піднесення в ступінь і розписати алгоритм у вигляді послідовності кроків для:

а) двомісної функції;

б) тримісної функції;

в) n-містної функції:

4. Побудувати часткову двомісну функцію ділення й розписати алгоритм у вигляді послідовності кроків.