Лекція 7 Формальні перетворення алгоритмів

Одним з основних питань, що виникають у процесі перетворення алгоритмів, є їхня еквівалентність. Нагадаємо, що два алгоритми вважаються еквівалентними, якщо вони мають ту саму область визначення, реалізовані ними функції збігаються, а система правил різна.

Можна визначити сильну й слабку еквівалентність алгоритмів. Два алгоритми будемо називати слабко еквівалентними, якщо вони мають ту саму область визначення й результати переробки однакових слів із цієї області збігаються.

Два алгоритми будемо називати сильно еквівалентними, якщо вони мають однакову область визначення й збігаються не тільки результати переробки слів із цієї області, але й сам процес їхньої переробки.

В «чистому виді» поняття еквівалентності двох алгоритмів U₁ й U₂ будемо визначати в такий спосіб. Для кожного алгоритму вводиться поняття «входу» й «виходу». Для кожного входу, що має сенс для даного алгоритму, виконання алгоритму може приводити до деякого виходу. Нехай x₁ й x₂ — входи алгоритмів U₁ й U₂ відповідно. Алгоритми U₁ й U₂ уважаються еквівалентними, якщо з умови x₁ = x₂ слідуе, що якщо хоча б один алгоритм, наприклад U₁, має вихід y₁ то й інший алгоритм також має вихід y₂, причому y₁=y₂.

Таким чином, еквівалентність «у чистому виді» має місце тоді, коли рівність входів приводить до рівності виходів. На практиці велике значення має більше загальний спосіб введення еквівалентності, а саме визначення еквівалентності з точністю до ізоморфізму. У цьому випадку для з'ясування питання про еквівалентності зіставляються один з одним не рівні входи й виходи, а лише що перебувають у відповідності, що задається ізоморфізмом.

У цьому випадку між деякими входами x₁ алгоритму U₁ і входами x₂ алгоритми U₂ конструктивно задається деякий ізоморфізм I (у цьому випадку просто як однозначну відповідність,). Аналогічно задається деякий ізоморфізм J між виходами y₁ й y₂ алгоритмів U₁ й U₂ відповідно.

Предикат від двох конструктивних об'єктів А и В «бути у відповідності, заданому ізоморфізмом L» будемо позначати через А_L~В.

Еквівалентність тепер буде визначатися в такий спосіб. Алгоритми U₁ й U₂ уважаються еквівалентними, якщо з умови х₁~х₂ випливае, що якщо хоча б один алгоритм має вихід y₁, то й інший алгоритм також має вихід y₂, причому y₁~y₂.

Різні види еквівалентності відрізняються тим, як визначаються «входи» й «виходи» алгоритму, а також тим, як фактично вибираються изоморфізми I й J.

Між різними видами еквівалентності можна ввести часткове відношення порядку, що виражається словами «сильніше» й «слабше». Будемо вважати, що відношення еквівалентності Э1 слабше відношення еквівалентності Э₂, якщо будь-які алгоритми U₁ й U₂, еквівалентні в змісті Э₂, еквівалентні й у змісті Э₁, і в той же час є хоча б одна пара алгоритмів ₁ і ₂, таких, що ₁ і ₂ які еквівалентні в змісті Э1 і не еквівалентні в змісті Э₂.

Очевидно, чим слабше відношення еквівалентності, тим ширше класи алгоритмів, еквівалентних відповідно до цього відношення. Природним є прагнення розширити класи еквівалентних алгоритмів, уводячи більш слабке визначення еквівалентності. Однак при занадто слабкому визначенні еквівалентності масові проблеми, що виникають у теорії алгоритмів, і серед них основна проблема розпізнавання еквівалентності алгоритмів, можуть виявитися нерозв'язними. З іншого боку, занадто сильне визначення еквівалентності надмірно звужує класи еквівалентних алгоритмів. Правильний вибір поняття еквівалентності відіграє більшу роль як з погляду можливості одержання змістовних теорем, так і з погляду їхньої практичної застосовності.

На ступінь широти поняття еквівалентності найбільше істотно впливає вибір визначення «виходу» алгоритму. Не у всіх випадках нас можуть цікавити як вихід тільки ті конструктивні об'єкти, які формально оголошуються результатами по закінченні виконання алгоритму. У деяких випадках для нас є важливою інформація про які-небудь проміжні результати або про те, у якій послідовності виконувалися елементарні акти алгоритму й т.д. Тому в самому загальному змісті під виходом алгоритму варто розуміти якийсь запис всієї тієї інформації, яку можна одержати, спостерігаючи процес виконання алгоритму.

Таким чином, чим більше інформації, отриманої в ході виконання алгоритму, несе в собі вихід, тим більш сильним виявляється відношення еквівалентності, засноване на такому визначенні виходу. Інакше кажучи, вся розмаїтість еквівалентних алгоритмів полягає в тому, що той самий скінченний результат виходить різними шляхами. Отже, чим більше історії про те, як виконувався алгоритм, містить у собі вихід, тим до більше сильного поняття еквівалентності він приводить. Це пояснюється тим, що в один клас еквівалентних алгоритмів попадають тільки ті з них, історія виконання яких відповідає історії, зафіксованої в даному виході.

Вичерпну інформацію про те, як відбувалося виконання алгоритму, можна одержати, розглядаючи як вихід алгоритму всю послідовність виконуваних операторів-значення операторного алгоритму. У цьому випадку алгоритми вважаються еквівалентними, якщо їх значення збігаються при однакових входах. Таке визначення еквівалентності розглядалося Ю. И. Яновым, для операторних алгоритмів Ляпунова. У цьому випадку їм була доведена можливість розв'язання проблеми еквівалентності. Однак таке визначення еквівалентності є занадто сильним і багато алгоритмів, які розумно вважати еквівалентними, при такому визначенні виявляються нееквівалентними.

Виходячи із цього як вихід операторного алгоритму доцільно розглядати щось таке, що по кількості інформації про хід виконання алгоритму було б чимсь середнім між значенням алгоритму й значенням результативного змінного по закінчені виконання алгоритму. Із ціеї точки зору будемо розглядати як вихід S-подання тих змінних, значення яких нас цікавлять як результати виконання операторного алгоритму.

Якщо ввести визначення еквівалентності, що базується на використанні S-подання як вихід, то тоді можна сказати, що два алгоритми еквівалентні стосовно виділеним змінного в тому випадку, якщо відповідні змінні при співпадаючих входах обчислюються по однакових формулах. S-подання змінного є не що інше, як явне вираження формули, по якій обчислювалося результуюче значення змінного для даних вихідних значень функціональних змінних.

Як відомо, у програмуванні важливу роль грають саме такі перетворення алгоритмів, які залишають розрахункові формули (S-подання) незмінними. Дійсно, такі основні прийоми програмування, як розбивка задачі на частини, розчленовування формул, виділення проміжних результатів, перетворення логічних операторів, економія команд і комірок пам'яті, приводять до таких перетворень алгоритмів, які зберігають S-подання результативних змінних.

Для визначення еквівалентності операторних алгоритмів розглянемо два алгоритми —U₁ й U₂ з деякого класу операторних алгоритмів. Для кожного з алгоритмів виділимо ті змінні, які нас цікавлять як результати виконання цих алгоритмів. Виділені змінні можуть бути різними, в алгоритму U₁ й алгоритму U₂, .але число їх повинне бути однаковим і між ними повинне бути встановлене взаємно однозначна відповідність. Те ж саме стосується функціональних змінним алгоритмів U₁, U₂ і до параметрів цих алгоритмів, які можуть входити в S-подання виділених змінних. Позначимо функціональні змінні, параметри й виділені змінні алгоритму U₁, буквами х₁, ..., x, р₁, ..., р_r й y₁, ..., у_п відповідно. Відповідні ним змінні, граючі аналогічну роль для U₂, позначимо буквами ₁, ..., _S; ₁ , . . . , _r І ₁, . . . , _п.

Алгоритми U₁ й U₂ еквівалентні стосовно виділеним змінних, y₁, . . . , у_п й ₁, . . . , _п, якщо для будь-якого набору вихідних даних х₁, ..., хS має місце наступне твердження: якщо який-небудь із цих алгоритмів, наприклад U₁має значення для вихідних даних х₁, ..., x й S-подання виділених змінних мають вигляд:

то інший алгоритм — U₂ також має значення для вихідних даних ₁, ..., _S і S-подання виділених змінних мають вигляд:

Можна також визначити еквівалентність між двома алгоритмами U₁ й U₂ з різних класів U₁(γ₁, φ₁₎ і U₂(γ₂, φ₂₎. Відповідність між функціональними змінними, параметрами й виділеними змінними встановлюються так само, як і вище. Однак може виявитися, що списки операцій φ₁ й φ₂, а також значення функціональних змінних не збігаються буквально. У цьому випадку між операціями зі списків φ₁ й φ₂, а також між можливими значеннями функціональних змінних із множин γ₁ й γ₂ необхідно додатково задати певні ізоморфізми й уважати алгоритми U₁ й U₂ еквівалентними в тому випадку, якщо ізоморфні набори вихідних даних приводять до S-подань, що збігають із точністю до ізоморфізму утворюючих їх операцій.

Прикладом ізоморфізму операцій можуть служити наступні подання арифметичних операцій:

( ) + ( ) і ( )+( );

( ) - ( ) і ( )-( );

( ) ( ) і ( ) ( );

( ) / ( ) і ()/();

Слід зазначити, що якщо вводиться поняття еквівалентності для алгоритмів з різних класів, то може виявитися, що алгоритми, еквівалентні в змісті S-подань, будуть нееквівалентні в змісті збігу значень виділених змінних. Це може відбутися в тому випадку, якщо ізоморфні операції не будуть збігатися функціонально. Наприклад, в одному випадку арифметичні дії виконуються у двійковій системі, а в іншому - у десятковій.

Виявляється, що проблеми еквівалентності й розпізнавання приналежності алгоритму до деякого класу алгоритмів у своїй повній постановці алгоритмічно нерозв'язні. Тому дотепер їх вирішували тільки для деяких видів алгоритмічних систем при досить вузькому визначенні еквівалентності. Основні результати, отримані в цій області, належать до операторних систем алгоритмізації, зокрема до операторним схем А. А. Ляпунова, називаним часто схемами програм. Характерні риси операторних схем полягають у наступному:

сукупність операторів, що утворять схему алгоритму, зображується в схемі явно;

для кожного оператора явно вказуються його приймачі й попередники по виконанню і його аргументи й результати (входи й виходи оператора);

при побудові реалізації приймач оператора звичайно вибирається довільно, без обліку історії руху до даного оператора;

якщо в розгляд утягується деяка величина, «вироблювана» деяким оператором, то вона трактується як незалежна змінна, тобто вважається, що після виконання даного оператора вона може приймати будь-яке значення незалежно від попередньої історії;

якщо аргументом або результатом оператора виявляється деякий компонент масиву, що вказується індексом, то конкретне значення індексу звичайно ігнорується й уважається, що аргументом або результатом оператора є весь масив.

Важливе місце в процесі перетворення алгоритмів займають різні міри якості. Звичайно вони носять характер числових функціоналів, але в загальному випадку ними можуть бути будь-які об'єкти, що допускають відношення порядку.

Міри якості визначаються конкретними умовами постановки задачі, але вони завжди пов'язані з «просторово-тимчасовими» характеристиками алгоритму, тобто з часом його виконання й об'ємом пам'яті, необхідним для зберігання переробляємої информации.

Першою роботою, присвяченою загальної теорії перетворення алгоритмів, з'явилася робота Ю. И. Янова «Про логічні схеми алгоритмів». У ній були сформульовані основні компоненти теорії перетворення алгоритмів. До цих компонентів належать: формалізація поняття схеми алгоритму, завдання відношення еквівалентності, знаходження алгоритму, що розпізнає еквівалентність схем, побудова системи перетворень, повної в тому розумінні, що будь-яку пару еквівалентних алгоритмів можна трансформувати один в іншій послідовним застосуванням цих перетворень, що зберігають еквівалентність.

Усякий алгоритм при переробці конкретного об'єкта пропонує однозначно певну послідовність елементарних дій. Така послідовність, загалом кажучи, різна для різних об'єктів, до яких даний алгоритм може бути застосований. Однак завжди найдеться скінченна множина предикатів, що характеризують деякі властивості об'єктів, що переробляються, така, що для даного алгоритму залежність порядку виконання елементарних операцій від перероблюваних об'єктів, буде однозначною функцією цих предикатів. Така функція може бути записана за допомогою скінченного рядка, складеного із символів елементарних дій А₁, A₂,..., А_п (називаних операторами), предикатів і деяких допоміжних символів:

називаних відповідно лівою й правою напівдужками. При цьому рядок

A_i1A_i2 ... A_is

означає, що повинні бути виконані послідовно оператори

A_i1, A_i2, ... A_is

Рядок

де а — деякий предикат, означає, що після виконання оператора А_i1 у випадку, якщо α = 1, повинен бути виконаний оператор A_i2, що стоїть безпосередньо правіше , а якщо α = 0, то оператор А_із, що стоїть праворуч від напівдужки .

Рядки такого виду будемо називати схемними записами алгоритмів. Розглянемо приклад схемного запису нормального алгоритму. Нехай схема нормального алгоритму в деякому алфавіті А має вигляд:

де формула

є заключною підстановкою. Позначимо через р_i предикат: «слово P_i входить у перероблюєме слово», а через А_i — операцію заміни першого входження слова P_i у перероблюєме слове, на слово Qi(i = 1, 2,..., п). Тоді рядок

є схемний запис розглянутого нормального алгоритму. (0 означає тотожно хибний предикат).

Ясно, що для всякого слова R в алфавіті A послідовність операцій

A_i1, A_i2,... (1≤is≤n; s= 1, 2, ...)

над цим словом, що предписує схемний запис, збігається з послідовністю тих перетворень слова R, що виникає при застосуванні до нього нормального алгоритму з даною схемою.

Аналогічним чином можна говорити про схемні записи алгоритмів, що задаються програмами універсальних обчислювальних машин, які в цьому випадку називаються схемами програм.

Якщо в схемних записах алгоритмів відволіктися від змістовного змісту операторів, уважаючи їх елементарними символами, а предикати відповідно незалежними логічними змінними, то отримані вираження ми будемо називати логічними схемами алгоритмів.

Неважко переконатися, що той самий алгоритм при фіксованій множині елементарних операцій і предикатів може мати різні логічні схеми. Наприклад, вираз

є схемними записами того самого алгоритму при будь-якій підстановці конкретних операторів і предикатів відповідно замість A₁, A₂ й p₁, p₂.

Будемо вважати, що значення логічних змінних можуть змінюватися тільки в моменти виконання операторів. При цьому оскільки в логічних схемах алгоритмів не міститься ніякої інформації про поводження значень логічних змінних, то деякі обмеження на можливості їхньої зміни ми будемо задавати ззовні за допомогою так званих розподілів зсувів, тобто відповідностей між операторами й множинами логічних змінних.

Якщо задано який-небудь розподіл зсувів A_i — Р_i, де A_i— операторів, а Р_i — множини логічних змінних (i = 1, 2, ...), то будемо вважати, що в момент виконання оператора A_i можуть змінюватися значення тільки тих логічних змінних, які входять в P_i.

Нехай є деяка схема. Задамо для неї послідовність Δ_s1, Δ_s2,..., Δ_sm ,... наборів значень логічних змінних. Якщо вважати, що при виконанні схеми вони змінюються відповідно до цієї послідовності, тобто після виконання т-го оператора логічні змінні приймають набір значень Аз_т+1, то одержимо певну послідовність виконаних операторів, що будемо називати значенням схеми для даної послідовності наборів. Завдання розподілу зсувів виділяє для кожної схеми із всіх можливих послідовностей наборів множину припустимих послідовностей. Таким чином, припустимі послідовності відрізняються значеннями тільки тих змінних, які даним розподілом зсувів поставлені у відповідність операторові, виконаному при попередньому наборі.

Поняття рівносильності схем, при заданому розподілі зсувів вимагає збігу значень рівносильних схем для будь-якої припустимої послідовності наборів. Це означає, що множина всіх рівносильних схем при будь-якій підстановці конкретних операторів і предикатів (зв'язок яких відповідає даному розподілу зсувів) переходить у множину схемних записів одного й того самого алгоритму.

Ю. И. Яновим уводиться система аксіом і правил виводу, що описує поняття рівносильності логічних схем алгоритмів при даному розподілі зсувів. А. П. Єршовим теорія логічних схем алгоритмів Янова була перенесена на мову графі-схем, що дозволило спростити аксіоматику перетворень. Замість 14 аксіом Янова Єршов використовує тільки 7 аксіом. Н. А. Крініцкій розширив систему перетворень Янова, уводячи в розгляд інформаційні зв'язки між операторами. Оператор розглядається як система функцій, що беруть свої аргументи з деяких вхідних величин і записуючих результати у вихідні величини оператора.

Подальше розширення системи перетворень Янова йшло в напрямку перетворення не алгоритмів, а програм. Перетворення програм розглядається в роботах Н. А. Крініцкого, Р. И. Подловченко й ін.

Оскільки перетворення алгоритмів у викладі Янова є досить важким, то ми розглянемо спрощену систему перетворень, запропоновану Єршовим.

Операторною схемою Янова називається скінченний орієнтований граф, що має наступні властивості. Вершини графа мають не більше двох вихідних на них стрілок. Вершини, з яких виходять по дві стрілки (одна зі стрілок деяким чином позначається), називаються розпізнавачами, інші називаються операторами. До однієї з вершин веде спеціальна вхідна стрілка.

Позначені стрілки називаються плюс-стрілками, а непомічені- мінус-стрілками. У графі є тільки одна вершина, що не має вихідної стрілки, називана кінцевим оператором.

Кожному розпізнавачу зіставляється логічна умова α -довільна функція алгебри-логіки, що залежить від k логічних змінних p₁,..., р_k. Розпізнавач R із зіставленою йому умовою а позначається R(α).

Кожному операторові А, крім кінцевого, приписується деякий набір

Р {р₁, ... , р_k} .

логічних змінних, називаний зрушенням по логічним змінним. Оператор А с приписаним йому зсувом позначається A(P).

Сукупність зсувів Р₁, ..., Р_п всіх операторів А₁, ..., А_п, операторної схеми Янова називається розподілом зсувів, приписаним схемі G.Якщо для будь-якого i(1≤i≤n)Р_i= Λ (порожня множина), то

розподіл зсувів називається порожнім; при Р_i= {р₁, ..., p_п} розподіл зсувів називається універсальним.

Всі оператори однієї операторної схеми вважаються попарно різними. Операторна схема Янова G з операторами А₁, ..., А_п, логічними змінними р₁, . .., р_k позначається G(А₁, ...А_п, р₁, р_к). Приклад зображення операторних схем Янова наведений на мал. 8. Розпізнавач із логічною умовою p Λ позначається на схемі просто p .

Визначимо поняття еквівалентності операторних схем Янова. Нехай дана схема G(А₁, ..., А_п, p₁, ..., р_k). Будемо позначати буквою Δ з індексом або без нього впорядкований двійковий набір значень змінних р₁, ... , p_k.

Для операторної схеми G визначимо поняття конфігурації, що будується за допомогою породжуючого процесу блукання за схемою G, що задає по індукції. Сама конфігурація буде виходити у вигляді подвійної послідовності наборів значень логічних змінних р₁, ..., p_k і символів операторів A₁,..., А_п, записуваних у вигляді двох рядків: верхньої для наборів і нижньої для операторів.

При побудові конфігурації ґрунтуємося на деякому базисі індукції, від якого здійснюються наступні кроки індукції. Їхня побудова наступна.

Базис індукції. У верхній рядок записується довільний набір Δ1, нижній рядок порожній. Рух за схемою G починається в напрямку, зазначеному вхідною стрілкою.

Крок індукції. Нехай відбувається рух за схемою з набором Δ. Якщо стрілка приводить до розпізнавача R(α), то обчислюється α(Δ). Якщо α(Δ) = 1, то з тим же набором рух триває по плюсі-стрілці, що виходить із розпізнавача R. Якщо α(Δ) = 0, то рух відбувається по мінус-стрілці. Якщо стрілка приведе до оператора А (Р), то виписуємо символ оператора А в нижній рядок конфігурації й перетворимо набір Δ у набір Δ' з такою умовою, щоб набір Δ' відрізнявся від Δ значеннями тільки, може бути, тих змінних з p₁, ..., р_k, які входять у зсув Р оператора А.

Набір Δ' виписується у верхній рядок конфігурації, і рух триває по стрілці, що виходить із А.

Якщо стрілка приводить до кінцевого оператора, то його символ виписується в нижній рядок і побудова конфігурації обривається:

При русі по розпізнавачах можливий випадок, коли, не потрапивши ні на один з операторів, ми прийдемо знову до недавно пройденого розпізнавача. У цьому випадку рух по розпізнавачу стане безкінченним. При виявленні такого циклу рух штучно переривається й у нижній рядок ставиться символ порожнього періоду ( ).

Таким чином, будь-яка конкретна конфігурація має вигляд:

Δ₁ Δ_2... …

A_j1 A_j2…,

при цьому вона або є нескінченної, або обривається (на нижньому рядку) символами або ( ).

Будь-яка пара сусідніх наборів Δ_m, Δ_m+1 може відрізнятися значеннями тільки тих змінних, які входять у зрушення оператора А_jт.

Верхня послідовність наборів називається припустимою послідовністю s наборів для схеми G, нижня послідовність операторів називається значенням z схеми G, обумовленим припустимою послідовністю s.

Оскільки при побудові конфігурації можливе свавілля у виборі Δ₁ при переході від Δ_m до Δ_m+1, очевидно, що правило ставить у відповідність кожній схемі G деяку множину конфігурацій К (G), що є в загальному випадку нескінченною.

К онфігурацію, у якій при її побудові символи розпізнавачів виписуються в нижньому рядку так само, як й оператори, будемо називати точною конфігурацією. Таким чином, точна конфігурація реєструє проходження всіх вершин при русі за схемою. Очевидно, що між конфігураціями й точними конфігураціями однієї схеми існує взаємно однозначна відповідність. Приклад точної конфігурації для приклада 1 має вигляд:

10_ 10 _10 10 10 10

p рq А₃ ( ) р q

Відношення еквівалентності визначається для будь-якої пари операторних схем G₁ й G₂ з тими самими логічними змінними p₁..., р_k. Схеми G₁ й G₂ є еквівалентними (G₁ G₂), якщо K(G₁) = K(G₂), тобто якщо збігаються їхньої множини конфігурацій.

Еквівалентність схем має властивості рефлексивності (G₁ G₁) і симетричності (якщо G₁ G₂, то G₂ G₁). Як указувалося, система правил перетворень операторних схем Янова побудована у вигляді логічного числення, тобто сукупності аксіом і правил виводу.

А ксіоми в цьому численні постулюют безумовну можливість заміни деякого фрагмента операторної схеми на інший фрагмент, що предписаний даною аксіомою.

Правила виводу постулюют можливість заміни одного фрагмента на іншій при виконанні деяких умов, що втримуються в посилці даного правила виводу.

Фрагментом операторної схеми G називається деяка частина (підграф) схеми G для якої зазначений її зв'язок з іншими вершинами схеми G. Цей зв'язок указується у вигляді входів і виходів фрагмента.

Входи фрагмента-це різні стрілки, що показують, до яких вершин фрагмента ведуть стрілки від інших вершин схеми. Входи фрагмента можуть бути зазначені також у вигляді узагальненого входу, що вказує, до якої вершини може вести довільна сукупність стрілок, що виходять або від інших вершин схеми, або (якщо це не забороняється спеціальним застереженням) від виходів цього ж фрагмента. Узагальнені входи вказуються жирними стрілками. Виходи фрагмента - це різні стрілки, які показують, які вершини фрагмента з'єднані з іншими вершинами схеми. Входи мітяться римськими цифрами, виходи - арабськими.

П ояснимо зроблені визначення на прикладі фрагмента, представленого на мал. 9.

Як бачимо, до верхнього розпізнавача обов'язково підходить деяка стрілка. В оператор А ззовні можуть входити будь-які стрілки. У нижній розпізнавач можуть вести ззовні будь-які стрілки, але серед них не може бути жодна з вихідних стрілок фрагмента, позначених цифрою 2. Позначка двох вихідних стрілок однієї й тією же цифрою означає, що обидві ці стрілки повинні вести до одній і тій же вершині схеми.

Самі аксіоми й твердження правил виводу мають вигляд співвідношень рівносильності, тобто двох фрагментів, розділених знаками рівносильності ~. Аксіоми й правила виводу представлені на мал. 10.

Правила мають вигляд:

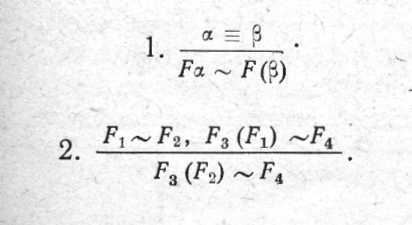
У правилах виводу над рискою записується посилка, а під рисою твердження. Буквою F позначаються довільні фрагменти, ? - порожні фрагменти; замість конюнкції в умовах ставиться яка мається на увазі крапка.

Подальше вдосконалення аксіоматики пов'язане із третім правилом виводу. Проаналізуємо його й уточнимо його зміст.

Повною умовою роботи деякої вершини V у схемі G(р₁, ..., р_k) називається логічна функція U_V, рівна одиниці на тих і тільки тих наборах значень р₁, p₂, ..., p_k, які є припустимими для вершини V. Набір Δ є припустимим для V, якщо для схеми G існує така точна конфігурація, у яку входить пара (Δ_V). Логічна функція β логічно підпорядковує розпізнавач R(α), якщо для β тотожно виконується імплікація U_R →β. Виконані умови логічної підпорядкованості гарантують, що при будь-якому можливому виконанні схеми G логічна умова α буде обчислюватися тільки для таких Δ, для яких β(Δ) = 1, що й дозволяє замінити α на β*.

* Деякий розпізнавач R(a)підпорядкован логічнії функції β, якщо перевірка Rα при виконанні схеми провадиться тільки для тих значень логічних змінних, на яких ? істина.

Застосування будь-якого правила виводу припускає попередню перевірку його посилки. «Простота» цієї перевірки є основною вимогою при побудові елементарних перетворень. Поняття простоти не уточнюється, оскільки перевірка посилок звичайно провадиться змістовними засобами. Звичайно вважається, що критерій «простоти» витриманий, якщо процес перевірки посилки зводиться до з'ясування графічного збігу або розбіжності конструктивних об'єктів, що згадують у правилі виводу. Правила виводу 1 й 2 задовольняють цьому інтуїтивному поданню про простоту, оскільки при спробі застосувати правило 2 до двох відношень рівносильності F₁~F₂ й F₃ ~ F₄ потрібно тільки виявити, чи міститься F₁ в F₃, а для застосування правила 1 потрібно виявити тотожність функцій αіβ, що легко зробити, якщо вважати, що αіβ представлені в нормальній формі. Якщо ж відмовитися від обмежень на форму подання αіβ, те все-таки цей процес може бути формалізований за допомогою аксіоматики.

Для застосування правила 3 необхідно знати для будь-якого розпізнавача R повну умову його роботи U_R. Для знаходження U_R Яновим запропонований відповідний алгоритм. Таким чином, хоча застосування правила 3 є в принципі ефективним, проте воно в деякому змісті некоректне, тому що явно не задовольняє критерію «простоти» його застосування.

О скільки знання повних умов роботи розпізнавачів є необхідним етапом перетворень операторних схем Янова, єдиною можливістю вдосконалити правило 3 є формалізація процесу побудови повних умов роботи для того, щоб ці умови з'являлися в преутвореній схемі як результат застосування аксіом і правил виводу. Для цього правило 3 заміняється чотирма новими аксіомами й одним правилом виводу. Правила 1 й 2 залишаються без змін, аксіоми І—VII піддаються незначній стилістичній переробці. Остаточний вид аксіом і правил на мал. 11.

Досліджуємо зміст цієї аксіоматики. Логічні аксіоми постулюют зв'язок базисних логічних функцій (нуль, заперечення й диз'юнкція) із правилами вибору стрілок при виконанні розпізнавачів. Їхня справедливість очевидна. Топологічні аксіоми постулюют можливість певних топологічних змін схеми (тобто змін з'єднань між вершинами схеми й усунення вершин). Аксіома 4 стверджує, що оператор без входу може бути усунутий, аксіома 5 постулюе еквівалентність порожніх періодів, аксіома 6 постулюе збереження значень логічних змінних при русі по розпізнавачах схеми. Аксіоми розподілу наборів формалізують поняття допустимості набору для розпізнавача або перетворювача схеми. Будемо трактувати логічні функції f(?) як множини тих наборів А, на яких f(?) = 1. Аксіоми групи III задають правила позначення стрілок операторної схеми деякими логічними функціями, що представляють ті набори, які можуть «проходити» уздовж стрілок при побудові конфігурацій схеми.

Аксіома 7 носить службовий характер, задаючи «початкове значення» мітящих функцій у вигляді порожньої множини наборів. Аксіома 8 постулюе той факт, що на вхідну стрілку операторної схеми може бути поданий будь-який набір. Аксіома 9 стверджує, що якщо на вхід розпізнавача з умовою α потрапляє деяка множина наборів φ, то воно повністю проноситься на виходи розпізнавача; при цьому ті набори з φ, на яких α = 1, проносяться на плюс-стрілку, а інші — на мінус-стрілку. Аксіома 10 стверджує, що якщо на вхід оператора А зі зсувом Р попадає множина наборів φ, те вона породжує на виході А множину всіх наборів, що може відрізнятися від наборів з φ тільки значеннями змінних, вхідних у зсув Р.

З аксіом розподілу наборів видно, що при позначці стрілок схеми єдиним безумовним джерелом наборів значень логічних змінних є вхідна стрілка. Аксіома 9 переносить на вихідні стрілки лише ті набори, які надходять на вхід розпізнавача. Аксіома 10 породжує лише ті набори, які можуть вийти з наборів, що надходять на вхід оператора,застосуванням операції узяття максимуму (помітимо, що max (0) =0 для будь-якого Р). Таким чином, якщо в результаті р

застосування аксіом 7—10 на стрілці s, що веде до деякої вершини операторної схеми, з'явилася множина наборів, те це значить, що кожний із цих наборів міг з'явитися на стрілці 5 лише в результаті застосування аксіом 7—10 до ланцюжка фрагментів схеми, що утворюють шлях від вхідної стрілки до вершини V.

Оскільки операторна схема в цілому є частковим випадком поняття фрагмента, розглянута аксіоматика дозволяє виводити співвідношення рівносильності для операторних схем. Властивості рівносильності як деякого бінарного співвідношення виражає наступна лема. Відношення рівносильності є рефлексивним, симетричним і транзитивним.

Доказ. Рефлексивність слідуе із правила 1 при однакових . Симетричність слідуе із правила 2, якщо як посилку взяти наступні співвідношення: F₁~F₂, F₁~F₁. Доказ транзитивності вимагає в якосты посилки співвідношення F₁~F₂, F₂~F₃. По симетричності цю посилку можна переписати у вигляді F₂~F₁ F₂~F₃, звідки за правилом 2 випливає, що F₁~F₃.

Формальну можливість трактувати розглянуту аксіоматику як правила перетворення операторних схем представляє наступна лема (правило підстановки): якщо F₁~F₂, то F(F₁) ~F(F₂).

Доказ. Взявши в правилі 2 як посилку F₁~F₂, F(F₁) ~F(F₁), одержимо, що F(F₂) ~F(F₁), звідки в силу симетричності випливає твердження леми.

Тяким чином, справедлива наступна теорема: будь-які дві рівносильні операторні схеми Янова еквівалентні.