4. Пример

I. Откроем задание к примеру (стр. 42) и построим интервальный вариационный ряд. Объем выборки n = 280; число интервалов k = 10.

1. Просматривая выборку, находим

х_min = 3,483; х_max = 5,717.

Размах выборки ∆ = 5,717  (3,483) = 9,2. Длина каждого интервала .

2. Запишем каждый из 10 интервалов (табл. 1).

3. Подсчитаем методом «конвертиков» абсолютные частоты n_i, число выборочных данных, попадающих в каждый интервал, просматривая результаты наблюдений. Убедимся, что сумма всех частот равна 280: .

Шкала интервалов и группировка результатов наблюдений методом «конвертиков» приведены в табл. 1.

Таблица 1

№	Интервал	Рабочее поле	ni
1	[3,483; 2,563)		2
2	[2,563; 1,643)		11
3	[1,643; 0,723)		24
4	[0,723; 0,197)		31
5	[0,197; 1,117)		45
6	[0,117; 2,037)		68
7	[2,037; 2,957)		50
8	[2,957; 3,877)		31
9	[3,877; 4,797)		14
10	[4,797; 5,717]		4

4. Найдем центры каждого интервала по формуле

Данные вычислений занесем в табл. 2.

5. Вычислим для каждого интервала относительные частоты

и плотность относительных частот .

Убедимся, что сумма всех относительных частот равна единице:

.

Данные вычислений занесем в табл. 2.

Таблица 2

№	Интервал		ni
1	[3,483; 2,563)	3,023	2	0,007	0,008
2	[2,563; 1,643)	2,103	11	0,039	0,042
3	[1,643; 0,723)	1,183	24	0,085	0,092
4	[0,723; 0,197)	0,263	31	0,111	0,12
5	[0,197; 1,117)	0,657	45	0,161	0,175
6	[0,117; 2,037)	1,577	68	0,243	0,264
7	[2,037; 2,957)	2,497	50	0,179	0,195
8	[2,957; 3,877)	3,417	31	0,111	0,12
9	[3,877; 4,797)	4,337	14	0,050	0,054
10	[4,797; 5,717]	5,257	4	0,014	0,015

6. Построим гистограмму (рис. 1) и полигон относительных частот (рис. 2).

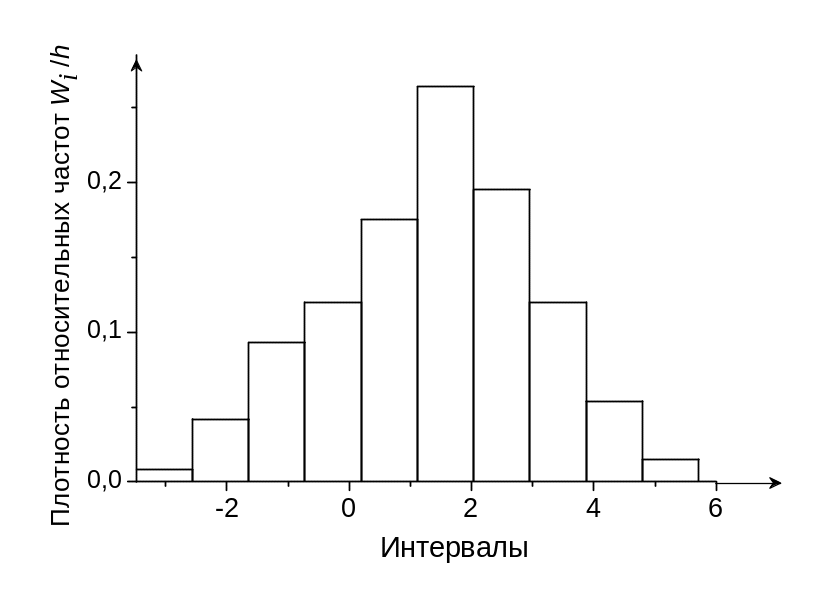
Рис. 1

Рис. 2

II. Составим выборочную функцию распределения используя вариационный ряд относительных частот:

x ≤ 3,483 = 0;

х  3,483; 2,563 = W₁ = 0,007;

х  2,563; 1,643 = W₁ + W₂ = 0,046;

х  1,643; 0,723 = W₁ + W₂ + W₃ = 0,132;

х  0,723; 0,197 = W₁+W₂ + W₃ + W₄ = 0,243;

х  0,197; 1,117 ) = W₁ +W₂ +W₃ + W₄ + W₅ = 0,404;

х  1,117; 2,037 = W₁+W₂+W₃+W₄+W₅+W₆= 0,646;

х  2,037; 2,957 ;

х  2,957; 3,877 ;

х  3,877; 4,797 ;

х  4,797; 5,717 ;

x > 5,717 .

Запишем функцию :

IV. Построим график функции (рис. 3).

Рис. 3

III. Найдем числовые характеристики наблюдаемой случайной величины:

1.  выборочное среднее по всей выборке.

2. Среднее значение по сгруппированным данным

3. Вычислим дисперсию по сгруппированным данным:

Среднее квадратическое отклонение по сгруппированным данным

4. Относительная погрешность в вычислении среднего за счет замены выборки вариационным рядом

.

IV. Выдвигаем гипотезу о законе распределения генеральной совокупности.

Сравнивая полигон относительных частот (рис. 4) с видом графиков плотности распределения f (x) для основных непрерывных распределений (рис. 13), выдвигаем гипотезу, что случайная величина имеет нормальное распределение с параметрами m (математическое ожидание) и σ (среднее квадратическое отклонение).

Рис. 4

V. Оценим параметры предполагаемого распределения и запишем его закон.

1. Оценим числовые характеристики исследуемой непрерывной случайной величины, используя оценки выборочных характеристик случайной величины Х:

математическое ожидание

«исправленную дисперсию»

.

2. Согласно выдвинутой гипотезе о нормальном распределении случайной величины, запишем параметры данного распределения с учетом точечных оценок числовых характеристик предполагаемого распределения. Для нормального распределения – два параметра:

, .

3. Запишем гипотетические функции плотности распределения f(x) и F(x), т. е. функции, соответствующие выдвинутой гипотезе о нормальном распределении:

;

,

где  функция Лапласа.

4. С помощью формул, соответствующих нормальному закону распределения, вычислим теоретические вероятности попадания случайного признака в каждый из 10 интервалов:

.

Значения функции Лапласа взяты с помощью таблицы (прил. 1).

5. Найдем ожидаемые абсолютные частоты (теоретические) для данного закона распределения: Полученные данные оформим в виде табл. 2.

Таблица 2

Номер интервала		Рi
1	3,023	0,008	2,324	0.0087
2	2,103	0,028	7,98	0.0304
3	1,183	0,072	20,3	0.0783
4	0,263	0,133	37,3	0.1446
5	0,657	0,195	54,68	0.2120
6	1,577	0,207	58,13	0.225
7	2,497	0,173	48,49	0.1881
8	3,417	0,107	29,87	0.1163
9	4,337	0,049	13,664	0.0532
10	5,257	0,017	4,872	0.0185

Рис. 5.

6. Построим на одном графике (рис. 5) полигон относительных частот статистического распределения (кривая 1) (ломаная с вершинами в точках ) (рис. 4) и гипотетическую теоретическую плотность распределения, приближенно построенную по 10 точкам (кривая 2), (ломаная с вершинами в точках ).

Из графика видно, что теоретическая кривая распределения f(x), сохраняет в основном существенные особенности статистического распределения.

VI. Проведем статистическую проверку выдвинутой гипотезы.

1. Вычислим меру расхождения  между теоретическим и статистическим распределениями по критерию Пирсона:

²_наб =

²_наб = 7,162.

2. Найдем по таблице (прил. 3) ² критическое (²_кр). Уровень значимости примем α = 0,05; число степеней свободы r = k  q  1 = 10  2  1 = 7 (здесь k – число интервалов, q – число параметров предполагаемого распределения (q = 2). По входным параметрам таблицы (α = 0,05; r = 7) находим ²_кр = 14,1.

3. Из сравнения  и  делаем вывод о правдоподобии гипотезы. Т. к. ²_наб < ²_кр, то экспериментальные данные не противоречат выдвинутой гипотезе, что случайная величина, представленная выборкой, имеет нормальный закон распределения.

В результате выполненной работы на основе статистического материала получены закон распределения, эмпирическая функция распределения и числовые характеристики вариационного ряда. Вы научились подбирать плотность распределения непрерывной случайной величины, имея лишь выборку этой случайной величины. Кроме того, оценив параметры предполагаемого распределения, вы смогли проверить их соответствие наблюдаемым результатам. Именно с такой задачей сталкиваются на практике специалисты, применяющие методы математической статистики.