1. Краткие сведения из теории

математической статистики

Математическая статистика – наука, изучающая закономерности массовых случайных явлений, базируясь на статистических данных – результатах наблюдений. Первая задача математической статистики – указать способы сбора и группировки (если данных очень много) статистических сведений. Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования.

Теория вероятностей изучает математические модели случайных явлений. Математическая статистика решает обратные задачи: разрабатывает различные методы, позволяющие по статистическим данным, которые носят случайный характер, подобрать подходящую теоретико-вероятностную модель.

Обычно изучается некоторый признак (количественный или качественный), значения которого случайны и носят название «варианта». Варианты, как и случайные величины, могут характеризоваться дискретным изменением признака или непрерывным.

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.

Выборочной совокупностью (или просто выборкой) называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка. Генеральная совокупность может быть как счетным (конечным или бесконечным) множеством, так и множеством непрерывного типа.

Число объектов выборочной совокупности называется объемом выборки.

Выборка должна быть репрезентативной (представительной), т. е. она должна достаточно полно отражать особенности всех объектов генеральной совокупности.

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно, при этом все объекты имеют одинаковую вероятность попасть в выборку.

Пусть для изучения количественного (дискретного или непрерывного) признака Х произведено n испытаний в одинаковых условиях (из генеральной совокупности извлечена выборка объема n).

Производить анализ с помощью выборки, если ее объем достаточно большой, неудобно, поэтому производят группировку статистического материала.

Для дискретного признака Х производят дискретную группировку, т. е. составляют таблицу, включающую в порядке возрастания значения вариант х_i (без повтора) и соответствующие абсолютные частоты n_i (число наблюдений) этих значений (сумма всех частот равна объему выборки n). Можно составлять таблицу из значений вариант и их относительных частот (отношение частоты n_i к объему выборки n), при этом сумма всех относительных частот равна единице. Такие таблицы называются вариационными рядами или статистическим распределением.

В целях наглядности используется графическое изображение вариационного ряда – полигон частот или полигон относительных частот. Для его построения на оси ОХ откладывают значения вариант х_i и восстанавливают перпендикуляры, равные по длине частотам n_i или относительным частотам W_i данных вариант. Концы соседних перпендикуляров соединяют отрезками. Полученная фигура – полигон.

Для непрерывно изменяющегося признака используют интервальную группировку: весь интервал значений вариант разбивают на конечное число граничащих друг с другом равных интервалов. На практике число интервалов в группировке берут (точных формул для подсчета k нет, есть лишь некоторые рекомендации: и другие). Совокупность расположенных в порядке возрастания интервалов вариации длины h и частот вариант n_i (количество элементов выборки, попавших в соответствующий интервал) либо относительных частот вариант (отношение частоты к объему выборки), попавших в соответствующий интервал, называется интервальным (группированным) вариационным рядом, статистической совокупностью или статистическим распределением.

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами или интервалами значений вариант и их частотами, или относительными частотами.

Графически интервальный вариационный ряд изображается в виде гистограммы частот или гистограммы относительных частот (ступенчатый график). Для гистограммы частот на оси абсцисс откладывают интервалы значений признака длины h и на каждом из них, как на основании, строят прямоугольник с высотой (плотность частоты). Площадь частичного i-го прямоугольника равна – частоте вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот (объему выборки n).

Для гистограммы относительных частот на оси абсцисс откладывают интервалы значений признака длины h и на каждом из них, как на основании, строят прямоугольник с высотой (плотность относительной частоты). Площадь частичного i-го прямоугольника равна – относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице. При увеличении объема выборки и уменьшении длины интервала группировки гистограмма относительных частот является статистическим аналогом плотности распределения генеральной совокупности.

Иногда интервальный вариационный ряд для простоты исследований условно заменяют дискретным. В этом случае середину i-го интервала принимают за варианту х_i, а соответствующую интервальную частоту n_i – за частоту интервала. В этом случае для графического изображения интервального вариационного ряда можно использовать полигон. Полигоном относительных частот называется ломаная линия с вершинами в точках . Если плотность распределения генеральной совокупности является достаточно гладкой функцией, то полигон относительных частот является более хорошим приближением плотности, чем гистограмма.

Дальнейшую обработку статистического материала проводят на основе вариационных рядов. С их помощью составляют – статистическую функцию распределения выборки, которая называется эмпирической и задает для каждого значения х относительную частоту события (X<x):

, где n – объем выборки, n_x – число выборочных значений величины Х, меньших х.

В отличие от эмпирической функции распределения выборки , интегральную функцию F(x) распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что F(x) определяет вероятность события (X<x), в то время как определяет относительную частоту этого события при проведении n экспериментов. При достаточно большом объеме выборки эмпирическую функцию распределения можно рассматривать как статистический аналог распределения всей генеральной совокупности.

Продолжая анализ статистического материала, можно выделить некоторые постоянные, которые представляли бы вариационный ряд в целом и отражали присущие всей совокупности закономерности. Такие числовые характеристики называют эмпирическими. В первую очередь к ним относятся: выборочное среднее (центр распределения признака), вокруг которого концентрируются результаты наблюдений, и выборочная дисперсия, характеризующая разброс значений вокруг центра.

Выборочной средней называется среднее арифметическое значений признака выборочной совокупности.

Если все значения различны, то

.

Если же значения признака имеют соответственно частоты , то

Выборочной дисперсией называется среднее арифметическое квадратов отклонения наблюдаемых значений выборки от их среднего значения .

Если все значения различны, то

Если же значения признака имеют соответственно частоты , то

.

Вычисление выборочной дисперсии можно упростить, используя следующую теорему: дисперсия равна среднему квадратов значений признака минус квадрат общей средней.

Если все значения различны, то

.

Если же значения признака имеют соответственно частоты , то

.

Кроме дисперсии, для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением, которое выражается в тех же единицах, что и значения признака и выборочной средней.

Выборочным средним квадратическим отклонением называется арифметический квадратный корень из выборочной дисперсии: .

Рассмотрим основные законы распределения непрерывных случайных величин.

Равномерным называют распределение вероятностей непрерывной случайной величины Х, если на отрезке [a,b], которому принадлежат все возможные значения Х, плотность постоянна, т. е

где числа a и b – параметры равномерного распределения.

График плотности вероятности равномерного распределения изображен на рис. 1.

Функция распределения для равномерного распределения имеет вид:

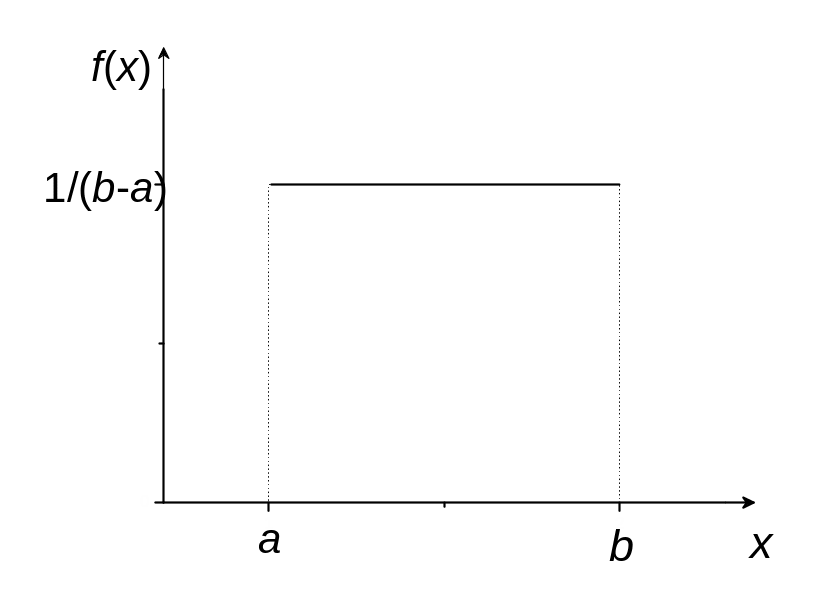
Рис. 1

Математическое ожидание М(Х) равномерно распределенной на отрезке [a,b] случайной величины Х совпадает с серединой отрезка [a,b] и равно

.

Дисперсия D(X) равна

,

откуда следует, что среднее квадратическое отклонение

Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (α, β), принадлежащий целиком отрезку [a,b], равна

.

Нормальным называют распределение вероятностей непрерывной случайной величины Х, если плотность распределения имеет вид:

,

где числа m и σ – два параметра нормального распределения.

График плотности вероятности нормального распределения изображен на рис. 2.

Функция распределения для нормального распределения имеет вид

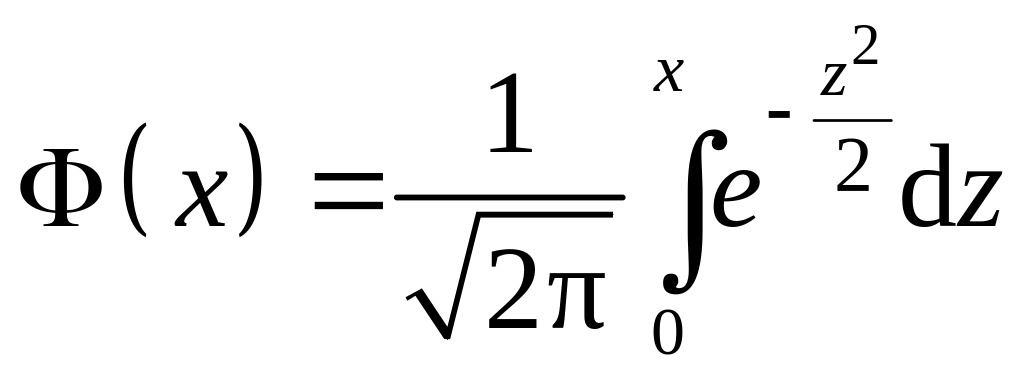, где – функция Лапласа. Таблица значений функции Лапласа дана в прил. 1.

Математическое ожидание М(Х) нормально распределенной случайной величины Х равно параметру нормального распределения m, т. е.

.

Дисперсия D(X) равна квадрату параметра нормального распределения σ, т. е.

,

откуда следует, что среднее квадратическое отклонение σ_х равно параметру σ:

.

Вероятность попадания значения случайной величины, имеющей нормальное распределение, в заданный интервал (α, β) можно выразить через функцию Лапласа:

.

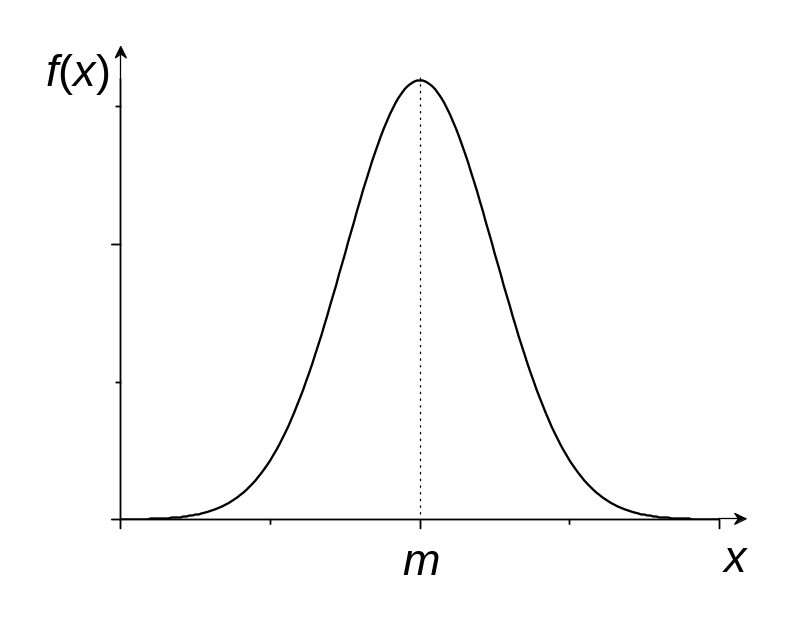
Рис. 2

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

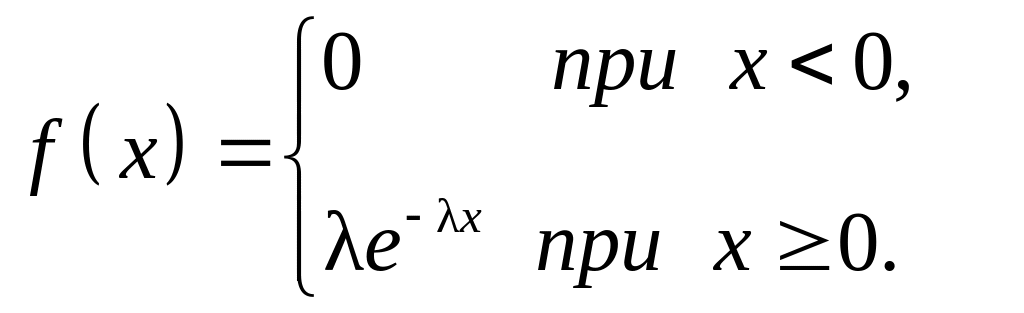
где λ – постоянная положительная величина. Показательное распределение определяется только одним параметром λ.

График плотности вероятности показательного распределения изображен на рис. 3.

Функция распределения для показательного распределения имеет вид:

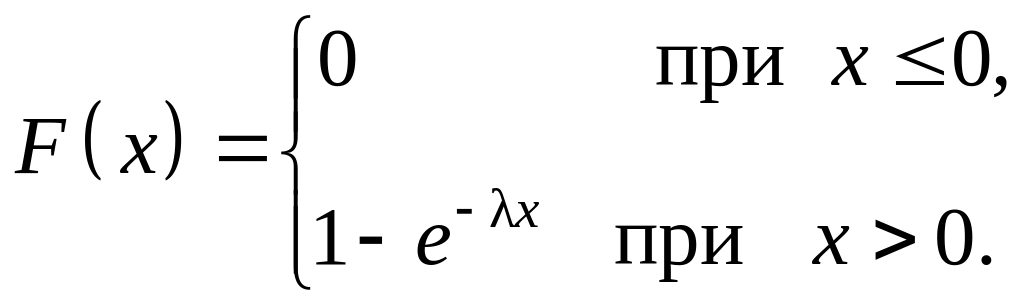
Для показательного распределения математическое ожидание М(Х), дисперсия D(X) и среднее квадратическое отклонение σ_х равны, соответственно:

Таким образом, для показательного распределения характерно, что среднее квадратическое отклонение численно равно математическому ожиданию.

Вероятность попадания значения случайной величины, имеющей показательное распределение, в заданный интервал (α, β), равна

Рис. 3