
- •Учебная программа дисциплины
- •2. Данные о дисциплине:
- •Пререквизиты:
- •Краткое описание дисциплины
- •График выполнения и сдачи заданий по дисциплине
- •1.7 Список литературы
- •1.8 Оценка знаний согласно шкале рейтинга
- •1.9 Политика и процедура
- •Учебно-методические материалы по дисциплине
- •2.3 Планы практических занятий
- •Оценка участия в семинарах
- •Планы домашних заданий
- •Содержание домашних заданий
- •Оценка домашних заданий
- •Планы занятий в рамках самостоятельной работы студентов под руководством преподавателя Содержание заданий для срсп
- •Оценка заданий для срсп
- •Планы занятий в рамках самостоятельной работы студентов
- •Вопросник для коллоквиума
- •Матрицы и операции над ними.
- •Определители и их свойства.
- •Системы линейных алгебраических уравнений.
- •Векторы. Линейные операции над векторами.
- •Нелиейные операции над векторами. Метод координат
- •Прямая на плоскости.
- •Кривые 2-го порядка.
- •Уравнение плоскости.
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве.
- •Функция. Действительные числа. Предел функции. Односторонние пределы функции.
- •Элементарные функции
- •Предел функции. Основные теоремы о пределах
- •Замечательные пределы. Сравнение бесконечно малых функций. Широко используются следующие два предела
- •Непрерывность функции. Классификация точек разрыва функции.
- •Производная. Правила и формулы дифференцирования.
- •Производные высших порядков. Дифференциалы первого и высших порядков и их приложения.
- •Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши). Правило Лопиталя. Приложения производной и исследование функции.
- •Исследование поведения функции и построение их графиков.
- •Выпуклость графика функции. Точки перегиба
- •Асимтоты.
- •Первообразная. Неопределенный интеграл и его свойства.
- •Интегрирование рациональных функций.
- •Интегрирование иррациональных и трансцендентных функций.
- •Определенный интеграл. Условия существования определенного интеграла. Свойства определенного интеграла.
- •Проведя в точках деления a,b прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки 1,2,…,т, так что
- •Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле.
- •Приложения определенного интеграла.
- •Частные производные и дифференцируемость функций нескольких переменных.
- •Частные производные высших порядков
- •Лекции 29. Дифференциальные уравнения. Дифференциальные уравнения I порядка.
- •Линейные дифференциальные уравнения второго порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Числовые ряды.
- •Признаки сходимости рядов
- •Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды.
- •Свойства степенных рядов.
- •Двойные и тройные интегралы.
- •Векторные и скалярные поля
- •Криволинейные интегралы
- •Случайные события. Определение вероятности.
- •Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса.
- •Формула Бернулли. Предельные теоремы.
- •Случайные величины и их числовые характеристики.
- •Задачи математической статистики. Выборочный метод. Эмпирическая функция распределения. Полигон и гистограмма.
- •Параметры распределения.
- •Точечные и интервальные оценки.
- •Элементы теории корреляции.
- •Статистическая проверка статистических гипотез.
Оценка интеграла. Теорема о среднем. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле.
В данном разделе рассмотрим оценки определенных интегралов, а также формулу Ньютона-Лейбница позволяющую вычислять определенный интеграл.
Теорема 1 (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е.
m(b-a)<![]() <M(b-a),
a<b,
<M(b-a),
a<b,
где m и M- соответственно наименьшее и набольшее значения функции f(x) в интервале a;b.
Теорема 2. Если в каждой точке x интервала a;b
(x)f(x)(x),
то
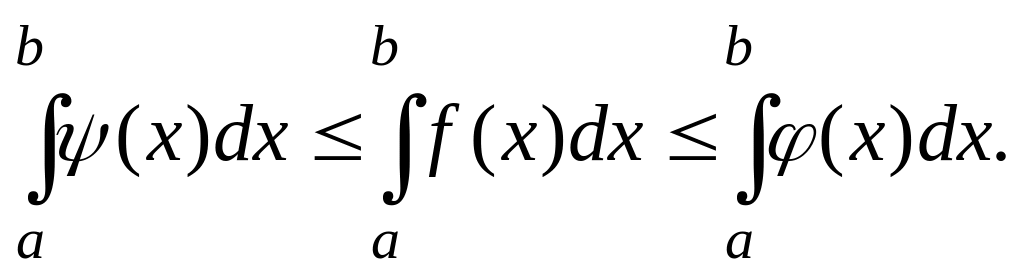
Теорема 3 (о среднем). Внутри интервала интегрирования a;b существует хотя бы одно значение x=,, для которого
![]()
![]() .
.
Формула Ньютона – Лейбница.
Теорема 4. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла:
![]() ,
где F(x)=f(x) (2)
,
где F(x)=f(x) (2)
Равенство (2) называется формулой Ньютона – Лейбница.
Пример.
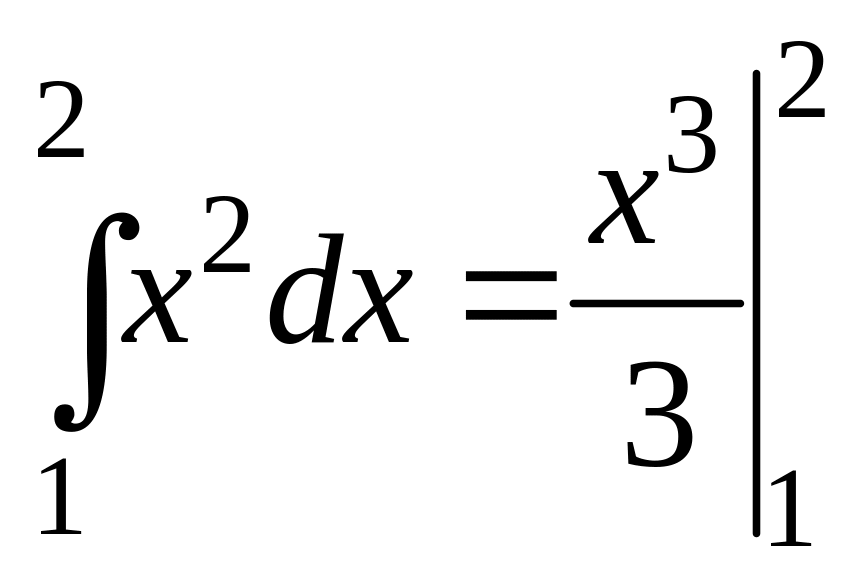 =
=![]() .
.
Интегрирование по частям и замена переменной в определенном интеграле.
1. Формула интегрирования по частям:
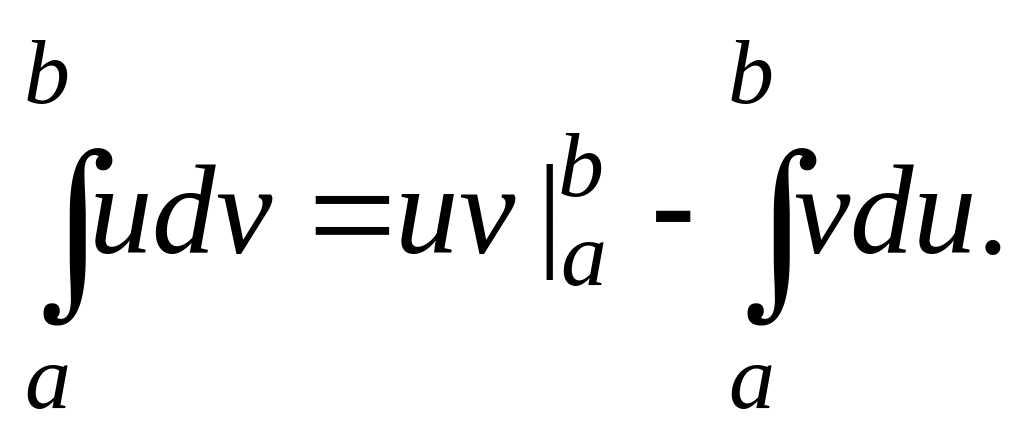
Формула замены переменной (подстановки):
Пусть x=(u), тогда справедлива формула
![]()
Если в интервале u1, u2 функции x=(u), (u) и (u) непрерывны и (u1)=x1, (u2)=x2, то
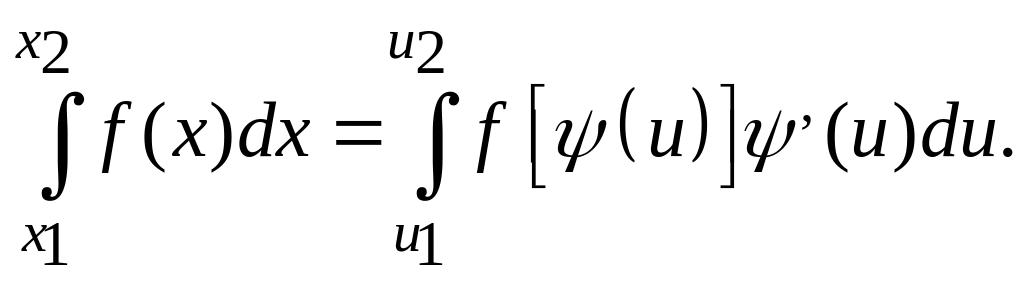
Несобственные интегралы.
Когда нами было введено понятие определенного интеграла, мы предполагали, что интервал интегрирования имеет конечную длину, а также необходимым условием интегрируемости является ограниченность функции. На этом занятии мы обобщим понятие определенного интеграла на случаи неограниченного интервала интегрируемости и на случай неограниченной функции. Такие интегралы называются несобственными интегралами. Интеграл по неограниченному промежутку интегрирования называется несобственным интегралом I рода, а интеграл от неограниченной функции – несобственным интегралом II рода.
Несобственным интегралом от функции f(x) в интервале a называется предел интеграла при b, то есть
![]() .
.
Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.
С помощью формулы Ньютона – Лейбница получаем
![]() F(b)F(a)=F()F(a)
на интервале a,),
F(b)F(a)=F()F(a)
на интервале a,),
![]() F(a)F(-)
на интервале a.
F(a)F(-)
на интервале a.
Если функция f(x) определена и непрерывна на всей числовой оси, то можно рассматривать несобственный интеграл в интервале ()
![]() .
.
Если
оба интеграла в правой части сходятся,
то интеграл
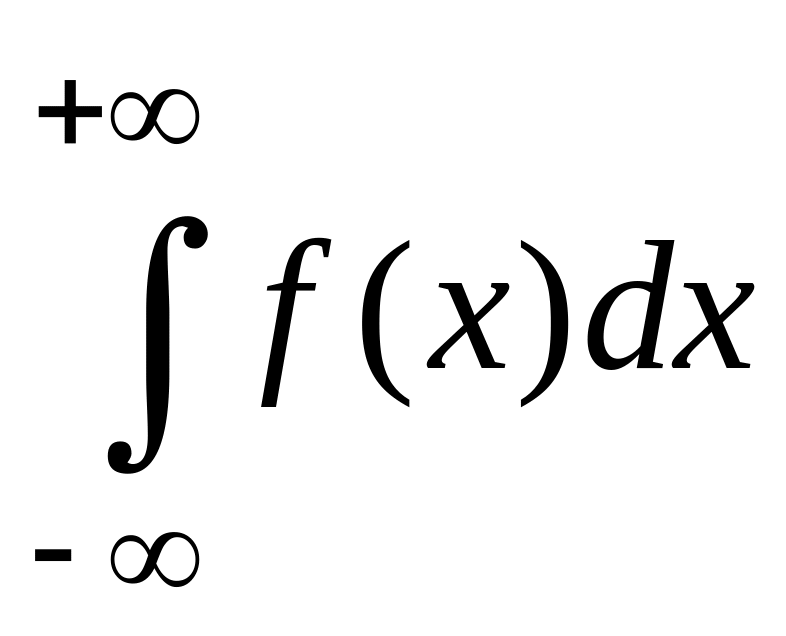 называется
сходящимся.
называется
сходящимся.
Если первообразная F(x) известна, то
=F()F(),
где
F(+)=![]() ,
F()=
,
F()=![]() .
.
Если хотя бы один из этих пределов не существует, то несобственный интеграл расходится.
Пример.
Интеграл
![]() сходится,
так как
сходится,
так как
![]()
Интеграл
![]() расходится, так как
расходится, так как
![]()
Для исследования на сходимость интегралов можно воспользоваться следующим признаком.
Признак
сравнения.
Пусть для всех x
выполнено 0f(x)(x).
Тогда: 1) если сходится интеграл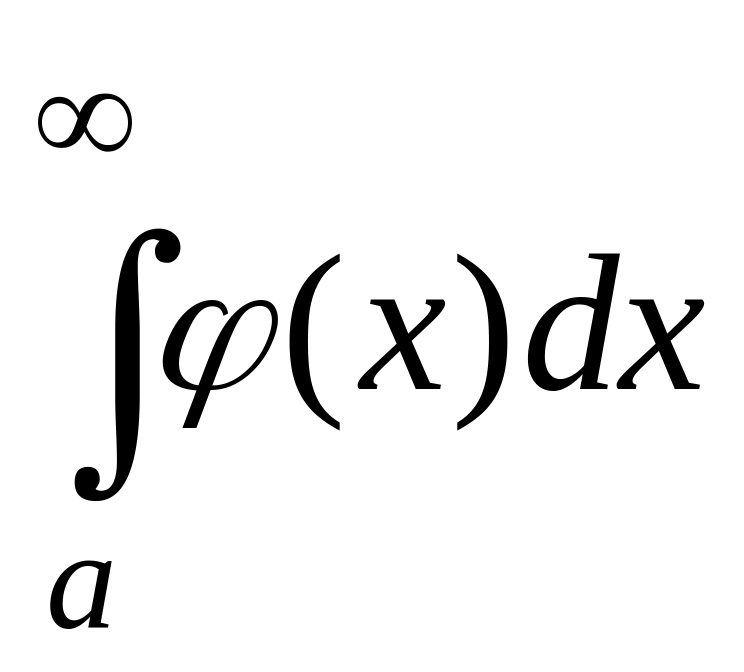 ,
то сходится и интеграл
,
то сходится и интеграл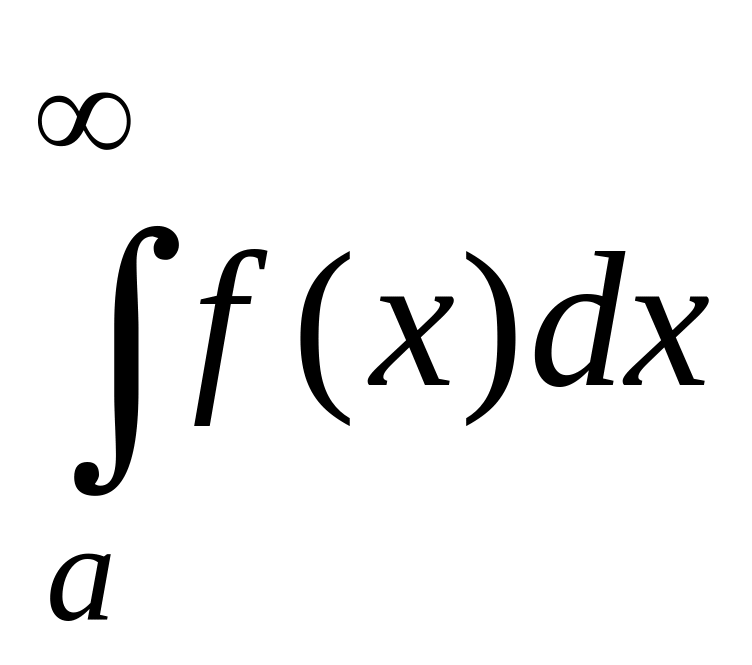 ;
;
если расходится интеграл
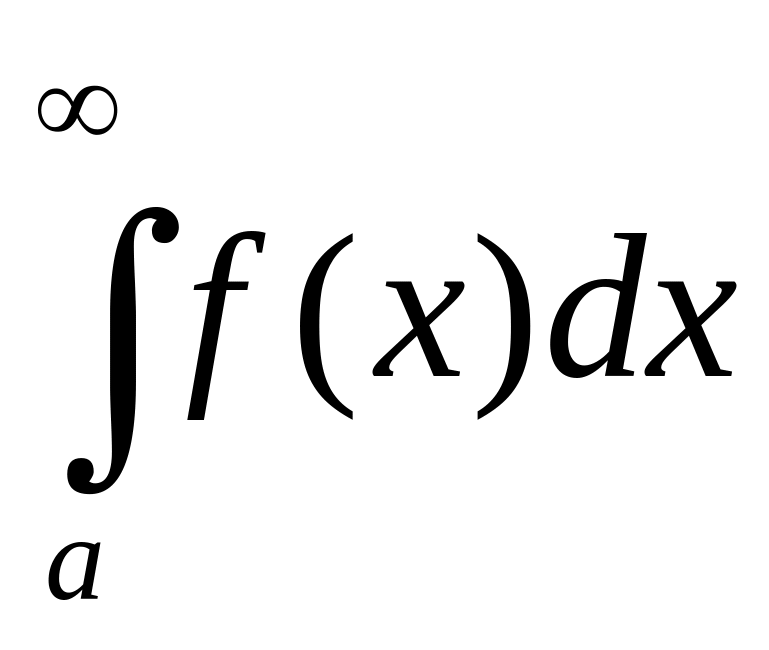 ,
то расходится интеграл
,
то расходится интеграл
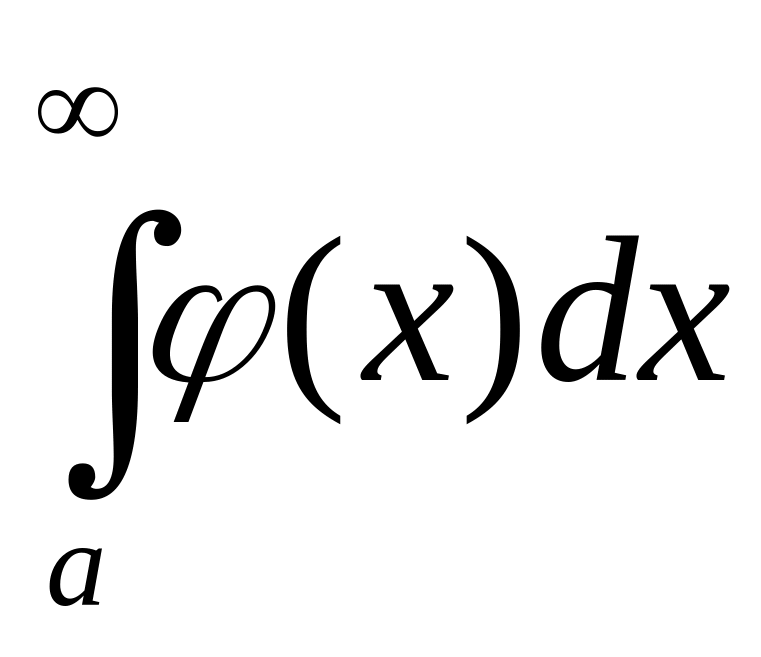 .
.
Несобственные
интегралы играют важную роль в различных
разделах математики и ее приложениях,
так, например, интеграл вида![]() называется интегралом Пуассона и играет
важную роль в теории вероятности.
называется интегралом Пуассона и играет
важную роль в теории вероятности.
Лекция 24
