Задачи по курсу «Теоретическая механика и теория поля» и их решение.

1 . Наити функцию Лагранжа двойного плоского маятника , находящегося в однородном поле тяжести (ускорение силы тяжести g).

Решение. в качестве координат берём углы φ₁ и φ₂, которые нити l₁ и l₂ образуют с вертикалью. Тогда для точки m₁ имеем:

чтобы найти кинетическую энергию второй точки, выражаем её декартовы координаты x₂, y₂ (начало координат в точке подвеса, ось y – по вертикали вниз) через углы φ₁ и φ₂:

после этого получим:

окончательно:

2 . Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m₂, точка которого (с массой m₁ в ней) может совершать движения по горизонтальной прямой.

Решение. Вводя координату x точки m₁ и угол φ между нитью маятника и вертикалью, получим:

3. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

Решение. В декартовых координатах x, y, z:

В цилиндрических координатах r, φ, z:

В сферических координатах r, θ, φ:

4. Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса материальной частицы.

Ответ: =-p_z

=0, =-p_y

5. Определить скобки Пуассона, составленные из компонент М.

Ответ: =-M_z, =-M_x , =-M_y.

6. Показать, что

=0, ,

где φ – любая скалярная функция координат и импульса частицы.

Указание. Скалярная функция может зависеть от компонент векторов r и p только в комбинациях r²,p², . Поэтому

и аналогично для .

7. Показать, что

= ,

где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.

Указание. Произвольный вектор f(r, p) может быть написан в виде где - скалярные функции

8. Выразить амплитуду и начальную фазу колебаний через начальные значения x₀, v₀ координаты и скорости.

Ответ:

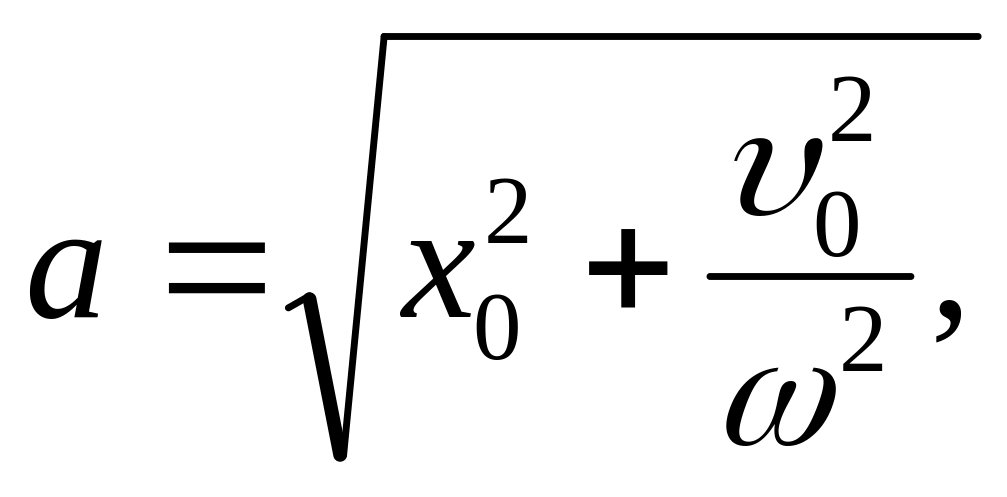
9 . Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.

Решение. Потенциальная энергия пружины (с точностью до малых величин высшего порядка) равна произведению силы F на удлинение δl пружины. при x<<l имеем:

,

так что U=Fx²/2l. Поскольку кинетическая энергия есть то

10. Найти частоту колебаний маятника, точка подвеса которого (с массой m₁ в ней) способна совершать движение в горизонтальном направлении.

Решение. При φ<<1 находим:

Отсюда

11. Определить малые колебания двойного плоского маятника.

Решение. Для малых колебаний найденная в задаче 1 параграфа 5 функция Лагранжа принимает вид :

.

Уравнения движения:

После подстановки (23,6) :

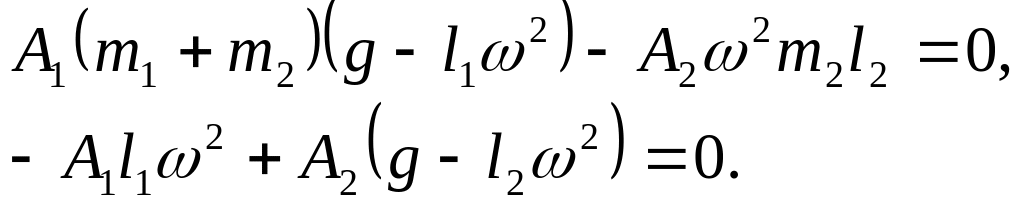
Корни характеристического уравнения:

Ответ: .

При частоты стремятся к пределам и , соответствуют независимым колебаниям двух маятников.

12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

Решение.

13. Вычислить где p – постоянный вектор.

Решение.

14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.

Решение. Умножим искомый интеграл на постоянный вектор р:

Так как вектор р произволен, то

.

Аналогично показывается, что

15. Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара . Объемная плотность заряда равна , радиус шара R.

Решение. Из принципа суперпозиции полей следует, что искомая напряженность поля равна разности напряженности электрического поля, создаваемого шаром без полости, и напряженности поля зарядов, заполняющих при этом полость.

Поле внутри полости

поле внутри шара (но вне полости)

поле снаружи шара

где - радиус-вектор, проведенный из центра шара к центру полости.

16. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

Решение. Потенциал точечного заряда является решением уравнения

(1)

Представим и в виде разложений в интеграл Фурье:

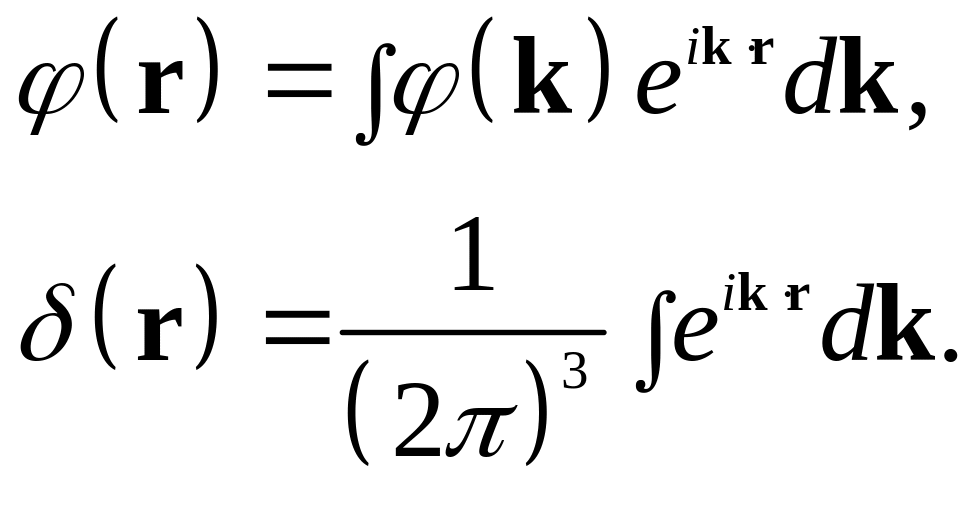(2)

Подставляя соотношения (2) в уравнение (1) и приравнивая в подынтегральных выражениях коэффициенты при , получим

.

17. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону:

Решение. .

18. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

Решение. Предположив, что заряд расположен в начале координат, решим уравнения

Направим оси декартовой системы координат по главным осям тензора диэлектрической проницаемости. Тогда

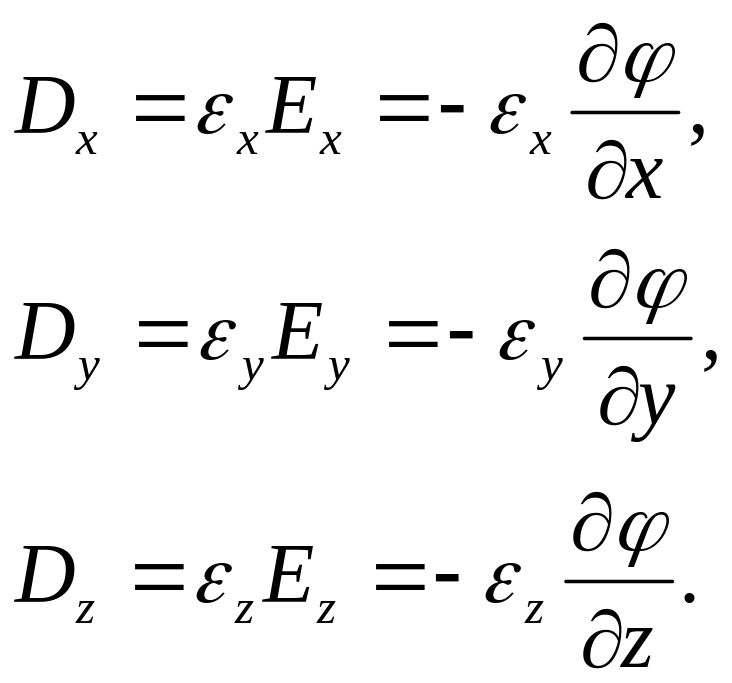
Подставим соотношения (2) в уравнение (1):

Заменой уравнение приводится к виду

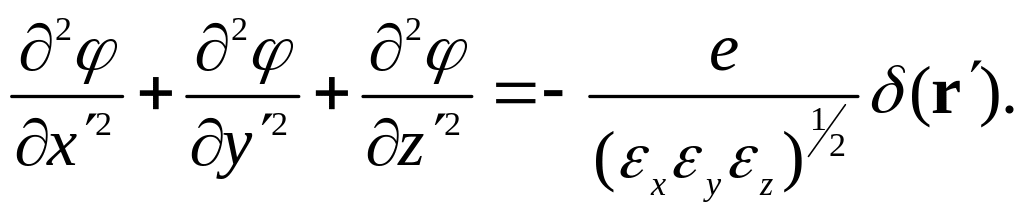
Здесь использовано свойство δ-функции:

Решение уравнения (4) имеет вид

где

19. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью j. Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

Решение. H=1/2

20. Показать, что постоянное однородное магнитное поле В можно описывать векторным потенциалом А= .

21. Найти интенсивность излучения частицы массы m, движущейся по круговой орбите радиуса а, под действием кулоновских сил. Выразить ответ через энергию частицы.

Решение. Из формулы, по которой вычисляется интенсивность дипольного излучения, где p=er, исключаем r, пользуясь уравнением движения

Отсюда

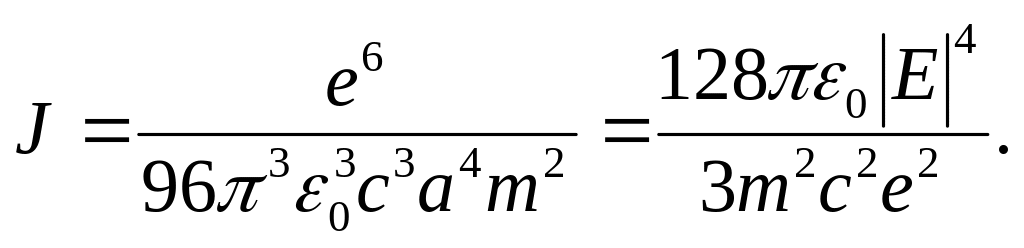
где Е – энергия частицы.