3.7. Магнитное поле соленоида и тороида
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 3.12). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (рис. 3.12, б) показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым.
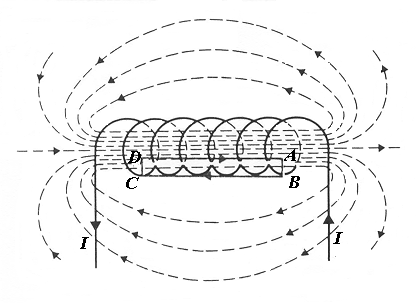
Рис. 3.12
На рис. 3.12 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его, поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 3.12. Циркуляция вектора по замкнутому контуру ABCDA, охватывающему все N витков, согласно (3.21)
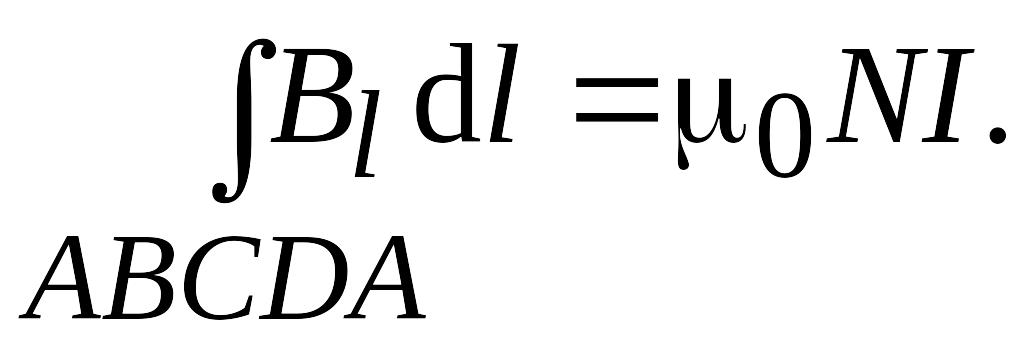
Интеграл пo ABCDA можно представить в виде четырех интегралов: по AB, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и Вl = 0. На участке вне соленоида В = 0. На участке DA циркуляция вектора равна Вl (контур совпадает с линией магнитной индукции); следовательно,
(3.24)
Из (3.24) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):
(3.25)
где I сила тока.
Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают).
Для практики также интересен расчет магнитного поля тороида – кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 3.13). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.
Линии магнитной индукции в данном случае есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиусом r. Тогда, по теореме о циркуляции (3.21),
,
откуда следует, что магнитная индукция внутри тороида (в вакууме)
(3.26)
где N – число витков тороида.
Если
контур проходит вне тороида, то токов
он не охватывает и
.
Это означает, что поле вне тороида
отсутствует (что показывает и опыт).
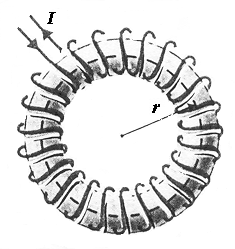
Рис. 3.13
3.8. Поток вектора магнитной индукции. Теорема Гаусса для поля
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная
(3.27)
где
–
проекция
вектора
на направление нормали к площадке dS
(
– угол между векторами
и
),
– вектор, модуль которого равен dS,
а направление совпадает с направлением
нормали
к площадке. Поток вектора
может быть как положительным, так и
отрицательным в зависимости от знака
cos .
Поток вектора магнитной индукции ФВ через произвольную поверхность S
(3.28)
Для
однородного поля и плоской поверхности,
расположенной перпендикулярно вектору
,
const
и
Единица магнитного потока – вебер
(Вб). Это магнитный поток, проходящий
через плоскую поверхность площадью 1
м2,
расположенную перпендикулярно однородному
магнитному полю, индукция которого
равна 1 Тл, равен 1 Вб (1 Вб = 1 Тлм2).
Теорема Гаусса для поля В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
(3.29)
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Итак, для потоков векторов и сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения.
В качестве примера рассчитаем поток вектора через соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью согласно (3.25)
Магнитный поток через один виток соленоида площадью S
а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,
. (3.30)