Двойственность Понтрягина

При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со сверткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляют такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.

Сходимость ряда Фурье

Обозначим через S_N(f,x) частичные суммы ряда Фурье функции f(x):

.

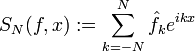Далее обсуждается сходимость последовательности функций S_N(f,x) к функции f(x) в различных смыслах. Функция f предполагается 2π-периодической (если она задана только на промежутке [ − π,π], её можно периодически продолжить).

• Если , то последовательность S_N(f,x) сходится к функции f(x) в смысле L₂. Кроме того, S_N(f,x) являются наилучшим (в смысле расстояния в L₂) приближением функции f тригонометрическим многочленом степени не выше N.

• Сходимость ряда Фурье в заданной точке x₀ — локальное свойство, то есть, если функции f и g совпадают в некоторой окрестности x₀, то последовательности S_N(f,x₀) и S_N(g,x₀) либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают.

• Если функция f дифференцируема в точке x₀, то её ряд Фурье в этой точке сходится к f(x₀). Более точные достаточные условия в терминах гладкости функции f задаются признаком Дини.

• Функция, непрерывная в точке x₀, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к f(x₀). Это следует из того, что для непрерывной в x₀ функции f последовательность S_N(f,x₀) сходится по Чезаро к f(x₀).

• Если функция f разрывна в точке x₀, но имеет пределы в этой точке справа и слева 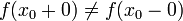, то при некоторых дополнительных условиях S_N(f,x₀) сходятся к (f(x₀ + 0) + f(x₀ − 0)) / 2. Подробнее см. модифицированный признак Дини.

• Теорема Карлесона: если , то её ряд Фурье сходится к ней почти всюду. Это верно и если 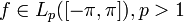. Однако, существуют функции из L₁([ − π,π]), ряд Фурье которых расходится во всех точках (теорема Колмогорова).

• Зафиксируем точку 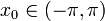. Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве C([ − π,π]). В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.

Практическая часть

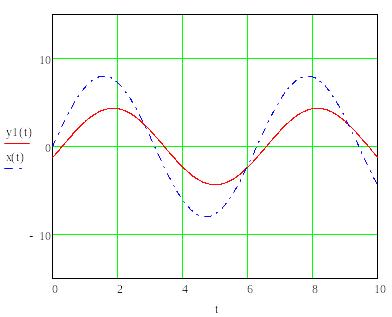
Дан сигнал аналогово-цифрового преобразователя (рис.1)

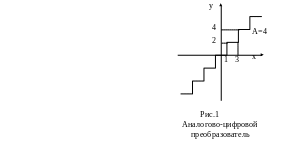
Найти амплитуду В₁ и фазу ₁ первой гармоники

y₁(t)=В₁sin(t+₁)

сигнала y(t) на выходе нелинейности.

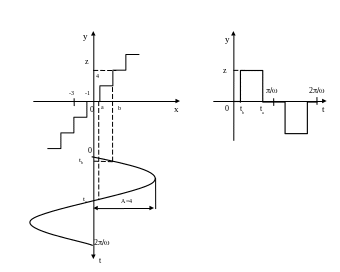
рис.2

Решение.

Способ решения основан на аналитическом описании сигнала y(t) на выходе нелинейного звена, последующем разложении y(t) в ряд Фурье и использовании из этого ряда выражения для первой гармоники.

В соответствии с рис.2 выходной сигнал y(t) представляет собою периодическую кусочно монотонную и ограниченную функцию, следовательно для нее существует ряд Фурье.

Функция y(t) имеет вид разнополярных прямоугольных импульсов с амплитудой z и моментами переключения t_a и t_b, определяемыми решениями уравнений:

(1)

или

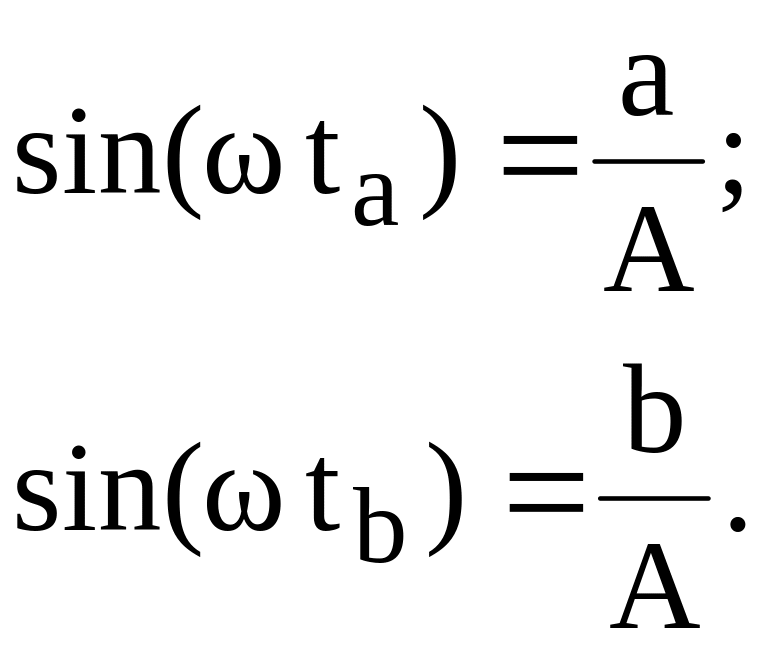
Найдем интересующие нас коэффициенты Фурье для y(t).

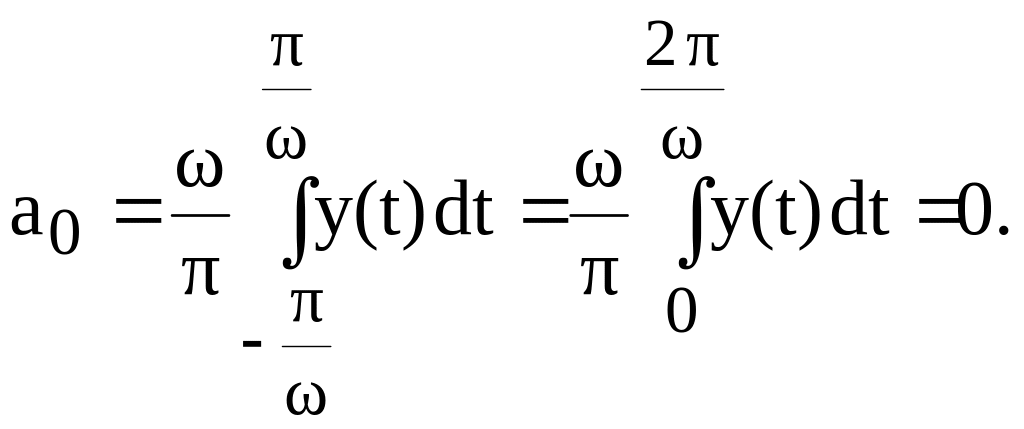
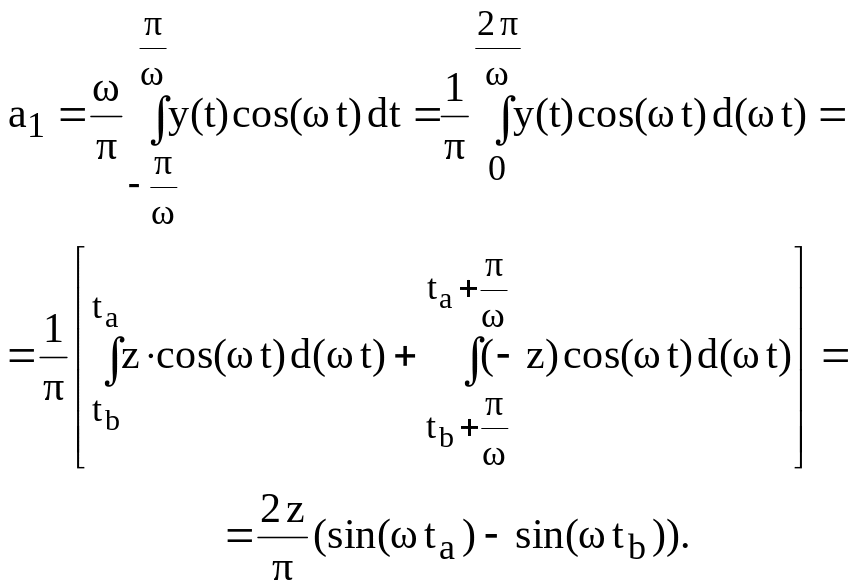
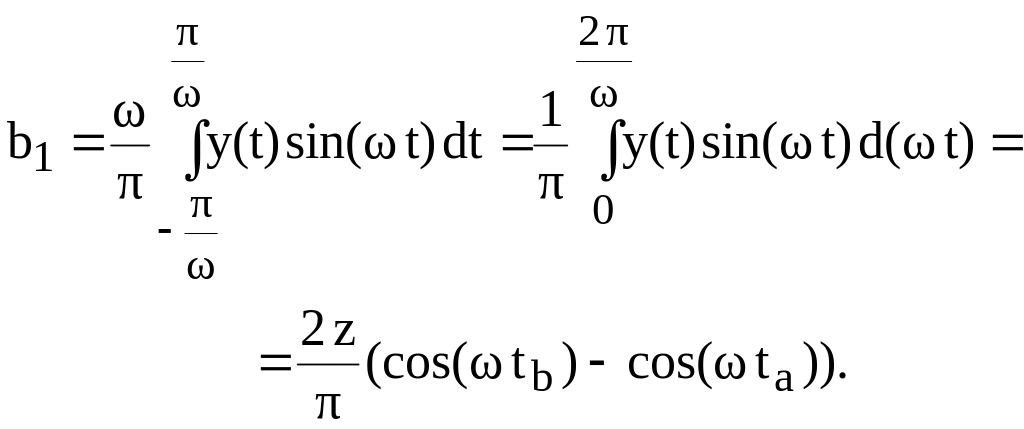
Или, с учетом (1), и для исходных данных a=1, b=3, z=4, A=4 получим

Представив первую гармонику выходного сигнала в виде

y₁(t)=B₁sin(t+₁)=a₁cos(t)+b₁sin(t),

найдем искомые величины

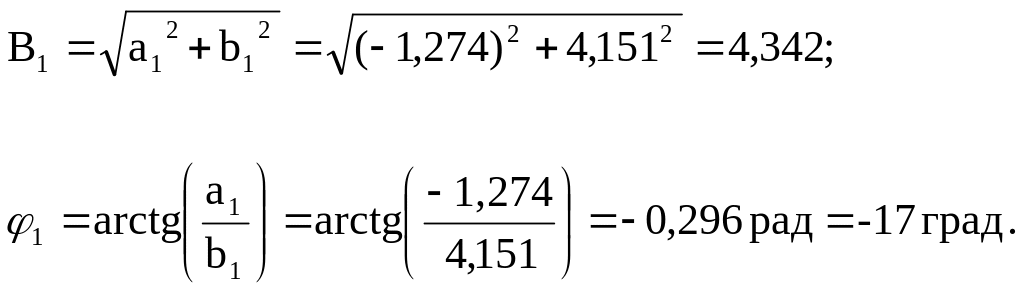
Результат решения.

Амплитуда первой гармоники сигнала на выходе нелинейности В₁ = 3,48;

фаза  = -0,31 радиана.

Заключение

Проводя анализ результатов данной работы, можно заключить следующее:

с помощью разложения в ряд Фурье возможно принципиально рассчитать качественные характеристики интересующей нас технической системы.

В данном конкретном случае наша задача есть ничто иное, как моделирование и гармонический анализ аналогово-цифрового преобразователя(АЦП), устройства которое преобразует входной аналоговый сигнал в дискретный код (цифровой сигнал).

В наше время аналогово-цифровой преобразователь нашёл себе широкое применение. Аналого-цифровое преобразование используется везде, где требуется принимать аналоговый сигнал и обрабатывать его в цифровой форме.

• Специальные видео-АЦП используются в компьютерных ТВ-тюнерах, платах видеовхода, видеокамерах для оцифровки видеосигнала. Микрофонные и линейные аудиовходы компьютеров подключены к аудио-АЦП.

• АЦП являются составной частью систем сбора данных.

• АЦП последовательного приближения разрядностью 8..12 бит и сигма-дельта АЦП разрядностью 16..24 бита встраиваются в однокристальные микроконтроллеры.

• Очень быстрые АЦП необходимы в цифровых осциллографах (используются параллельные и конвеерные АЦП)

• Современные весы используют АЦП с разрядностью до 24 бит, преобразующие сигнал непосредственно от тензометрического датчика. (сигма-дельта АЦП)

• АЦП входят в состав радиомодемов и других устройств радиопередачи данных, где используются совместно с процессором ЦОС в качестве демодулятора.

• Сверхбыстрые АЦП используются в антенных системах базовых станций (в так называемых SMART-антеннах) и в антенных решётках РЛС.

Список литературы

• Жук В.В., Натансон Г.И. Тригонометрические ряды Фурье и элементы теории аппроксимации — Л.: Изд-во Ленингр. ун-та, 1983. — С. 188.

• Рудин У. Основы математического анализа — 1976.

• Пискунов Н. С. Дифференциальное и интегральное исчисления для ВТУЗов — М.: «Наука», 1964. — Т. 2.

• Зигмунд А. Тригонометрические ряды. — М.: «Мир», 1965. — Т. 1.

2