Тригонометрический ряд Фурье

Тригонометрическим рядом Фурье функции называют функциональный ряд вида

(1)

где

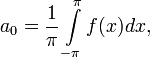
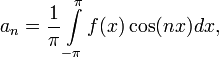
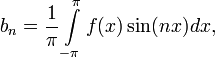
Числа a₀, a_n и b_n ( ) называются коэффициентами Фурье функции f. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию в виде ряда (1), и нам надо определить неизвестные коэффициенты a₀, a_n и b_n. Если умножить правую часть (1) на cos(kx) и проинтегрировать по промежутку [ − π,π], благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент a_k. Аналогично для b_k

Ряд (1) сходится к функции f в пространстве L₂([ − π,π]). Иными словами, если обозначить через S_k(x) частичные суммы ряда (1):

,

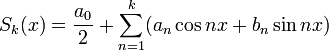то их среднеквадратичное отклонение от функции f будет стремиться к нулю:

.

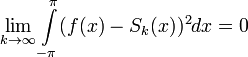Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.

Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство комплекснозначных функций со скалярным произведением

.

Мы также рассматриваем систему функций

.

Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция может быть разложена по ним в ряд Фурье:

,

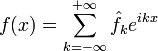где ряд в правой части сходится к f по норме в . Здесь

.

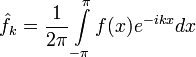Коэффициенты : связаны с классическими коэффициентами Фурье по следующим формулам:

• Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для её разложения и 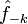не будут, вообще говоря, комплексно сопряженными.

Обобщения Ряды Фурье в гильбертовом пространстве

Описанную выше конструкцию можно обобщить со случая пространства L²[ − π,π] с тригонометрической системой на произвольное гильбертово пространство. Пусть даны ортогональная система {φ₁,φ₂,...,φ_n,...} в гильбертовом пространстве R и f — произвольный элемент из R. Предположим, мы хотим представить f в виде (бесконечной) линейной комбинации элементов {φ_k}:

Домножим это выражение на φ_k. С учётом ортогональности системы функций {φ_k} все слагаемые ряда обращаются в ноль, кроме слагаемого при n = k:

(f,φ_k) = c_k | | φ_k | | ²

Последовательность чисел

называется координатами, или коэффициентами Фурье элемента f по системе {φ_k}, а ряд

∑	ckφk
k

называется рядом Фурье элемента f по ортогональной системе {φ_k}.

Ряд Фурье любого элемента f по любой ортогональной системе сходится в пространстве R, но его сумма не обязательно равна f. Для ортонормированной системы φ_k в сепарабельном гильбертовом пространстве следующие условия эквивалентны:

• система является базисом, то есть сумма ряда Фурье любого элемента равна этому элементу.

• система является полной, то есть в R не существует ненулевого элемента, ортогонального всем элементам φ₁,φ₂,...,φ_n,... одновременно.

• система является замкнутой, то есть для любого 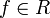выполнено равенство Парсеваля

.

• линейные комбинации элементов φ₁,φ₂,...,φ_n,... плотны в пространстве R.

Если эти условия не выполняются, то сумма ряда Фурье элемента f равна его ортогональной проекции на замыкание линейной оболочки элементов φ₁,φ₂,...,φ_n,.... В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя: