Метод Крамера

Определители играют большую роль в решениях линейных систем из уравнений относительно неизвестных

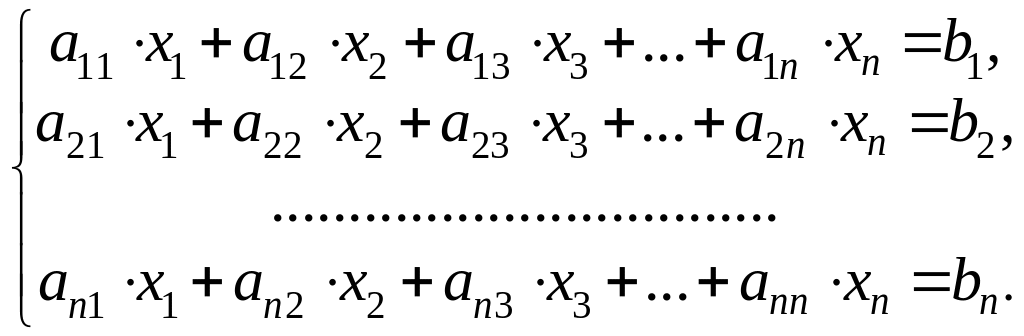
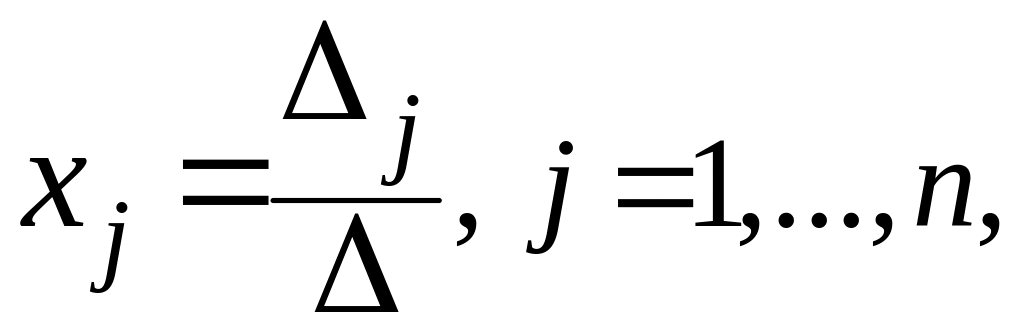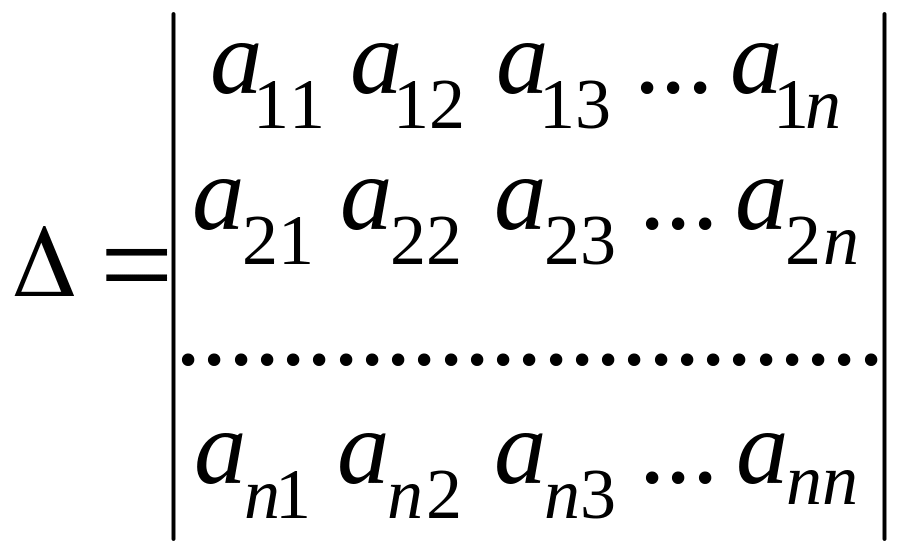Существует правило Крамера решения системы (4), в соответствии с которым где – главный определитель системы, а – также определитель -го порядка, отличающийся от -м столбцом: он заменен столбцом из свободных членов .

Очевидно, что правило Крамера применимо, если , и при исходная система имеет единственное решение. В том случае, если и существует хотя бы один из определителей такой, что , система не имеет решений.

Если и , это означает, что хотя бы одно из уравнений исходной системы является линейной комбинацией других уравнений, и его можно удалить из системы. Остается система из уравнения относительно неизвестных. В ее левой части ищем среди определителей определитель -го порядка отличный от нуля. Берем систему с этим главным определителем, а столбец слагаемых, содержащих переменное , коэффициенты при котором не вошли в этот определитель, переносим в правую часть. Решая новую систему по правилу Крамера, получим решение, зависящее от . Если среди определителей -го порядка нет ненулевых, убираем еще одно уравнение из системы и снова ищем хотя бы один ненулевой определитель, уже -го порядка….

П р и м е р. Решим систему из предыдущего примера методом Крамера. Сначала сосчитаем главный определитель системы: 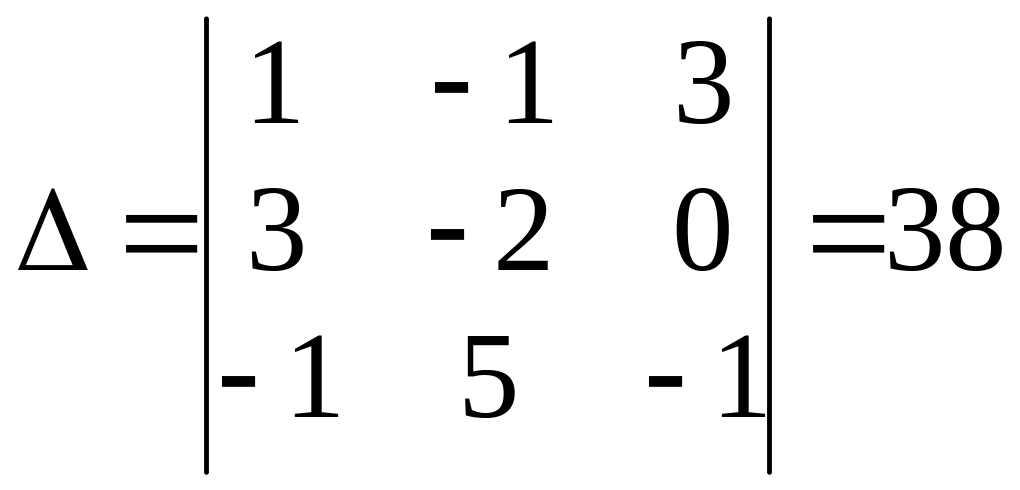. Затем найдем все определители, где столбцы главного определителя заменяются последовательно столбцами свободных членов: .

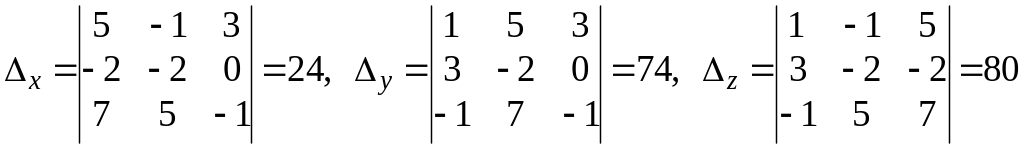В соответствии с формулами Крамера .

Современные пакеты математических программ позволяют решать системы, не прибегая к вычислению определителей. Однако необходимо понимать, почему система, решаемая с помощью компьютера, может не иметь решений или иметь много решений.

Решение систем линейных уравнений в пакете программ MAXIMA проводится следующим образом:

syst.wxm

Построение обратной матрицы для решения систем

Пусть требуется решить систему вида , где – квадратная матрица. Решить – это значит, найти матрицу-столбец . Мы знаем, что в случае решения простейшего алгебраического уравнения достаточно умножить обе части уравнения на , и в случае, когда , мы сразу получим решение: .

Для решения заданной системы в случае, когда , тоже можно найти – матрицу, обратную к матрице ,– и получить решение по формуле .

Для построения обратной матрицы нужно

1. заменить каждый элемент исходной матрицы числом 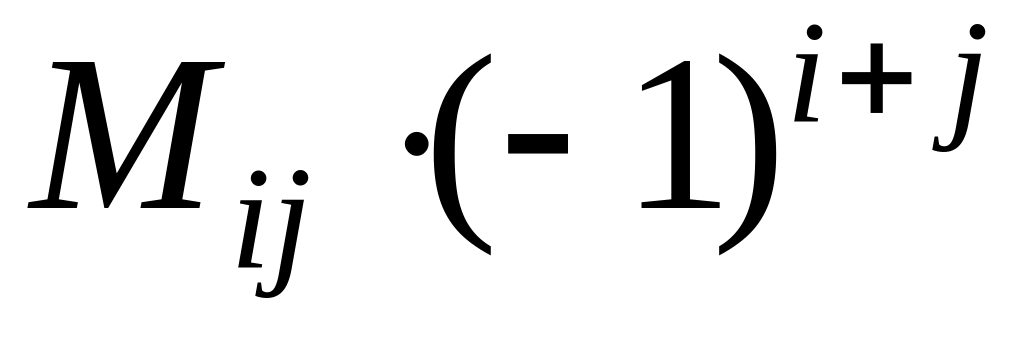, где – минор, соответствующий элементу ,

2. транспонировать полученную на этапе 1) матрицу,

3. умножить полученную на этапе 2) матрицу на 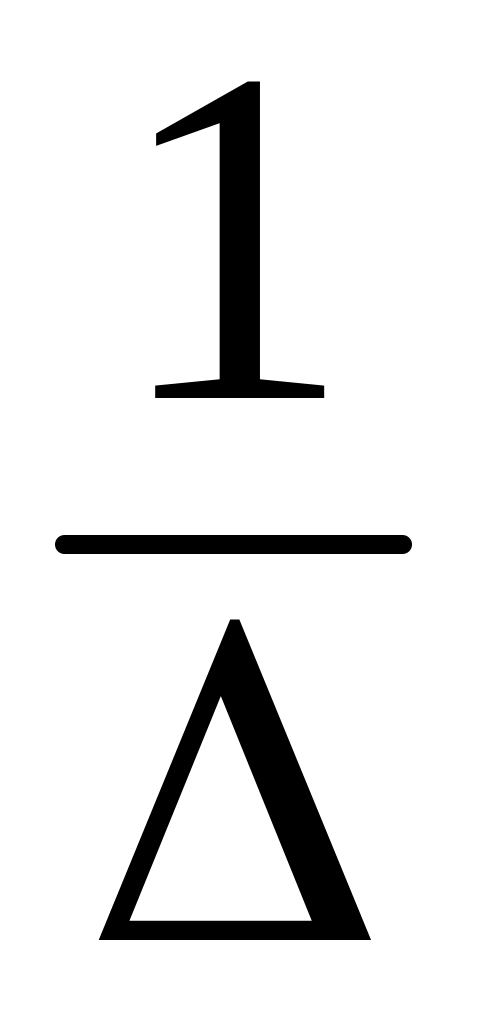, где – определитель исходной матрицы.

Для построения обратной матрицы с помощью пакета программ MAXIMA необходимо использовать команду invert:

matr.wxm