РЯДЫ

Глава 1. Числовые ряды

§1. Основные понятия

Пусть дана бесконечная числовая последовательность: и₁, и₂, и₃,…, и_n,…

Определение. Выражение

и₁ + и₂ + и₃ + … + и_n + … (1)

называется числовым рядом, а элементы последовательности и₁, и₂, и₃,…, и_n,… – членами ряда.

Иногда для обозначения ряда (1) применяют запись : = и₁ + и₂ + и₃ + … + и_n + …

и_n называют общим членом ряда (при произвольном n).

Определение. Сумма n первых членов ряда (1)

(2)

называется n-ой частичной суммой этого ряда.

Очевидно, первая, вторая, третья и т.д. частичные суммы ряда

…

составляют бесконечную последовательность.

Определение. Ряд (1) называется сходящимся, если последовательность частичных сумм S₁, S₂, …, S_n имеет конечный предел

.

Значение этого предела называется суммой ряда.

При этом пишут: или .

Определение. Ряд (1) называется расходящимся, если последовательность его частичных сумм предела не имеет.

§2. Геометрический ряд

Рассмотрим ряд

, (3)

составленный из членов геометрической прогрессии. Часто данный ряд называют геометрическим рядом.

Составим частичную сумму S_n ряда: .

По формуле для суммы n первых членов геометрической прогрессии:

.

Очевидно, что при n изменяется только второе слагаемое последней формулы:

,

причем характер его изменения зависит от того, каково число q.

Геометрический ряд сходится при 1 и расходится при 1 (a0), причем при 1 имеем

.

§3. Простейшие свойства сходящихся рядов

Теорема 1. Если ряд сходится и имеет сумму S, то ряд (где с – некоторая постоянная) также сходится и имеет сумму cS.

Итак, если все члены данного сходящегося ряда умножить на одно и тоже число с, то сходимость этого ряда не нарушится, а сумма его умножится на то же число.

Таким образом, сходящиеся ряды подчиняются, подобно конечным суммам, дистрибутивному закону умножения – в сходящемся ряде можно выносить за скобки общий множитель всех членов ряда.

Теорема 2. Если ряды (1) и (2) сходятся и имеют соответственно суммы S и , то ряды (3) и (4) также сходятся и их суммы соотвественно равны S +  и S – .

Пример. Найдем сумму ряда .

Решение. По теореме 2:

.●

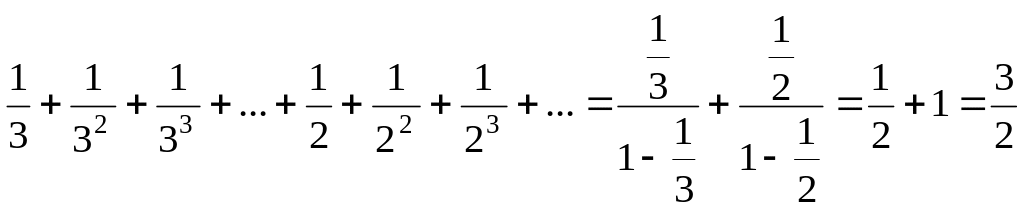Таким образом: 1) сходящиеся ряды можно почленно складывать и вычитать так же, как и конечные суммы; 2) можно умножать члены сходящегося ряда на одно и тоже постоянное число, в результате получаются также сходящиеся ряды.

Замечание 1. Если ряды (1) и (2) оба расходятся, то о рядах (3) и (4) в общем случае ничего сказать нельзя. Они могут оказаться как сходящимися, так и расходящимися.

Рассмотрим два ряда

(5)

и

(6)

Теорема 3. Если сходится данный ряд (5), то сходится и ряд (6),полученный из ряда (5) отбрасыванием конечного числа k его первых членов. Обратно, если сходится ряд (6), то сходится и данный ряд (5).

Теорему 3 можно сформулировать следующим образом:.

На сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

Поэтому для установления сходимости ряда не обязательно учитывать все его члены. достаточно ограничиться членами, «начиная с некоторого места» или «начиная с некоторого номера п».