Зм 1. Предмет математичного програмування.Лінійне програмування

Теоретична частина

1. Графічний метод. В задачах лінійного програмування потрібно

знайти

_n

Z _ext = ∑ c_j x_j j(1,n)

^j=1

при обмеженнях:

_n

1) ∑ a_ij x_j { ≥ = ≤ } b_i i(1,m)

^j=1

2) x_j ≥ 0.

При кількості невідомих n = 2, або для n > 2, якщо при зведенні системи нерівностей до системи рівнянь шляхом введення додаткових змінних кількість змінних n на 2 більша числа обмежень m, тобто n – m = 2, задача розв'язується графічним методом за таким алгоритмом:

1. В системі координат Х₁ОХ₂ (перший квадрант системи координат двомірного простору, що обумовлено умовою невід'ємності змінних) представимо обмеження-нерівності а_і1х₁ + а_і2х₂ { ≥} b, кожне з яких поділяє систему координат на дві напівплощини, межами яких є прямі, визначені рівняннями

а_і1х₁ + а_і2х₂ = b.

2. Для того, щоб визначити, для якої напівплощини виконується обмеження, потрібно взяти координати точок в першій і другій напівплощинах і перевірити, в якій із напівплощин виконується обмеження-нерівність.

3. Напівплощини, в яких виконуються обмеження, при перетині в системі координат Х₁ОХ₂ утворюють спільну частину, яка називається багатокутником розв'язків. Кожна точка цього багатокутника є розв'язком задачі, тому що в ній виконуються всі обмеження. Такий розв'язок називається допустимим.

4. Будуємо вектор N з координатами точок О (0,0) та N (с₁, с₂), який задає напрям зміни значення цільової функції (для задач максимізації в напрямку вектору, для задач мінімізації - в протилежному).

5. Будуємо пряму с₁ + с₂ =const, перпендикулярну до вектора N, яка характеризує цільову функцію.

6. Пересуваємо пряму с₁ + с₂ = const паралельно саму до себе до тих пір, поки вона не торкнеться крайньої точки (вершини) багатокутника допустимих розв'язків. В цій точці цільова функція досягає екстремального значення. При розв"язанні задачі на максимум цільової функції екстремальна точка знаходиться якнайдалі від початку координат, а на мінімум – якнайближче.

7. Визначаємо координати точки, в якій цільова функція досягає екстремального значення, для чого розв'язуємо систему рівнянь двох прямих, перетином яких є оптимальна точка. Отримані координати точки є оптимальним розв'язком задачі.

8. Обчислюємо значення цільової функції і перевіряємо виконання обмежень.

1.2. Симплексний метод. Симплексний метод є універсальним методом розв'язування задач лінійного програмування, в основу алгоритму якого покладена ідея цілеспрямованого перегляду вершин n-мірного опуклого багатокутника допустимих розв’язків. Обстеження вершин багатокутника допустимих розв’язків можна почати після визначення будь-якої однієї з них, тобто спочатку потрібно отримати початковий опорний розв’язок задачі. Тому весь алгоритм симплексного методу поділяють на два етапи:

1) знаходження початкового опорного розв’язку (плану) задачі - задачу приводять до канонічної форми шляхом введення в кожне обмеження-нерівність по одній додатковій змінній (при обмеженнях виду менше або дорівнює (≤) із знаком "+", а при обмеженнях виду більше або дорівнює (≥) із знаком "-" ). Прийнявши в якості базисних невід’ємні додаткові змінні, отримуємо початковий опорний розв’язок задачі;

2) знаходження оптимального розв’язку (плану) задачі – виконується цілеспрямований перегляд базисних розв’язків, починаючи з опорного, так щоб забезпечувалося монотонне збільшення (для задач максимізації) або зменшення (для задач мінімізації) значення цільової функції. Для цього на кожній ітерації (етапі) розрахунків до базисного розв’язку вводиться одна невідома та відповідно одна невідома виводиться. Розрахунки виконуються в симплексних таблицях за методом виключень Жордана-Гаусса доти, поки не буде отримано оптимальний розв’язок.

При розв’язанні задач в симплексних таблицях алгоритм симплексного методу складається із таких кроків:

1. Знаходження розв’язуючого стовпчика симплексної таблиці (невідома цього стовпчика вводиться в новий базисний розв’язок) – для цього в рядку цільової функції знаходимо максимальний за модулем коефіцієнт і відповідний йому стовпчик вважаємо розв’язуючим.

2. Знаходження розв’язуючого рядка симплексної таблиці (невідома цього рядка виводиться із нового базисного розв’язку) – для цього визначаємо найменшу частку від ділення значень базисних невідомих на додатні коефіцієнти розв'язуючого стовпчика і відповідний їй рядок вважаємо розв’язуючим.

3. Коефіцієнт, що знаходиться на перетині розв’язуючих стовпчика і рядка, називається розв’язуючим.

4. Перехід до нової симплексної таблиці здійснюється за такими правилами:

а) розраховуються коефіцієнти рядка невідомої, яка вводиться в новий базисний розв’язок – для цього коефіцієнти розв’язуючого рядка попередньої симплексної таблиці діляться на розв’язуючий коефіцієнт;

б) для знаходження коефіцієнтів інших рядків і коефіцієнтів цільової функції нової симплексної таблиці потрібно від коефіцієнтів відповідного рядка (цільової функції) попередньої симплексної таблиці відняти добутки коефіцієнтів отриманого нового рядка (п. 4а) на відповідний коефіцієнт розв’язуючого стовпчика попередньої симплексної таблиці.

Умова оптимальності розв'язання задачі:

1. Для задач максимізації цільової функції розв'язок задачі буде оптимальним, якщо в рядку цільової функції Z_max всі коефіцієнти мають додатні значення або дорівнюють нулю.

2. Для задач мінімізації цільової функції розв'язок задачі буде оптимальним, якщо в рядку цільової функції W_min всі коефіцієнти мають від'ємні значення або дорівнюють нулю.

Розрахунки повторюються на кожній ітерації до отримання оптимального розв’язку.

Зауваження 1. Якщо розв'язуючий стовпчик має тільки від'ємні коефіцієнти і не можна знайти розв'язуючий рядок, то цільова функція не обмежена зверху (при знаходженні максимуму цільової функції) або знизу (при знаходженні мінімуму цільової функції) на множині допустимих розв'язків. Задача не має оптимального розв"язку. Треба змінити умови задачі.

Зауваження 2. Якщо при визначенні розв'язуючого стовпчика в Z - рядку коефіцієнти мають однакові значення, то вибирається один будь-який з них.

Зауваження 3. Якщо при визначенні розв'язуючого рядка є однакові симплексні відношення, то вибирається одне будь-яке з них.

1.3. М-задача. В задачах з обмеженнями тільки менше або дорівнює (≤ ) початковий план завжди містить одиничну підматрицю (Е_m), що є ознакою отримання опорного плану задачі. Проте на практиці, як правило, найбільш поширеними є задачі з обмеженнями виду як менше або дорівнює (≤ ), так і більше або дорівнює (≥). Для отримання канонічної форми задачі додаткові невідомі в обмеженнях виду більше або дорівнює (≥) вводяться зі знаком мінус, і тому не можуть входити до базисних (порушується правило невід'ємності базисних невідомих). В цьому випадку для отримання опорного плану задачі застосовують метод штучної бази. Ідея методу полягає в тому, що до лівої частини кожного обмеження-рівняння, яке задане в канонічній формі і яке не має одиничного базису (Е_m), додають по одній додатній штучній змінній, утворюючи таким чином штучний базис. Але базисний розв'язок, який містить хоча б одну штучну невідому, є недопустимим. Для отримання допустимого опорного плану задачі всі штучні невідомі потрібно вивести із базисного розв'язку. Для цього штучні невідомі вводяться в цільову функцію з великим (наприклад, більшим від усіх коефіцієнтів задачі) модулем М (для задач максимізації цільової функції із знаком мінус, а для задач мінімізації із знаком плюс). Отриману задачу називають М-задачею.

Розв'язання М-задачі також поділяють на два етапи:

1) знаходження допустимого базисного розв'язку - досягається виведенням із початкового розв'язку всіх штучних невідомих. Для цього із коефіцієнтів при М утворюють додатковий рядок цільової функції F_min і задачу розв'язують на мінімум цієї функції. Допустимий базисний розв'язок отримують тоді, коли всі штучні невідомі виведені із базису, а значення додаткової цільової функції F_min дорівнює нулю;

2) знаходження оптимального розв'язку - якщо отримано допустимий базисний розв'язок, то розрахунки продовжуються за алгоритмом симплексного методу на екстремум основної цільової функції до отримання оптимального розв'язку.

Зауваження 1. Якщо при розв'язанні М-задачі F_min=0, а в базисному розв’язку є штучні зміні, то задача не має допустимого розв’язку. В цьому випадку умови задачі суперечливі і їх треба змінити.

Графічний мето . Приклад 1.1. Для виробництва зерна озимої пшениці та кукурудзи виділено 600 га ріллі та 32000 люд.-год.. Затрати праці та урожайність (в розрахунку на 1 га) такі:

Показник	Пшениця	Кукурудза
1. Затрати праці, люд.-год.	40	80
2. Урожайність, ц	50	70

Посівна площа кукурудзи повинна бути не менша 100 га. Знайти посівні площі озимої пшениці та кукурудзи, які б забезпечили максимум виробництва зерна.

Розв'язання. Для побудови економіко-математичної моделі і введемо позначення:

х₁ – посівна площа озимої пшениці, га

х₂ – посівна площа кукурудзи на зерно, га

Z – обсяг виробництва зерна, ц.

Тоді, умови задачі в математичній формі можна записати так:

1. Умова використання ріллі: посівні площі озимої пшениці та кукурудзи не повинні перевищувати наявної площі ріллі: х₁ + х₂ 600

2. Умова використання трудових ресурсів: затрати праці на вирощування сільськогосподарських культур не повинні перевищувати наявного обсягу трудових ресурсів: 40х₁ + 80х₂ 32000

3. Умова обмеження площі кукурудзи: посівна площа кукурудзи на зерно повинна бути не менше 100 га: х₂ 100

4. Умова невід'ємності змінних: посівні площі сільськогосподарських культур не можуть бути від'ємними числами: х₁ 0; х₂ 0.

Кінцеву мету задачі – отримання максимуму зерна - запишемо як функцію двох змінних х₁ і х₂: Z_mаx= 50х₁ + 70х₂

Нерівності на графіку являють собою напівплощини, межами яких є прямі лінії, визначені рівняннями відповідно: х₁+х₂ = 600 (L₁); 40х₁+80х₂ = 32000 (L₂) та х₂ = 100 (L₃). Побудуємо ці прямі в додатному квадранті системі координат Х₁ОХ₂, оскільки х₁ 0; х₂ 0. Для побудови на графіку будь-якої прямої знайдемо принаймні дві точки, які їй належать, наприклад, для рівняння х₁ + х₂ =600: якщо х₁ = 0, то х₂ = 600, а якщо х₂ = 0, то х₁ = 600.Через точки (0;600) та (600;0) проведемо пряму L₁. Аналогічно побудуємо прямі L₂ та L₃ (рис.1.)

Оптимальний розв'язок знаходимо, визначаючи напрямок зростання цільової функції

Z_max= 50x₁ + 70x₂

Для цього побудуємо вектор N з координатами точок О (0;0) - початок координат - та N (50;70) - оцінки невідомих цільової функції. В точці О проведемо до вектора N перпендикуляр, який відповідає прямій рівня цільової функції Z=0.

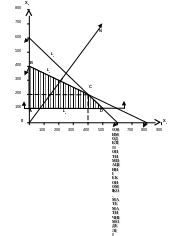
Z

Рис1. Графічний метод розв"язання задач лінійного програмування

Значення Z зростає в напрямку вектора N (див. рис. 1), тому пряму Z=0 пересуваємо паралельно саму до себе в напрямку вектора N доти, поки вона не торкнеться крайньої верхньої точки (вершини) багатокутника допустимих розв'язків АВСD. Оптимальним розв"язком задачі будуть координати точки С, яка одночасно належить багатокутнику допустимих розв'язків АВСD і прямій рівня цільової функції Z_max =50х₁+70х₂, а також знаходиться якнайдалі від початку координат (задач розв"язується на максимум цільової функції). На рис.2 видно, що точка С є точкою перетину прямих L₁ і L₂. Отже, щоб визначити х₁ і х₂, потрібно розв'язати систему рівнянь:

х₁+х₂=600

40х₁+80х₂=32000

Розв'язок системи рівнянь: х₁=400; х₂=200.

Висновки. Для отримання максимальної кількості зерна в обсязі 34000 ц

(Z_max =50400+70200=34000) площа озимої пшениці повинна дорівнювати 400 га, (х₁=400), а кукурудзи – 200 га (х₂=200).. При цьому повністю використані площа ріллі (400+200=600) та трудові ресурси (40400+80200=32000). Площа кукурудзи перевищує задану на 100 га (200-100=100).

Задачі для самостійного розв'язування

Задача 1.1. В господарстві для вирощування кукурудзи на зерно та ячменю виділено 400 га ріллі та 12000 люд.-год.. Затрати праці на 1 га та урожайність сільськогосподарських культур наведені в таблиці.

Знайти посівні площі сільськогосподарських культур з метою отримання максимальної кількості фуражного зерна, якщо відомо, що площа кукурудзи на зерно повинна бути не менше 50 га.

Сільськогосподарська культура	Варіант *)	Затрати праці на 1 га, люд.-год.	Урожайність, ц з 1га
Кукурудза на зерно	0	60	60
	1	50	55
	2	40	50
	3	60	60
	4	50	35
	5	40	50
	6	60	60
	7	50	55
	8	40	50
	9	60	60
Ячмінь	0	30	30
	1	25	40
	2	20	30
	3	30	55
	4	25	45
	5	20	35
	6	30	40
	7	25	35
	8	20	30
	9	30	40

^*) Варіант технології вирощування кукурудзи на зерно вибирається за передостанньою цифрою шифру Р, а ячменю – за кінцевою К.

Симплексний метод. Приклад 1.2. В господарстві для вирощування кукурудзи на зерно та ячменю виділено 400 га ріллі, 18000 люд.-год. та 1800 ц мінеральних добрив. Вихід концентрованих кормів та затрати ресурсів (в розрахунку на 1 га) наведені нижче:

Показник	Кукурудза на зерно	Ячмінь
1. Затрати праці, люд.-год.	50	30
2. Внесення мінеральних добрив, ц	6	3
3. Вихід кормів, ц к. од	90	50

Знайти посівні площі зернофуражних культур для отримання максимальної кількості фуражного зерна.

Розв'язання. Для формулювання економіко-математичної моделі задачі введемо позначення:

х₁ - площа кукурудзи на зерно, га

х₂ - площа ячменю, га

Z - обсяг виробництва концентрованих кормів, ц к. од.

Тоді умови задачі в математичній формі можна записати так:

1. Умова використання ріллі: х₁ + х₂ ≤ 400

2. Умова використання трудових ресурсів: 50х₁ + 30х₂ ≤ 18000

3. Умова використання мінеральних добрив: 6х₁ + 3х₂ ≤ 1800

4. Умова невід"ємності змінних: х₁ 0, х₂ 0

Критерій оптимальності – виробництво максимальної кількості концентрованих кормів -

Z_max = 90х₁ + 50х₂

Запишемо задачу в канонічній формі, шляхом введення до лівої частини

кожної нерівності по одній невід'ємній додатковій змінній, які в умовах даної задачі мають такий економічний зміст:

S₁ - кількість невикористаної площі ріллі, га;

S₂ - кількість невикористаних трудових ресурсів, люд.-год.;

S₃ - кількість невикористаних мінеральних добрив, ц.

В цільову функцію Z_max додаткові змінні вводяться з нульовою оцінкою. Тоді,

Z_max = 0 - ( - 90 х₁ - 50 х₂)

х₁ + х₂ + S₁ = 400

50 х₁ + 30 х₂+ S₂ = 18000

6 х₁ + 3 х₂ + S₃ = 1800

х₁ ≥ 0, х₂ ≥ 0; S₁ ≥ 0; S₂ ≥ 0; S₃ ≥ 0;

Прийнявши в якості базисних додаткові змінні, отримуємо допустимий базисний розв'язок задачі: х₁ = х₂ = 0; S₁ = 400; S₂ = 18000; S₃ = 1800 та Z_max = 0.

Розв'язання задачі виконаємо в симплексних таблицях, записавши в першу симплексну таблицю 1.2.1 допустимий базисний розв'язок.

Симплексна таблиця 1.2.1

Базисні змінні	Значення базисних змінних	х1	х2	S1	S2	S3	L
S1	400	1	1	1	0	0	400
S2	18000	50	30	0	1	0	360
S3	1800	6	3	0	0	1	300
max	0	-90	-50	0	0	0

В симплексній таблиці 2.1.1 небазисні змінні х₁ та х₂ в Z - рядку мають від'ємні коефіцієнти (відповідно -90 та -50), тому розв'язок задачі не оптимальний.

Небазисною змінною, яка буде введена в базис буде змінна х₁ (-90). Для того, щоб в новий розв'язок ввести цю змінну потрібно з розв'язку вивести одну з базисних змінних (S₁, S₂ або S₃). Для цього визначимо

_{min {400 / 1= 400; 18000 / 50 = 360 ; 1800 / 6 = 300 } = 300}

Змінною, яка буде виведена із базисного розв'язку, буде та, для якої розраховане відношення буде мінімальним. В симплексній таблиці 1.2.1 мінімальне відношення (300) належить 3-му рядку, якому відповідає змінна S₃. Розв'язуючий елемент дорівнює 6.

Пошук нового базисного розв'язку виконаємо за допомогою методу виключень Жордана – Гауса:

1. 3-й рядок: (1800630 01) / 6 = ( 30010,5000,167)

2. Розрахунки коефіцієнтів всіх інших рівнянь (рядків), включаючи і Z-рівняння, нової симплексної таблиці виконуються за схемою: відповідний рядок нової симплексної таблиці = відповідний рядок попередньої симплексної таблиці - (новий розв'язуючий рядок)  (відповідний коефіцієнт розв'язуючого стовпчика попередньої симплексної таблиці):

1-й рядок
(400		1		1		1		0		0)-
-(300		1		0,5		0		0		0,167)1
= (100		0		0,5		1		0		-0,167)
2-й рядок
(18000		50		30		0		1		0 ) -
-(300		1		0,5		0		0		0,167)50
= (3000		0		5		0		1		- 8,333)
Z рядок
(0	-90		-50		0		0		0) -
-(300	1		0,5		0		0		0,167)(-90)
= (27000	0		-5		0		0		15)

Нова симплексна таблиця 1.2.2 має такий вигляд (зазначимо, що в базисний розв'язок замість змінної S₃ введена змінна х₁).

Симплексна таблиця 1.2.2

Базисні змінні	Значення базисних змінних	х1	х2	s1	s2	s3	L
S1	100	0	0,5	1	0	-0,167	200
S2	3000	0	5	0	1	-8,333	600
Х1	300	1	0,5	0	0	0,167	600
Zmax	27000	0	-5	0	0	15

В симплексній таблиці 1.22 одержано новий базисний розв'язок: Z_max = 27000; Х₁ = 300; Х₂ = 0; S₁ = 100; S₂ = 3000; S₃ = 0. В зв'язку з тим, що небазисна змінна х₂ в Z-рядку має від'ємний коефіцієнт (-5), базисний розв'язок в симплексній таблиці

2.1.2 не оптимальний. Продовжимо розв'язання задачі. В симплексній таблиці 1.2.2 колонка "х₂" є розв'язуючою. Визначимо симплексні відношення:

_{min{100 / 0.5 = 200; 3000 / 5 = 600; 300 / 0,5 = 600} = 200}

Мінімальне відношення (200) належить 1-му рядку, тому до нового базисного розв'язку замість S₁ вводимо х₂. Розв'язуючим елементом симплексної таблиці 1.2.2 буде 0,5. Пошук нового базисного розв'язку здійснюємо знову за допомогою обчислювальних операцій методу Жордана-Гаусса:

1 -й рядок - (10000,51 0- 0,167) / 0,5 = (2000120- 0,333)

2-й рядок
(3000	0	5	0	1	-8,333)-
- (200	0	1	2	0	-0,333)5
= (2000	0	0	-10	1	-6,667)
3-й рядок
(300	1	0.5	0	0	0,167) -
-(200	0	1	2	0	-0,3330,5
= (200	1	0	-1	0	0,333)
Z рядок
(27000	0	-5	0	0	15) -
-(200	0	1	2	0	-0,3330.5
= (28000	0	0	10	0	13,333)

Запишемо симплексну таблицю 1.2.3.

Симплексна таблиця 1.2.3

Базисні змінні	Значення базисних змінних	Х1	Х2	S1	S2	S3
Х2	200	0	1	2	0	-0,333
S2	2000	0	0	-10	1	-6,667
Х1	200	1	0	-1	0	0,333
Zmax	28000	0	0	10	0	13,333

В симплексній таблиці 1.2.3 в Z_max-рядку відсутні від'ємні елементи, тому отриманий базисний розв'язок є оптимальним: Z = 28000; х₁ = 200; х₂ = 200;

S₁ = 0;S₂ = 2000; S₃ = 0.

Висновки. Для виробництва максимальної кількості концентрованих кормів в обсязі 28000 ц к.од. (Z_max=28000) в господарстві потрібно вирощувати 200 га (х₁=200) кукурудзи на зерно та 200 га (х₂=200) ячменю. Площа ріллі та мінеральні добрива використовуються повністю (S₁=0; S₃=0), а невикористані трудові ресурси дорівнюють 2000 люд.-год. (S₂=2000).

Задачі для самостійного розв'язання

Задача 1.2. Для вирощування озимої пшениці, кукурудзи на зерно та ячменю виділено 400 га ріллі, 24000 люд.-год.. трудових ресурсів та 1600 ц мінеральних добрив. Урожайність, затрати праці та мінеральних добрив (в розрахунку на 1 га) наведені в таблиці.

Визначити посівні площі сільськогосподарських культур з метою максимального виробництва зерна.

Сільськогосподар- ська культура	Варіант *)	Затрати праці , люд.-год.	Внесення мінеральних добрив, ц	Урожайність, ц
Озима пшениця	Для всіх варіантів	40	5	50
Кукурудза на зерно	0	40	4	40
	1	50	5	50
	2	60	8	64
	3	75	10	80
	4	80	4	60
	5	40	5	45
	6	50	8	59
	7	60	10	70
	8	75	4	55
	9	80	5	65
Ячмінь	0	20	2	28
	1	24	2,5	31
	2	25	4	36
	3	30	2	33
	4	32	2.5	35
	5	20	4	33
	6	24	2	30
	7	25	2,5	32
	8	30	4	38
	9	32	2	34

*) Варіант технології вирощування кукурудзи на зерно вибирається за передостанньою цифрою шифру Р, а варіант технології вирощування ячменю - за кінцевою цифрою шифру К.