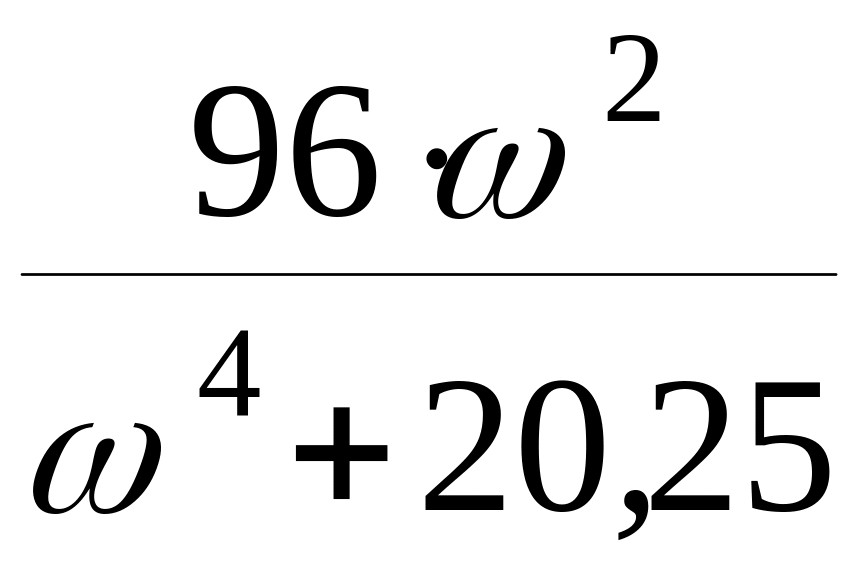Задание 1

Условие:

Случайный стационарный эргодический центрированный нормальный сигнал X(t) задан своим энергетическим спектром S_X(ω).

Требуется:

1. найти корреляционную функцию сигнала R_X(τ), определить дисперсию сигнала σ_X² и стандартное отклонение σ_X, построить график корреляционной функции и объяснить характер ее изменения при изменении параметров энергетического спектра сигнала;

2. найти вероятность того, что реализация случайного сигнала через промежуток времени t₀ после прохождения через нуль примет значение, большее σ_X;

3. определить шаг дискретизации h, достаточный для восстановления дискретизированного сигнала X(ih) c помощью двух первых полиномов Лежандра (линейная аппроксимация) с собственной средней квадратической погрешностью, не превышающей 1% от стандартного отклонения сигнала X(t);

4. найти значение коэффициента корреляции между сечениями сигнала, разделенными шагом дискретизации.

Исходные данные (вариант 18):

Энергетический спектр сигнала Х(t) - .

Варианты задания №1

№№			№№
1	2	3	4	5	6
1		0,01 с	7		2,0 с
2		5 мс	8		10 мс
3		2,5 с	9		0,35 c
4		70 мс	10		0,7 mc
5		3 с	11		1,2 mc
6		0,15 с	12		10 mc
13		7 c	20		20 mc
14		0,5 mc	21		3,5 c
15		6 c	22		7 mc
16		0,4 mc	23		8 mc
17		0,2 c	24		0,1 c
18		1 c	25		7 mc
19		2 c	26		0,5 c
27		0,35 c	31		0,1 c
28		0,24 c	32		4,5 mc
29		20 c	33		0,08 c
30		14 mc	34		6 mc

Решение:

1. Нахождение корреляционной функции сигнала R_X(τ), определение дисперсии сигнала σ_X² и стандартного отклонения σ_X, построение графика корреляционной функции и объяснение характера ее изменения при изменении параметров энергетического спектра сигнала.

Задан случайный стационарный эргодический центрированный нормальный сигнал X(t).

Случайной называется такая функция, которая может принять тот или иной конкретный вид, неизвестно заранее какой именно. Этот вид называется реализацией. В данном случае случайная функция зависит от времени.

Под стационарным понимается такой случайный процесс, n – мерная плотность распределения вероятности которого не меняется при любом сдвиге всей группы точек вдоль оси времени.

Стационарный случайный процесс называется эргодическим, если любая его реализация имеет одни и те же статистические свойства. Следовательно, для эргодических случайных процессов любая статистическая характеристика, получаемая усреднением по множеству реализаций, может быть получена также усреднением за достаточно большой промежуток времени по одной реализации случайного процесса. Т.о. свойство эргодичности позволяет рассматривать не множество, а всего одну реализацию.

Случайная величина X(t) подчинена нормальному закону распределения, если плотность вероятности ее имеет вид

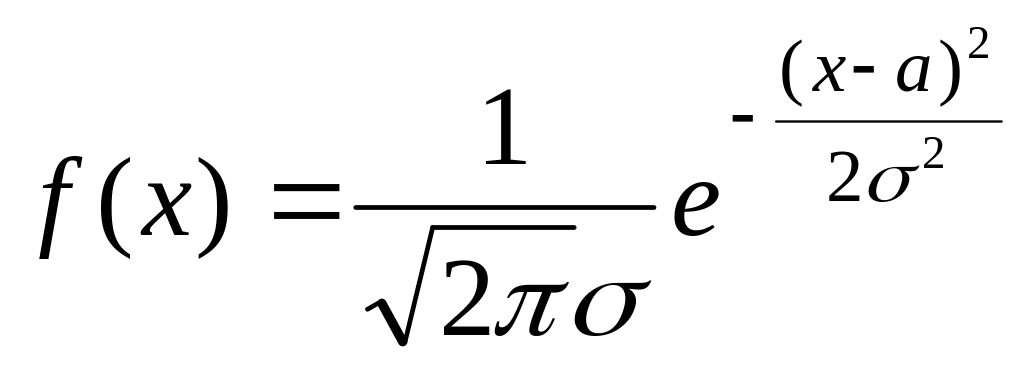, (1.1)

где а – математическое ожидание X(t)

σ – стандартное отклонение X(t), σ>0.

Если X(t) центрированная величина, то а=0 и плотность распределения вероятности ее будет иметь вид

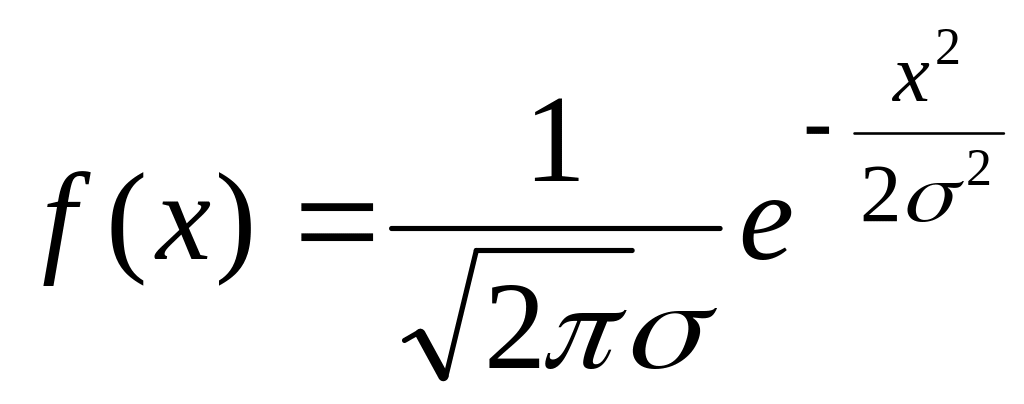(1.2)

Функция распределения X(t) имеет следующий вид

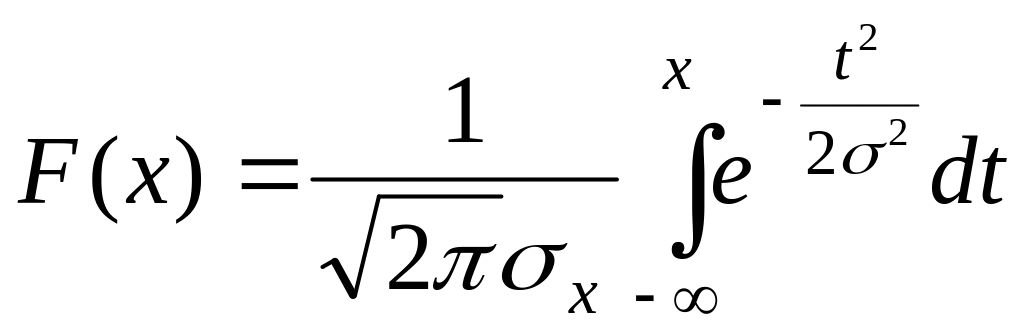(1.3)

Одномерная плотность вероятности и связанные с ней числовые характеристики позволяют получить важную информацию о свойствах случайного процесса. Однако для решения многих задач таких сведений не достаточно, так как они дают вероятностное представление о случайном процессе X(t) только в отдельные моменты времени и не определяют его изменение во времени. Для описания временных характеристик случайного процесса необходимо использовать корреляционную функцию и спектральных характеристики случайного процесса.

Начальный корреляционный момент двух значений случайной функции X(t) и X(t₁), взятых в моменты времени t и t₁ носит название корреляционной функции. Т.е. корреляцононная функция показывает степень сходства между сигналом и его сдвинутой копией.

В случае стационарности процесса корреляционная функция не будет зависеть от текущего значения времени t, и будет определяться только временным сдвигом . С учетом эргодичности стационарного процесса корреляционной функцией можно назвать среднее по времени от произведения X(t) и X(t+τ)

(1.4)

Для стационарного процесса корреляционная функция определяет зависимость случайной величины x в последующий момент времени (t+ τ) от предшествующего значения в момент t.

Корреляционная функция стационарного процесса является четной функцией. При τ=0 значение корреляционной функции является ее наибольшим значением. Значение корреляционной функции чаще всего будет тем меньше, чем больше промежутки времени τ , так как связь между далеко отстоящими друг от друга значениями х будет обычно слабее. Чем менее инерционен (более подвижен) объект наблюдения, тем быстрее убывает R(τ) c увеличение τ.

Задан энергетический спектр сигнала Х(t) (рис.1) - Он также носит название спектральной плотности сигнала и является четной функцией своего аргумента. Обладает важным свойством: интегрирование спектральной плотности по всем частотам от дает средний квадрат исходной функции времени Х(t). По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от ω до ω+dω.

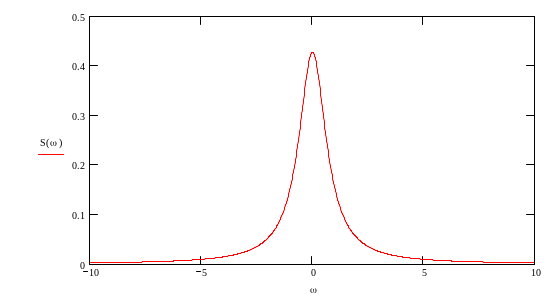
Рисунок 1 Энергетический спектр сигнала X(t)

Спектральная плотность и корреляционная функция случайных процессов представляют собой взаимные преобразования Фурье, т.е. они связаны интегральными зависимостями. Т.к. спектральная плотность и корреляционная функция представляют собой четные вещественные функции, то их можно представить следующими соотношениями

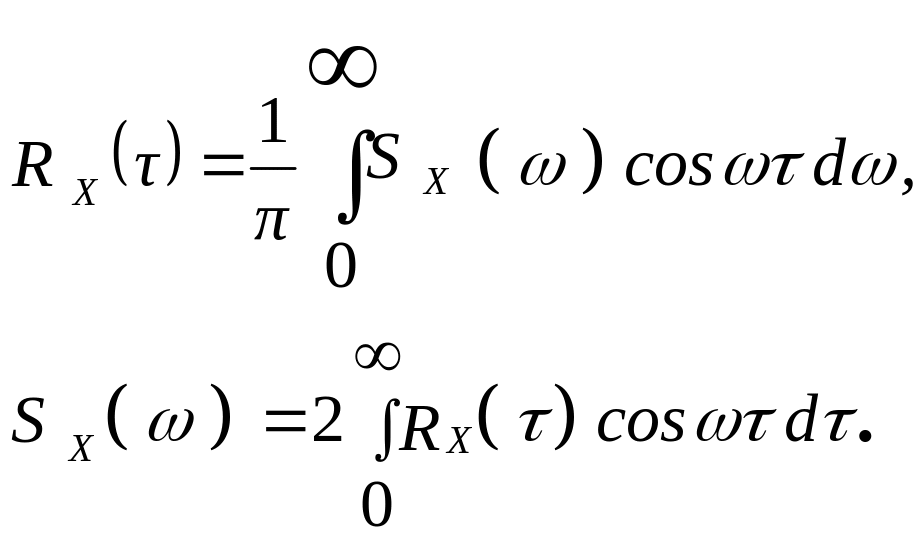(1.5)

Результаты интегрирования для наиболее распространенных случаев приведены в специальных таблицах, из которой имеем

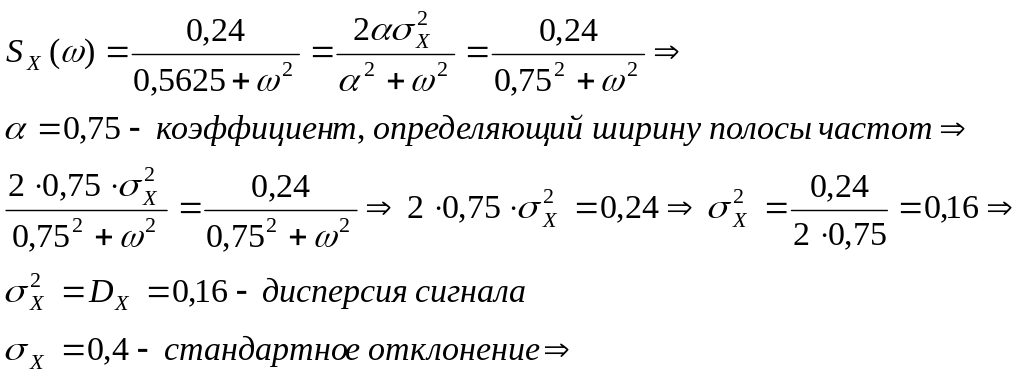
Корреляционная функция (в соответствии с таблицей для определенного вида энергетического спектра)

Таким образом, график корреляционной функции имеет следующий вид

Рисунок 2 График корреляционной функции

Рассмотрим характер изменения корреляционной функции сигнала при изменении параметров энергетического спектра, а именно, коэффициента, определяющего ширину полосы частот, и стандартного отклонения по сравнению с полученной функцией. Наглядный результат представлении ниже на рисунках 3 и 4.

- полученная функция

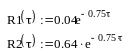- функции с измененным стандартным отклонением

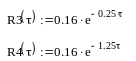- функции с измененным коэффициентом, определяющим ширину полосы частот

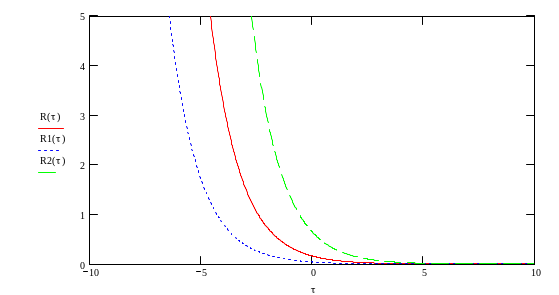
Рисунок 3 Изменение стандартного отклонения

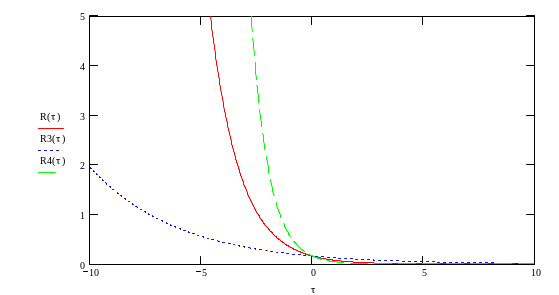
Рисунок 4 Изменение коэффициента, определяющего ширину полосы частот

Связь между спектральной плотностью и видом функции времени Х(t) заключается том, что чем «уже» график спектральной плотности, т.е. чем меньшие частоты представлены в спектральной плотности, тем медленнее изменяется величина Х во времени. Связь между видом спектральной плотности и видом функции времени получается обратной по сравнению со связью между корреляционной функцией и самим процессом (чем менее инерционен (более подвижен) объект наблюдения, тем быстрее убывает R(τ) c увеличение τ). Отсюда вытекает, что более «узкому» графику спектральной плотности соответствует более «широкий» график корреляционной функции и наоборот.

2. Нахождение вероятности того, что реализация случайного сигнала через промежуток времени t₀ после прохождения через нуль примет значение, большее σ_X .

Как уже было сказано ранее, случайной называется такая функция, которая может принять тот или иной конкретный вид, неизвестно заранее какой именно. Этот вид называется реализацией. В практике анализа случайных сигналов применение операции сдвига во времени позволяет получить два сечения случайного процесса в произвольные моменты времени, а именно, в нашем случае имеем два сечения случайного сигнала X(t) в моменты времени , где .

Совокупность этих двух сечений образуют двумерную случайную величину , которая описывается двумерной плотностью вероятности (совместной плотностью распределения значений сигнала X(t)) , которая имеет следующий вид

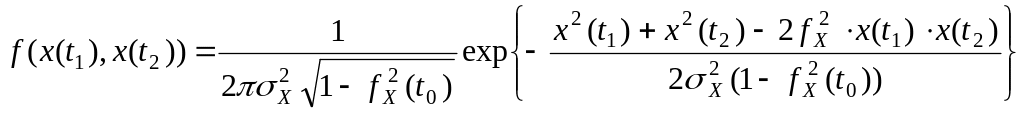, (1.6)

Где ,

- значение нормированной корреляционной функции R_X(τ) при τ=t₀ .

Условная плотность распределения значений сигнала X(t) в момент при условии, что в сечении t₁ сигнал имел значение , находится из следующего выражения

(1.7)

где - плотность распределения вероятности значений сигнала X(t) в первом сечении, находится в соответствии с нормальным законом распределения по формуле (1.2)

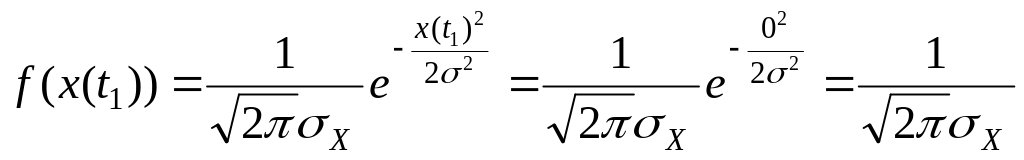(1.8)

Найдем условную плотность распределения значений сигнала X(t) в момент . Для этого в выражение (1.7) подставим выражения (1.6) и (1.8)

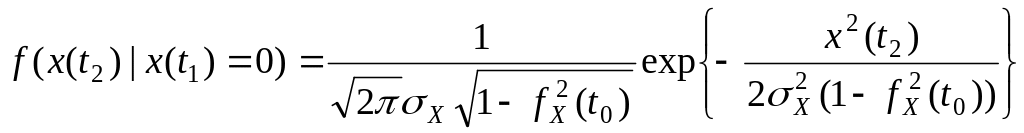(1.9)

Далее необходимо найти вероятность того, что реализация случайного сигнала через промежуток времени t₀ после прохождения через нуль примет значение, большее σ_X. Для этого воспользуемся связью интегральной функции распределения F(x) (формула (1.3)) с функцией Лапласа Ф (функция верхнего предела, значения которой табулированы) для нормального распределения

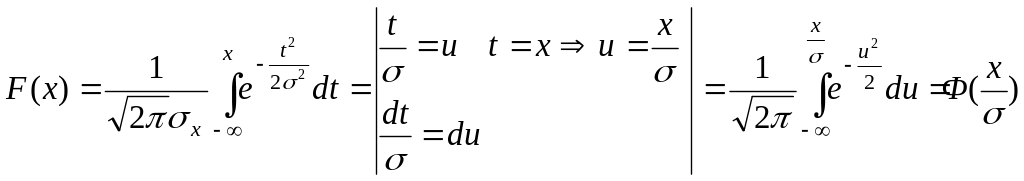(1.10)

Т.к. , то, пользуясь выражением (1.10) и найденной условной плотностью распределения (1.9), найдем искомую вероятность

Таким образом, вероятность того, что реализация случайного сигнала через промежуток времени t₀ после прохождения через нуль примет значение, большее σ_X, равна

.

3. Определение шага дискретизации h, достаточного для восстановления дискретизированного сигнала X(ih) c помощью двух первых полиномов Лежандра (линейная аппроксимация) с собственной средней квадратической погрешностью, не превышающей 1% от стандартного отклонения сигнала X(t).

Наиболее известными специальными функциями, широко используемыми при разложении непрерывного сигнала в обобщенный ряд Фурье, являются полиномы Лежандра, которые имеют вид

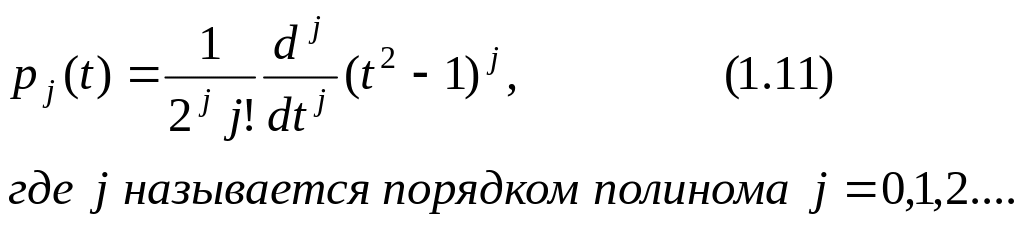
По условию, для восстановления дискретизированного сигнала X(ih) необходимо воспользоваться двумя первыми полиномами Лежандра

(1.12)

Полномы Лежандра ортонормированны на интервале [-1;1] с весом ρ(t)=1. Модель экспериментального процесса X(t), построенная как ряд Фурье по полиномам Лежандра, имеет вид

(1.13)

Коэффициенты Фурье-Лежандра вычисляют по формуле:

(1.14)

Модель в виде ряда Фурье по ортогональным функциям для экспериментальной функции X(t) должна строиться на интервале ортонормированности базисных функций. Это значит, что если экспериментальная реализация X(t) определена на интервал [0,T], то чтобы построить ее модель в виде ряда Фурье по полиномам Лежандра нужно перейти от этого интервала к интервалу [-1;1] путем замены переменных:

(1.15)

Ряд Фурье – Лежандра примет вид:

(1.16)

Коэффициенты Фурье-Лежандра вычисляют по формуле:

(1.17)

Часто экспериментальная реализация представляет собой множество дискретных значений , снимаемых в течении определенного интервала времени Т, в точках , где i – номер отсчета, i=0,1,…N.

N – количество отсчетов или длина реализации, h – интервал между соседними отсчетами или шаг дискретизации, который вычисляется по формуле

(1.18)

где Т – длительность интервала наблюдения.

Для такого дискретизированного сигнала:

(1.19)

Тогда ряд Фурье – Лежандра также представляет собой набор дискретных значений, каждое из которых можно получить по формуле

(1.20)

Коэффициенты Фурье-Лежандра вычисляют по формуле:

(1.21)

Преимущество обобщенных рядов Фурье состоит не только в том, что они применяются при моделировании сложных непериодических процессов, но и в том, что для достижения достаточно хорошего приближения к исходной функции можно ограничиться малым числом слагаемых ряда m, то есть использовать полиномы низших порядков.

Точность моделирования определяется среднеквадратической погрешностью аппроксимации

(1.22)

Пользуясь выражениями (1.20), (1.21) и (1.12) запишем ряд Фурье - Лежандра для нашего дискретизированного сигнала X(ih)

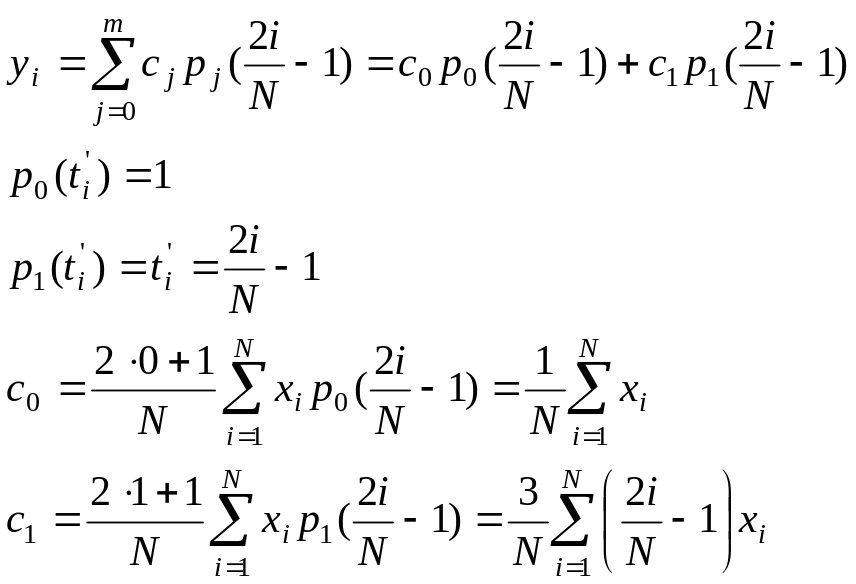
За x_i принимаем дискретизированный энергетический спектр сигнала

Тогда 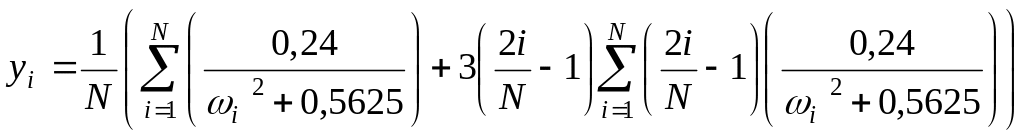(1.23)

Выражение (1.23) определяется количеством отсчетов N, которое напрямую связано с шагом дискретизации h и длительностью интервала наблюдения соотношением (1.18) . По условию, необходимо найти такой шаг дискретизации h, при котором среднеквадратическая погрешность аппроксимации (соотношение (1.22)) не превышала бы .

Для этого смоделируем выражение (1.23) и (1.22) в программе MathCAD с возможностью варьирования вышеуказанными параметрами:

Рассматривая энергетический спектр сигнала (рис.1), можно увидеть, что оба конца графика уходят в бесконечность, следовательно, при расчете шага дискретизации необходимо было подобрать такою длительность интервала наблюдения, чтобы среднеквадратическая погрешность аппроксимации не превышала порядка заданного значения. С помощью построенной модели было установлено, что при T=14000 порядок погрешности соответствует заданному. Далее с помощью той же модели был установлен оптимальный шаг дискретизации, при котором среднеквадратическая погрешность аппроксимации не превышает заданного значения, а дальнейшее уменьшение шага дискретизации не приводит к значительному уменьшению погрешности.

Таким образом, полученный шаг дискретизации равен при средней квадратической погрешности аппроксимации .

4. Нахождение значения коэффициента корреляции между сечениями сигнала, разделенными шагом дискретизации.

Коэффициент корреляции – мера статистической связи между случайными величинами, а в нашем случае между сечениями сигнала, разделенными шагом дискретизации. В п.1 была найдена корреляционная функция случайного сигнала X(t):

, в которой .

Коэффициент корреляции или нормированная корреляционная функция находится по формуле

(1.24)

Пользуясь выражением (1.24) найдем коэффициент корреляции между сечениями сигнала, разделенными шагом дискретизации

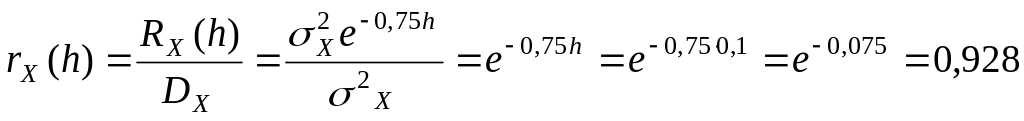
Такое значение коэффициента корреляции означает наличие сильной взаимосвязи между сечениями сигнала, разделенными шагом дискретизации.