3.5. Уравнение прямой

Каноническое уравнение прямой на плоскости имеет вид

, (3.19)

где произвольная точка на прямой, а координаты направляющего вектора (указывающего направленность прямой).

Уравнение прямой может быть записано в общем виде:

, или (3.20)

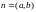
где – направляющий вектор, а  вектор нормали (направленный по перпендикуляру к прямой).

(3.20) называется общим уравнением прямой.

Если а  0, в  0, с  0, то прямая (3.20) пересекает обе координатные оси.

Если А =0, В 0, С  0, то прямая параллельна оси Ох.

Если А = 0, В  0, С = 0, то или у = 0 – уравнение оси Ох.

Если А  0, В = 0, С  0, то прямая или параллельна оси Оу.

Если А  0, В = 0, С = 0, то или х = 0 – уравнение оси Оу.

Если А  0, В  0, С = 0, то прямая проходит через начало координат.

Уравнение прямой, проходящей через две данные точки ( ; ) и ( ; )

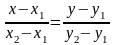(3.21)

Запишем это уравнение в виде (3.21.1)

Рассмотрим рис. 3.5, на котором изображено общее расположение прямой, проходящей через две данные точки и , и пересекающей обе оси координат. Угол  между положительным направлением оси Ох и прямой, взятый против часовой стрелки, называется углом наклона прямой. Тангенс угла наклона называется угловым коэффициентом прямой. Так как прямая параллельна оси Ох, то - прямоугольный и отношение

(3.22)

Тогда уравнение (3.22) можно записать и так

(3.23)

Это уравнение прямой, проходящей через данную точку в данном направлении (определяемом угловым коэффициентом k).

Пример 3.5. От продажи 200 шт. товара доход составляет 6000 руб., а от продажи 1000 шт. - 20000 руб. Учитывая линейность функции дохода (от объема продаж), определить доход от продажи 400 шт. товара.

Решение. Используя уравнение (3.21.1) и подставляя вместо координат точек (x₁;y₁), (x₂;y₂) координаты М₁(200; 6000), М₂(1000; 20000), получим:

, получим y = 17,5х +2500. Подставляя х = 400,

определим доход y = 9500 руб.

Если k величина не фиксированная, а переменная, то уравнение (3.23) называется уравнением пучка прямых, проходящих через данную точку.

Раскрывая скобки, получим

Обозначим величину , то уравнение запишется в виде

(3.24)

Это уравнение прямой с угловым коэффициентом.

При х = 0 - это отрезок, отсекаемый прямой на оси ординат, считая от начала координат, число k характеризует направление прямой, если k > 0, то угол наклона острый, а если k < 0, то угол наклона тупой.

Если k  0, b = 0, то прямая проходит через начало координат.

Если k = 0, b  0, то уравнение прямой, параллельной оси Ох.

В частности, если k = b = 0, то у = 0 – уравнение оси Ох.

Уравнение вид есть уравнение прямой, параллельной оси Оу. В частности, - уравнение оси Оу.

Пусть в общем уравнении прямой все коэффициенты не равны нулю. Запишем в виде и разделим на –С  0. Получим или . Обозначив , , получим:

(3.25)

Это уравнение прямой в отрезках. Здесь - отрезки отсекаемые прямой соответственно на осях Ох и Оу, считая от начала координат.

Например, прямая отсекает на осях отрезки х = -2, у = 5.

3.6. Длина отрезка и деление отрезка в данном отношении

Формула деления отрезка пополам:

если задан отрезок , и координаты точек , известны, то серединой отрезка является точка

.

Разделить данный отрезок в заданном отношении.

Пусть в R³ дан отрезок прямой (рис. 3.6.), координаты концов которого известны: , . Пусть - делящая точка с переменными координатами и заданное отношение, в котором точка М делит отрезок . Надо найти координаты делящей точки М.

Р ешим задачу в векторном виде. Проведем векторы , соединяющие начало координат О с точками . Рассмотрим векторы и . Они коллинеарны, так как лежат на одной прямой и = .

Но = , = или . Из равенства этих векторов следует пропорциональность соответствующих координат, то есть

, , .

Из этих трех равенств находим искомые координаты х, у, z делящей точки М:

, , (2.26)

В частности, если точка М делит отрезок пополам, то , =1, и координаты середины отрезка находим по формулам

, , (3.27)

3.7. Угол между двумя прямыми на плоскости

Если прямые заданы общими уравнениями и , то угол между ними такой же, как угол между нормальными векторами и прямых и находится по формуле, аналогичной формуле (3.13)

(3.28)

условие перпендикулярности: и параллельности: .

Угол между прямимы и можно найти по формуле

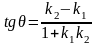. (3.29)

Условие перпендикулярности , условие параллельности .

Если речь идет об угле между двумя прямыми и не указан порядок, в котором они рассматриваются, то можно устанавливать этот порядок произвольно. Очевидно, что изменение порядка повлечет за собой изменение знака тангенса угла.